poj-1330(暴力写的lca)

传送门

一看就是lca的板子题

然而

（写这个的时候我忘了怎么写lca）

于是我就试着写暴力了

本以为会tle结果e了一次后居然a掉了

开心到起飞.嘿嘿嘿

但还是格式输出错误了一次而且在ce之前也de了一会儿（sdqxt太蒻了）

sd错误如下：

1. 边的编号和点的编号弄混了

2. 一开始直接写成i <= deep[x] – deep[y]

　于是导致循环少了好几次

　（这个问题我在博客了写了好多遍，可我还是错qwq..）

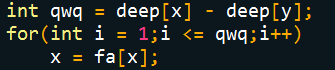
3. 但我真正提交的错误是，\n被我写成'空格'了（纯是没在意这事啊）

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;

int fa[],deep[],head[],nxt[],to[],cnt;
bool vis[];

inline int read()
{
    int sum = ,p = ;
    char ch = getchar();
    while(ch < '' || ch > '')
    {
        if(ch == '-')
            p = -;
        ch = getchar();
    }
    while(ch >= '' && ch <= '')
    {
        (sum *= ) += ch - '';
        ch = getchar();
    }
    return sum * p;
}

void dfs(int o)
{
    for(int i = head[o];i;i = nxt[i])
    {
        deep[to[i]] = deep[o] + ;
        dfs(to[i]);
    }
}

void add(int x,int y)
{
    fa[y] = x;
    nxt[++cnt] = head[x];
    head[x] = cnt;
    to[cnt] = y;
}

void llca(int x,int y)
{
    if(deep[x] < deep[y])//始终让x为最深的
        swap(x,y);
    int qwq = deep[x] - deep[y];
    for(int i = ;i <= qwq;i++)
        x = fa[x];
    if(x == y)
        printf("%d\n",y);
    else
    {
        while(x != y)
        {
            x = fa[x];
            y = fa[y];
        }
        printf("%d\n",y);
    }
}

int main()
{
    int t,n;
    t = read();
    while(t--)
    {
        n = read();
        cnt = ;
        memset(fa,,sizeof(fa));
        memset(deep,,sizeof(deep));
        memset(head,,sizeof(head));
        memset(nxt,,sizeof(nxt));
        memset(vis,,sizeof(vis));
        memset(to,,sizeof(to));
        for(int i = ;i < n;i++)
        {
            int a= read(),b = read();
            vis[b] = true;
            add(a,b);
        }
        int c = read(),d = read();
        for(int i = ;i <= n;i++)//找根节点
            if(!vis[i])
            {
                deep[i] = ;
                fa[i] = i;
                dfs(i);
                break;
            }
        llca(c,d);
    }
    return ;
}