Tri Tiling（hdu1143）

Tri Tiling

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 2731    Accepted Submission(s): 1547

Problem Description

In how many ways can you tile a 3xn rectangle with 2x1 dominoes? Here is a sample tiling of a 3x12 rectangle.

 

Input

Input consists of several test cases followed by a line containing -1. Each test case is a line containing an integer 0 ≤ n ≤ 30. 

 

Output

For each test case, output one integer number giving the number of possible tilings. 

 

Sample Input

2

8

12

-1

 

Sample Output

3

153

2131

 

 

Source

University of Waterloo Local Contest 2005.09.24

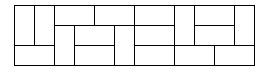
思路：

1.标记和概念说明
     f(n):其中的n即为题目中矩形的长，高固定位3，也即为题目中说的3xn中的n，f(n)表示当长为n时，
          所有的摆放方式的数量。
    分割线:一条竖直的线，这条线穿过题目中的矩形，将矩形一分为二，且这条线不能从砖的中间穿过，也
          就是说只有砖的边缘对齐的时候，才能穿过。
2.解题思想
2.1 对于每一种砖的摆放情况，可能有多条上面说的分割线，但是对于每一种情况，我们只需要所有分割线中
    最右边的一条，我们记为L。也就是说在L的右边的部分就是不可分割的了，但是左边可能还是可以分割
    的。对于L的左边我们继续使用函数f即可，而右边是需要我们研究的主要部分，因为右边不能应用函数f。

2.2 不能应用函数f的原因是因为右边不在可分割。对于长度为2的不可分割矩形的摆放方式有三种方式，对长
    度大于2的不可分割矩形的摆放方式有两种方式。上一句话的理解也许需要你拿起笔在纸上画一画。

2.3 同时，考虑这样的L可能在哪些位置？可能在从右边数起的长度为2的位置，也有可能在长度为4的位置，……，
    也有可能在长度为n的位置。当然，也只可能在上述的位置中，因此有如下结果：
        f(n)=f(n-2)*3+f(n-4)*2+...+f(2)*2+f(0)*2  ----  表达式1
    然后，将上式用n-2替换得：
        f(n-2)=f(n-4)*3+f(n-6)*2+...+f(2)*2+f(0)*2  ----  表达式2
    表达式1减去表达式2得：
        f(n)=4*f(n-2)-f(n-4)

2.4 在利用上面的递推公式时，我们需要两个递推的出口，即f(0) = 1, f(2) = 3.由上面的递推公式也知道
    不涉及当n为奇数的情况，当n为奇数时，直接为零。因为当n为奇数时，矩形的面积为奇数，但是不管我们使
    用了多少块砖，砖的总面积一定是个偶数，所以不存在任何的摆放形式。

转载请注明出处：寻找&星空の孩子 

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=1143

这里有一点我觉得比较坑。那就是F[0]=1;当n=0的时候为什么是1 ？？？

#include<stdio.h>
#define LL __int64
LL ans[35];
void init()
{
    ans[0]=1;
    ans[1]=ans[3]=0;
    ans[2]=3;ans[4]=11;
    for(int i=5;i<=30;i++)
    {
        if(i&1) ans[i]=0;
        else ans[i]=ans[i-2]*4-ans[i-4];
    }
}
int main()
{
    int n;
    init();
    while(scanf("%d",&n)!=EOF)
    {
        if(n==-1) break;
        printf("%I64d\n",ans[n]);
    }
    return 0;
}