内部排序->插入排序->希尔排序

文字描述

　　希尔排序又称缩小增量排序，也属于插入排序类，但在时间效率上较之前的插入排序有较大的改进。

　　从之前的直接插入排序的分析得知，时间复杂度为n*n， 有如下两个特点：

　　(1)如果待排序记录本身就是“正序”时， 其时间复杂度可减少为n。

　　(2)当待排序记录数很小时，直接插入排序的效率也比较高;

　　希尔排序正是从这两点分析出发对直接插入排序进行了改进。它的基本思想是：先将整个待排记录序列分割成为若干个子序列分别进行直接插入排序，待整个序列中的记录“基本有序“时，再对全体记录进行一次直接插入排序。

示意图

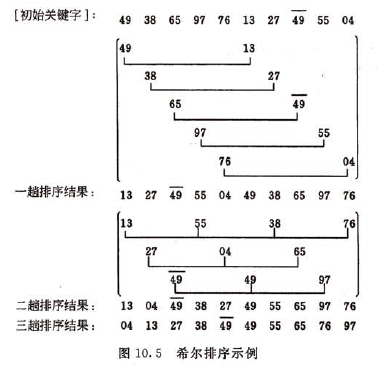
算法分析

　　希尔排序的空间复杂度是所取增量数组的个数加1。

　　希尔排序的时间复杂度分析是一个复杂的问题，因为它的时间是所取”增量”序列的函数，这涉及一些数学上尚未解决的难题。但是在大量的前人做的实验基础上推出：当n在某个特定范围内，希尔排序所需的比较和移动次数均约为n^(1.3)， 当n无穷大时，可减少到n(log₂n)^2。

　　增量序列可以有各种取法，但是需注意：应使增量序列中的值没有除1之外的公因子，并且最后一个增量值必须等于1。

　　希尔排序是不稳定的

代码实现

 #include <stdio.h>
 #include <stdlib.h>

 #define DEBUG

 #define EQ(a, b) ((a) == (b))
 #define LT(a, b) ((a) <  (b))
 #define LQ(a, b) ((a) <= (b))

 #define MAXSIZE 20
 typedef int KeyType;
 typedef int InfoType;
 typedef struct{
     KeyType key;
     InfoType otherinfo;
 }RedType;

 typedef struct{
     RedType r[MAXSIZE+];
     int length;
 }SqList;

 //依次打印顺序表L中的下标和关键字
 void PrintList(SqList L){
     int i = ;
     printf("下标值：");
     for(i=; i<=L.length; i++){
         printf("[%d] ", i);
     }
     printf("\n关键字：");
     for(i=; i<=L.length; i++){
         printf(" %-3d", L.r[i].key);
     }
     printf("\n其他值：");
     for(i=; i<=L.length; i++){
         printf(" %-3c", L.r[i].otherinfo);
     }
     printf("\n\n");
     return ;
 }

 /*
  *对顺序表L作一趟希尔插入排序。本算法和一趟直接插入
  *排序相比，作了以下修改：
  * 1。前后记录位置的增量为dk， 而不是1
  * 2。r[0]只是暂存单元，不是哨兵
  */
 void ShellInsert(SqList *L, int dk)
 {
     int i = , j = ;
     for(i=dk+; i<=L->length; ++i){
         //需将L->r[i]插入有序增量子表
         if(LT(L->r[i].key, L->r[i-dk].key)){
             //暂存在L->r[0]
             L->r[] = L->r[i];
             for(j=i-dk; j>&&LT(L->r[].key, L->r[j].key); j-=dk){
                 //记录后移，找插入位置
                 L->r[j+dk] = L->r[j];
             }
             //插入位置找到，插入数据
             L->r[j+dk] = L->r[];
         }
     }
 }

 //按照增量序列dlta[0..t-1]对顺序表L作希尔排序
 void ShellSort(SqList *L, int dlta[], int t)
 {
 #ifdef DEBUG
     printf("输入数组：\n");
     PrintList(*L);
 #endif
     int k = ;
     for(k=; k<t; k++){
         //一趟增量为dlta[k]的插入排序
         ShellInsert(L, dlta[k]);
 #ifdef DEBUG
         printf("第%d趟增量%d希尔排序后:\n", k, dlta[k]);
         PrintList(*L);
 #endif
     }
 }

 int  main(int argc, char *argv[])
 {
     if(argc < ){
         return -;
     }
     SqList L;
     int i = ;
     for(i=; i<argc; i++){
         if(i>MAXSIZE)
             break;
         L.r[i].key = atoi(argv[i]);
         L.r[i].otherinfo = 'a'+i-;
     }
     L.length = (i-);
     L.r[].key = ;
     L.r[].otherinfo = '';
     //希尔排序的增量 依次取9 5 3 1
     int dlta[] = {,,,};
     //调用希尔排序算法
     ShellSort(&L, dlta, );
     return ;
 }

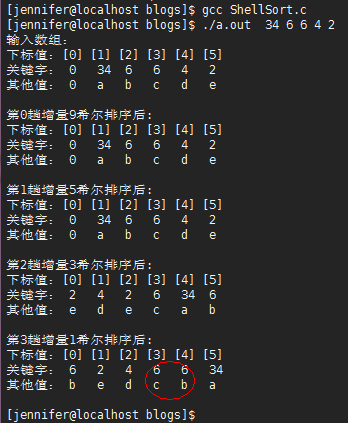
希尔排序

运行