对偶图 && 【BZOJ】1001: [BeiJing2006]狼抓兔子（对偶图+最短路）

http://www.lydsy.com/JudgeOnline/problem.php?id=1001

可谓惨不忍睹，一下午就在调这题了。

很久以前看到这题是一眼最大流，看到n<=1000，我也不管，我本着锻炼代码能力超时就超时的思想先写了个最大流，TLE是很正常的。。

直到今天下午，我看了题解，原来是转换成对偶图跑最短路，恩，很巧妙的思想。（论文周冬《两极相通——浅析最大—最小定理在信息学竞赛中的应用》）

首先介绍平面图：

定义：图中的一个点为源点s，另外一个点为汇点t，且s和t都在图中的无界面的边界上，我们称这样的平面图为s-t平面图。
性质：

（欧拉公式）如果一个连通的平面图有n个点，m条边和f个面，那么f=m-n+2
每个平面图G都有一个与其对偶的平面图G*
对偶图：G*中的每个点对应G中的一个面；对于G中的每条边e，e属于两个面f1、f2，加入边(f1*， f2*)
G的面数等于G*的点数，G*的点数等于G的面数
G与G*边数相同，G*中的环对应G中的割一一对应

举例（图中可能有错误，我指出来了）：

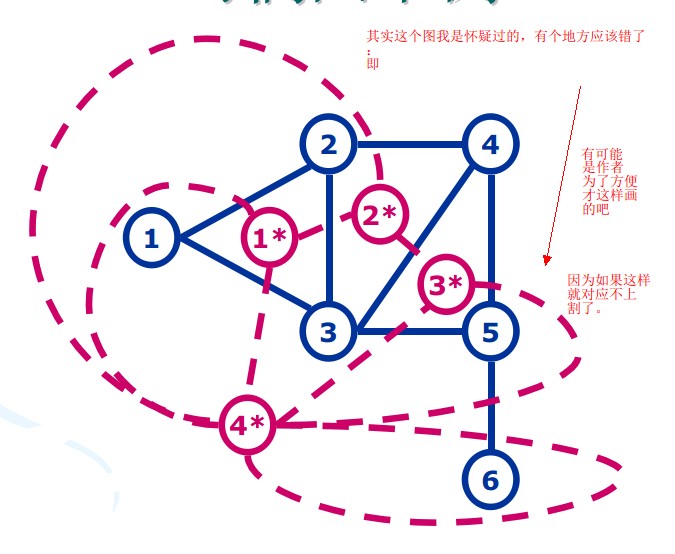
根据它的性质，这些环对应的就是一个割，那么我们只要找一个“最短的”环，那么就找到最小割了～最大流也找到了。

跑一次最短路即可，spfa是O(km)k可看作常数（upd：我sb，O(km)是发论文那个人乱说的。。。。），那么时间就大大减小。（你用dij作到nlgn我也没话说，反正spfa能过，你快点就快点。。）

那么如何建模呢？

我们将s和t连起来（自己画图连就行，实际操作不需要，能区分开来就行了），那么这个附加面我们设为s*，附加面外也就是无界面我们设为t*，按上面的方法连弧，跑一次s*到t*的最短路就行。

回到题目上来，此题变态，所以出现了一下TLE，一下RE，一下MLE，，，各种调试。。。各种静态查错。。好不容易a了。

ps：本题注意链的情况，即n==1或者m==1，那么面只有一个，即无界面，除非有特殊的技巧～不用特判，其实也就是当i=1或者j=1的时候，s和t在 “不存在的三角形”的编号内了，即s和t连接起来了，不会使得没有边连到s或者没有边连到t导致错误。

（此题空间跪了，我没有自己算，全看标程怎么给的空间了，。，）

#include <cstdio>

#include <cstring>

#include <string>

#include <iostream>

#include <cmath>

#include <algorithm>

using namespace std;

#define for1(i,a,n) for(i=a;i<=n;++i)

#define for2(i,a,n) for(i=a;i<n;++i)

#define for3(i,a,n) for(i=a;i>=n;--i)

#define for4(i,a,n) for(i=a;i>n;--i)

#define CC(i,a) memset(i,a,sizeof(i))

#define max(a,b) ((a)>(b)?(a):(b))

#define min(a,b) ((a)<(b)?(a):(b))

#define read(a) scanf("%d", &a)

#define print(a) printf("%d", a)

const int N=(999*999*2+2+10), M=N*3, oo=1000000000;

int ihead[N], inext[M], to[M], w[M], cnt;

int vis[N], q[M*2], front, tail, d[M], m;

inline int num(const int &i, const int &j) {

    return ((m-1)*(i-1)<<1)+(j<<1)-1;

}

inline int getnum() {

    int ret=0; char c;

    for(c=getchar(); c<'0' || c>'9'; c=getchar());

    for(; c>='0' && c<='9'; c=getchar()) ret=ret*10+c-'0';

    return ret;

}

inline void add(int u, int v, int c) {

    inext[++cnt]=ihead[u]; ihead[u]=cnt; to[cnt]=v; w[cnt]=c;

    inext[++cnt]=ihead[v]; ihead[v]=cnt; to[cnt]=u; w[cnt]=c;

}

inline int spfa(int s, int t, int n) {

    CC(vis, 0);

    int u, i;

    for1(i, 0, n) d[i]=oo;

    vis[s]=1; front=tail=d[s]=0;

    q[tail++]=s;

    while(front<tail) {

        u=q[front++]; if(front==(M<<1)-10) front=0;

        for(i=ihead[u]; i; i=inext[i]) if(d[to[i]]>d[u]+w[i]) {

            d[to[i]]=d[u]+w[i];

            if(!vis[to[i]]) {

                vis[to[i]]=1, q[tail++]=to[i];

                if(tail==(M<<1)-10) tail=0;

            }

        }

        vis[u]=0;

    }

    return d[t];

}

int main() {

    int n;

    n=getnum(); m=getnum();

    int i, j, c;

    int s=(n-1)*(m-1)*2+1, t=s+1;

    for1(i, 1, n) for2(j, 1, m) {

        c=getnum();

        if(i==1) add(num(i, j)+1, s, c);

        else if(i==n) add(num(i-1, j), t, c);

        else add(num(i, j)+1, num(i-1, j), c);

    }

    for2(i, 1, n) for1(j, 1, m) {

        c=getnum();

        if(j==1) add(num(i, j), t, c);

        else if(j==m) add(num(i, j-1)+1, s, c);

        else add(num(i, j), num(i, j)-1, c);

    }

    for2(i, 1, n) for2(j, 1, m) {

        c=getnum();

        add(num(i, j), num(i, j)+1, c);

    }

    print(spfa(s, t, t+1));

    printf("\n");

    return 0;

}

Description

现在小朋友们最喜欢的"喜羊羊与灰太狼",话说灰太狼抓羊不到，但抓兔子还是比较在行的，而且现在的兔子还比较笨，它们只有两个窝，现在你做为狼王，面对下面这样一个网格的地形：左上角点为(1,1),右下角点为(N,M)(上图中N=4,M=5).有以下三种类型的道路 1:(x,y)<==>(x+1,y) 2:(x,y)<==>(x,y+1) 3:(x,y)<==>(x+1,y+1) 道路上的权值表示这条路上最多能够通过的兔子数，道路是无向的. 左上角和右下角为兔子的两个窝，开始时所有的兔子都聚集在左上角(1,1)的窝里，现在它们要跑到右下解(N,M)的窝中去，狼王开始伏击这些兔子.当然为了保险起见，如果一条道路上最多通过的兔子数为K，狼王需要安排同样数量的K只狼，才能完全封锁这条道路，你需要帮助狼王安排一个伏击方案，使得在将兔子一网打尽的前提下，参与的狼的数量要最小。因为狼还要去找喜羊羊麻烦.

Input

第一行为N,M.表示网格的大小，N,M均小于等于1000.接下来分三部分第一部分共N行，每行M-1个数，表示横向道路的权值. 第二部分共N-1行，每行M个数，表示纵向道路的权值. 第三部分共N-1行，每行M-1个数，表示斜向道路的权值. 输入文件保证不超过10M

Output

输出一个整数，表示参与伏击的狼的最小数量.

Sample Input

3 4
5 6 4
4 3 1
7 5 3
5 6 7 8
8 7 6 5
5 5 5
6 6 6

Sample Output

HINT

Source