【codeforces div3】【E. Cyclic Components】

E. Cyclic Components

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You are given an undirected graph consisting of nn vertices and mm edges. Your task is to find the number of connected components which are cycles.

Here are some definitions of graph theory.

An undirected graph consists of two sets: set of nodes (called vertices) and set of edges. Each edge connects a pair of vertices. All edges are bidirectional (i.e. if a vertex aa is connected with a vertex bb, a vertex bb is also connected with a vertex aa). An edge can't connect vertex with itself, there is at most one edge between a pair of vertices.

Two vertices uu and vv belong to the same connected component if and only if there is at least one path along edges connecting uu and vv.

A connected component is a cycle if and only if its vertices can be reordered in such a way that:

• the first vertex is connected with the second vertex by an edge,
• the second vertex is connected with the third vertex by an edge,
• ...
• the last vertex is connected with the first vertex by an edge,
• all the described edges of a cycle are distinct.

A cycle doesn't contain any other edges except described above. By definition any cycle contains three or more vertices.

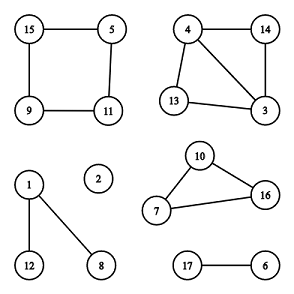
There are 66 connected components, 22 of them are cycles: [7,10,16][7,10,16] and [5,11,9,15][5,11,9,15].

Input

The first line contains two integer numbers nn and mm (1≤n≤2⋅1051≤n≤2⋅105, 0≤m≤2⋅1050≤m≤2⋅105) — number of vertices and edges.

The following mm lines contains edges: edge ii is given as a pair of vertices vivi, uiui (1≤vi,ui≤n1≤vi,ui≤n, ui≠viui≠vi). There is no multiple edges in the given graph, i.e. for each pair (vi,uivi,ui) there no other pairs (vi,uivi,ui) and (ui,viui,vi) in the list of edges.

Output

Print one integer — the number of connected components which are also cycles.

Examples

input

Copy

5 4
1 2
3 4
5 4
3 5

output

Copy

1

input

Copy

17 15
1 8
1 12
5 11
11 9
9 15
15 5
4 13
3 13
4 3
10 16
7 10
16 7
14 3
14 4
17 6

output

Copy

2

Note

In the first example only component [3,4,5][3,4,5] is also a cycle.

The illustration above corresponds to the second example.

题目大意：求单圈环的个数【单圈环就是只有一个圈的环...】

题目分析：观察单圈环的可以发现它的一个性质每个点的度都是2，所以

【方法一】只需要用dfs遍历一下所有连在一起点，查看点的度是不是为2

 #include <bits/stdc++.h>
 using namespace std;

 #define f first
 #define s second
 #define ll long long
 const int maxn=3e5;
 vector<int>v[maxn];
 int vis[maxn];
 int ans,flag;
 void dfs(int now,int fa)
 {
     vis[now]=;
     if(v[now].size()!=)flag=;
     for(auto i:v[now])
     {
     if(i==fa||vis[i])continue;
     dfs(i,now);
     }
 }

 int main()
 {
     int n,m;
     cin>>n>>m;
     for(int i=;i<m;i++)
     {
     int x,y;
     cin>>x>>y;

     v[x].push_back(y);
     v[y].push_back(x);
     }
     for(int i=;i<=n;i++)
     {
     flag=;
     int ok=;
     if(!vis[i])dfs(i,-),ok=;
     if(flag==&&ok==)ans++;
     }
     cout<<ans;
     return ;
 }

【方法二】

方法一中的dfs仅仅是寻找连在一起的点，其实寻找一个连通块连在一起的点只需要使用并查集就能解决，以下是并查集+判断度是不是为2

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<vector>
 using namespace std;
 const int maxn=;
 int fa[maxn];
 vector<int>qwq[maxn];
 vector<int>orz[maxn];
 int find(int x)
 {
     int xx=x;
     while(x!=fa[x])
     {
         x=fa[x];
     }
     while(fa[xx]!=x)
     {
         int t=fa[xx];
         fa[xx]=x;
         xx=t;
     }
     return x;
 }
 int main()
 {
     int n,k;
     scanf("%d%d",&n,&k);
     for(int i =  ; i <= n  ;i++)
     fa[i]=i;
     while(k--)
     {
         int a,b;
         scanf("%d%d",&a,&b);
         qwq[a].push_back(b);
         qwq[b].push_back(a);
         int qaq1=find(a);
         int qaq2=find(b);
         if(qaq1!=qaq2);
         fa[qaq1]=qaq2;
     }
     for(int i  =  ; i <= n  ; i++)
     {
         orz[find(i)].push_back(i);//利用连通块所有点的祖先来将联通块内部的点存在一起
     }
     int cnt=;
     for(int i =  ; i <= n ; i++)
     {
         if(orz[i].size()>)
         {
             bool or2=;
             for(int j =  ; j < orz[i].size()&&or2;j++)
             {
                 if(qwq[orz[i][j]].size()!=)or2=;
             }
             if(or2)cnt++;
         }
     }
     printf("%d\n",cnt);
     return ;
 }