Educational Codeforces Round 57题解

A.Find Divisible

沙比题

显然l和2*l可以直接满足条件。

代码

#include<iostream>
#include<cctype>
#include<cstdio>
#include<cstring>
#include<string>
#include<cmath>
#include<ctime>
#include<cstdlib>
#include<algorithm>
#define N 110000
#define L 100000
#define eps 1e-7
#define inf 1e9+7
#define db double
#define ll long long
#define ldb long double
using namespace std;
inline ll read()
{
	char ch=0;
	ll x=0,flag=1;
	while(!isdigit(ch)){ch=getchar();if(ch=='-')flag=-1;}
	while(isdigit(ch)){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();}
	return x*flag;
}
int main()
{
	ll t=read();
	for(ll i=1;i<=t;i++)
	{
		ll l=read(),r=read();
		cout<<l<<" "<<2*l<<endl;
	}
	return 0;
}

B.Substring Removal

细节题

分类讨论一下

先看一下是否整个字符串为同一种字符，此时答案为子串个数，特判掉。

如果不满足，则求出最长的前、后缀满足字符相等。

分别设为a，b。

ans=1+a+b+a*b（1为删除整个串的情况）

代码

#include<iostream>
#include<cctype>
#include<cstdio>
#include<cstring>
#include<string>
#include<cmath>
#include<ctime>
#include<cstdlib>
#include<algorithm>
#define N 1100000
#define L 1000000
#define eps 1e-7
#define inf 1e9+7
#define db double
#define ll long long
#define ldb long double
using namespace std;
inline ll read()
{
	char ch=0;
	ll x=0,flag=1;
	while(!isdigit(ch)){ch=getchar();if(ch=='-')flag=-1;}
	while(isdigit(ch)){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();}
	return x*flag;
}
const ll mo=998244353;
char s[N];
int main()
{
	ll n=read(),a=0,b=0,ans=1;
	scanf("%s",s+1);if(n==1){printf("1");return 0;}
	a=1;while(a<n&&s[a]==s[a+1])a++;ans+=a;
	b=n;while(b>1&&s[b]==s[b-1])b--;ans+=n-b+1;
	if(a==n&&b==1){cout<<(((n*(n-1)/2))%mo);return 0;}
	if(s[1]==s[n])
	{
		ans=(ans+((a*(n-b+1))%mo))%mo;
		cout<<ans%mo;
		return 0;
	}
	else
	{
		cout<<ans%mo;
		return 0;
	}
	return 0;
}

C.Polygon for the Angle

数论题

首先可以发现



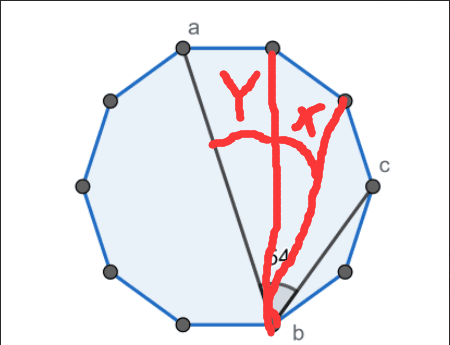
类似x和y这样的角是相等的。（可以构造外接圆，然后利用等弦对等角证明）

考虑计算这种角的大小

(n-2)*180/n是一个内角的大小，再除以n-2即为这种角的大小。

显然，n边形合法的条件是n/180|ang

当然可以直接数论强推。

这里讲一个简单的做法。

就是直接枚举n，强行判断一下即可。

需要注意的是，即使满足了整除这个条件，仍然有可能不合法。

比如第四个样例

query：178

answer：180

答案不是90的原因是90边形虽然满足了整除这个条件，但是最大的角也只有176°。

注意一下这个问题即可。

#include<iostream>
#include<cctype>
#include<cstdio>
#include<cstring>
#include<string>
#include<cmath>
#include<ctime>
#include<cstdlib>
#include<algorithm>
#define N 110000
#define L 100000
#define eps 1e-7
#define inf 1e9+7
#define db double
#define ll long long
#define ldb long double
using namespace std;
inline ll read()
{
	char ch=0;
	ll x=0,flag=1;
	while(!isdigit(ch)){ch=getchar();if(ch=='-')flag=-1;}
	while(isdigit(ch)){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();}
	return x*flag;
}
int main()
{
	ll t=read();
	for(ll o=1;o<=t;o++)
	{
		ll ang=read();
		bool flag=false;
		for(ll i=1;i<=400;i++)
		{
			ldb x=180.0/(ldb)i,k=(ldb)ang/x;
			if((180.0-x*2.0>=(ldb)ang)&&(fabs(k-(ll)k)<=0.0001||fabs(k-(ll)k)>=0.9999))
			{
				cout<<i<<endl;
				flag=true;break;
			}
		}
		if(!flag)printf("-1\n");
	}
	return 0;
}

D.Easy Problem

垃圾dp题

直接dp[i][j]表示放了i个数匹配hard匹配到了第j位。

每次决策有两种。

删除：代价ai，强制j保持不变。

不删除：无代价，j根据s[i]是否和j+1匹配来决定是否+1。

代码

#include<iostream>
#include<cctype>
#include<cstdio>
#include<cstring>
#include<string>
#include<cmath>
#include<ctime>
#include<cstdlib>
#include<algorithm>
#define N 150000
#define L 100000
#define eps 1e-7
#define inf 1e18+7
#define db double
#define ll long long
#define ldb long double
using namespace std;
inline ll read()
{
	char ch=0;
	ll x=0,flag=1;
	while(!isdigit(ch)){ch=getchar();if(ch=='-')flag=-1;}
	while(isdigit(ch)){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();}
	return x*flag;
}
ll n,a[N],dp[N][5];
char s[N],ch[5]={'0','h','a','r','d'};
ll dfs(ll x,ll k)
{
	if(x==n+1)return 0;
	if(dp[x][k]!=-1)return dp[x][k];
	dp[x][k]=inf;
	if(s[x]==ch[k+1])
	{
		if(k!=3)dp[x][k]=min(dp[x][k],dfs(x+1,k+1));
	}
	else dp[x][k]=min(dp[x][k],dfs(x+1,k));
	dp[x][k]=min(dp[x][k],dfs(x+1,k)+a[x]);
	return dp[x][k];
}
int main()
{
	n=read();scanf("%s",s+1);
	for(ll i=1;i<=n;i++)a[i]=read();
	memset(dp,-1,sizeof(dp));
	cout<<dfs(1,0);
	return 0;
}

E.The Top Scorer

组合，容斥，概率。

考虑枚举最大值和最大值的个数，分别设为o,i。

发现满足这个条件的方案数=c(n,i)f(n-i,s-io,o)

f(i,j,k)函数的意义是把和为j的数字分配给i个人，每个人的数字严格<k的方案数。

这个也就等价于sigema xi=j (xi<k)的解的个数。

这是一个经典的容斥题。

容斥的大体思路就是枚举至少有几个人的数值>=k（即不合法的个数）

用插板法去计算。

计算的复杂度为O(n)（n为人数个数）

考虑计算出来的方案数，对于有i个最大值的情况，每一种方案都有1/i的概率是第一个人获胜。

对总概率的贡献需要乘上一个1/i。

最终再除以一下总方案数即可（插板法计算）

代码

#include<iostream>
#include<cctype>
#include<cstdio>
#include<cstring>
#include<string>
#include<cmath>
#include<ctime>
#include<cstdlib>
#include<algorithm>
#define N 220000
#define L 200000
#define eps 1e-7
#define inf 1e9+7
#define db double
#define ll long long
#define ldb long double
using namespace std;
inline ll read()
{
	char ch=0;
	ll x=0,flag=1;
	while(!isdigit(ch)){ch=getchar();if(ch=='-')flag=-1;}
	while(isdigit(ch)){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();}
	return x*flag;
}
const ll mo=998244353;
ll ksm(ll x,ll k)
{
	ll ans=1;
	while(k)
	{
		if(k&1)ans=(ans*x)%mo;
		k>>=1;
		x=(x*x)%mo;
	}
	return ans;
}
ll fac[N],vac[N];
ll inv(ll x){return ksm(x,mo-2);}
ll c(ll n,ll m){return (fac[n]*((vac[m]*vac[n-m])%mo))%mo;}
int main()
{
	ll n=read(),s=read(),r=read(),ans=0;
	if(n==1){printf("1");return 0;}
	fac[0]=vac[0]=1;for(ll i=1;i<=L;i++)fac[i]=(fac[i-1]*i)%mo,vac[i]=(vac[i-1]*inv(i))%mo;
	for(ll o=r;o<=s;o++)for(ll i=1;i<=n&&i*o<=s;i++)
	{
		ll m=n-i,v=s-i*o,x=0;
		for(ll k=0,flag=1;k<=m&&v-k*o>=0;k++,flag=-flag)
		x=(x+flag*c(m,k)*c(v-k*o+m-1,m-1))%mo;
		if(!m&&!v)x=1;
		ans=(ans+((inv(i)*((c(n-1,i-1)*x)%mo))%mo))%mo;
	}
	ans=(ans*inv(c(s-r+n-1,n-1)))%mo;
	cout<<ans;
	return 0;
}

F.Inversion Expectation

概率，期望。

根据期望是线性函数这一性质，拆开算。

已知和已知的逆序对。

未知和未知的逆序对。

已知和未知的逆序对。

前两个都是非常好计算的。

计算第三个的时候。

考虑每一个已知的数字x。

设它左边有a个数未知，右边有b个数未知

再设共有k个比它小的数字未知。

显然这k个数相对x来说应该等概率分布。

左边期望有ka/(a+b)个，右边有kb/(a+b)个。

算一下即可。

G.Lucky Tickets

多项式模板题

发现题意就是让你先算出长度为n/2，和为k，（k<=n/2✖10）的方案数。

然后再乘法原理搞一搞。

考虑怎么计算和为k的方案数。

考虑暴力dp，用分治实现。

dp[n][k]=sigema dp[n/2][i]*dp[n/2][k-i]

（如果n为奇数，还需要再卷上一个dp[1]）

显然这是一个卷积的形式。

进一步的，发现这是一个多项式幂的形式。

直接分治+ntt即可。

代码

#include<iostream>
#include<cctype>
#include<cstdio>
#include<cstring>
#include<string>
#include<cmath>
#include<ctime>
#include<cstdlib>
#include<algorithm>
#define N 4400000
#define L 4000000
#define eps 1e-7
#define inf 1e9+7
#define ll long long
using namespace std;
inline int read()
{
    char ch=0;
    int x=0,flag=1;
    while(!isdigit(ch)){ch=getchar();if(ch=='-')flag=-1;}
    while(isdigit(ch)){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();}
    return x*flag;
}
const ll d=3,mo=998244353;
ll ksm(ll x,ll k)
{
    ll ans=1;
    while(k)
    {
        if(k&1)ans=(ans*x)%mo;
        k>>=1;
        x=(x*x)%mo;
    }
    return ans;
}
int rev[N];
void ntt(ll *f,int n,int flag)
{
    ll t,w,wn;
    int i,j,k,kk;
    for(i=0;i<n;i++)rev[i]=(rev[i>>1]>>1)+((i&1)*(n>>1));
    for(i=0;i<n;i++)if(i<rev[i])swap(f[i],f[rev[i]]);
    for(k=2,kk=1;k<=n;k<<=1,kk<<=1)
    {
        wn=ksm(d,(mo-1)/k);
        if(flag==-1)wn=ksm(wn,mo-2);
        for(i=0;i<n;i+=k)
        for(j=0,w=1;j<kk;j++,w=(w*wn)%mo)
        {
            t=(w*f[i+j+kk])%mo;
            f[i+j+kk]=(f[i+j]-t+mo)%mo;
            f[i+j]=(f[i+j]+t)%mo;
        }
    }
    if(flag==-1)
    {
        ll inv=ksm(n,mo-2);
        for(int i=0;i<n;i++)f[i]=(f[i]*inv)%mo;
    }
}
ll a[N],b[N],f[N],g[N];
void solve(int n)
{
	if(n==1)return;
	solve(n/2);
	int len;
	for(len=1;len<=n*10;len<<=1);for(int i=0;i<len;i++)a[i]=f[i];
	ntt(a,len,+1);for(int i=0;i<len;i++)a[i]=(a[i]*a[i])%mo;ntt(a,len,-1);
	for(int i=0;i<len;i++)f[i]=a[i];
	if(n&1)
	{
		for(len=1;len<=n*10;len<<=1);
		for(int i=0;i<len;i++)a[i]=f[i],b[i]=g[i];
		ntt(a,len,+1);ntt(b,len,+1);
		for(int i=0;i<len;i++)a[i]=(a[i]*b[i])%mo;
		ntt(a,len,-1);
		for(int i=0;i<len;i++)f[i]=a[i];
	}
}
int main()
{
    int n=read()/2,k=read(),x;
    for(int i=1;i<=k;i++)x=read(),f[x]=g[x]=1;
    solve(n);
    ll ans=0;
	for(int i=0;i<=n*10;i++)ans=(ans+((f[i]*f[i])%mo))%mo;
    cout<<ans;
    return 0;
}