complexity_action

大话数据结构

 /*
 顺序存储的结构
 */
 #define MAXSIZE 20
 //存储空间初始分配量
 typedef int ElemType;
 //ElemType类型根据实际情况而定，这里假设为int
 typedef struct {
     ElemType data[MAXSIZE];
 //    数组存储数据元素，最大值为MAXSIZE
     int length;
 //    线性表当前长度
 } SqList;
 /*
 地址计算方法 

 每个数据元素，不管是整形、实型、字符型，它们都要占用一定的存储单元。
 假设为c单元，那么线性表中第i个数据元素和第i+1个数据元素的存储位置满足
 下列关系（LOC表述获得存储位置的函数）：
 LOC(a_i_) = LOC(a_i-1_)+c
 (_表示下标的起始标志)
 LOC(a_i) = LOC(a_1_)+(i-1)*c

 计算线性表中任意位置的地址，时间相同。
 对每个线性表位置的存入或者取出数据，对于计算机而言，均为相等的时间，为一个常熟。
 时间复杂度
 存取时间性能
 O(1) 

 */

 /*
 顺序存储结构的插入与删除
 */ 

 /*获得元素的操作*/
 #define OK 1
 #define ERROR 0
 #define TRUE 1
 #define FALSE 0
 typedef int Status;
 //Status 是函数的类型，其值是函数结果状态码，如OK
 //初始条件：顺序线性表L已存在，1<=i<=ListLength(L)
 //操作结果：用e返回L中第i个数据元素的值
 Status GetElem(SqList L, int i, ElemType *e) {
     if(L.length== || i< || i>L.length)
         return ERROR;
     *e=L.data[i-];
     return OK;
 }
 //GetElem(L,i*e) 查 获得元素操作
 //时间复杂度O(1)

 /*
 插入操作
 */

 //ListInsert(*L,i,e) 增 添加元素操作
 //初始条件：顺序线性表L已存在，i<=i<=ListLength(L)
 //操作结果：在L中第i个位置之前插入新的数据元素e，L的长度增加1
 Status ListInsert(SqList *L, int i, ElemType e) {
     int k;//???improve下移？
     if(L->length==MAXSIZE)
     //顺序线性表已满
         return ERROR;
     if(L.length== || i< || i>L.length)
         return ERROR;
     if(i<=L->length) {
         for(k=L->length-; k>=i-; k--)
             L->data[k+] = L->data[k];
     }
     L->data[i-]=e;
     L->length++;
     return OK;
 }
 /*
 删除操作
 */

 //初始条件：同上
 //删除结果：删除L的第i个数据元素，并用e返回其值，L的长度减1
 Status ListDelete(SqList *L, int i, ElemType *e) {
     int k;
     if(L->length==)
     //线性表为空
         return ERROR;
     if(i< || i>L->length)
         return ERROR;
     *e = L->data[i-];
     if(i<L-length) {
         for(k=i; k<L->length; k++)
             L->data[k-]=L->data[k];
     }
     L->length--;
     return OK;
 }

 /*
 插入和删除的时间复杂度
 最好的情况：元素要插入到最后一个位置或者删除最后一个元素
             不需要移动元素
             O(1)
 最坏的情况：元素要插入到第一个位置或者删除第一个元素
             需要移动所有元素
             O(n)
 每个位置插入或删除呀元素的可能性相同
 平均复杂度
 O(n)
 */

线性表 linear list

n个数据元素的有限序列

线性链表：每个节点只包含一个指针域

循环链表 circular linked list

O(1)

将2个线性表合并成一个表，仅需将一个表的表尾和另一个表的表头相接：仅需改变2个指针值即可。

双向链表 double linked list

单链表 NextElem O(1)  PriorElem O(n)

NextElem O(1)  PriorElem O(1)

栈 stack 仅在表尾进行插入或删除操作的线性表

top bottom  栈顶 栈底

last in first out 后进先出

队列 queue first in first out

front rear 队头 队尾

tree 4

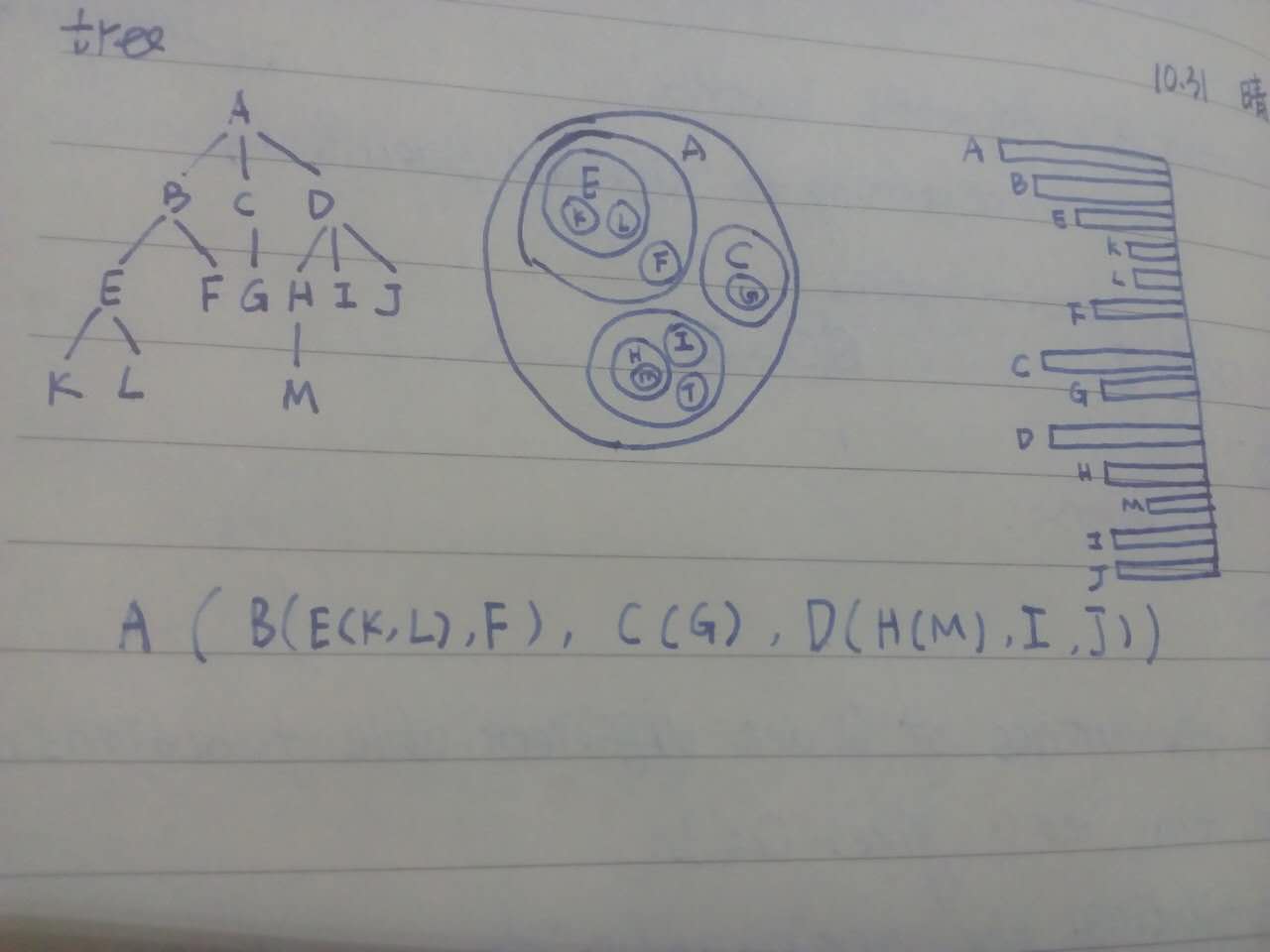
forest 互补相交的树的集合

binary tree

树中不存在度大于2的节点

满二叉树

一棵深度为k且有2^k-1个结点的二叉树