题目分享P

题意：

给出一棵n个节点的树，这棵树的每条边有一个权值，这个权值只可能是0或1。 在一局游戏开始时，会确定一个节点作为根。接下来从女生开始，双方轮流进行 操作。
当一方操作时，他们需要先选择一个不为根的点，满足该点到其父亲的边权为1; 然后找出这个点到根节点的简单路径，将路径上所有边的权值翻转（即0变成1，1 变成0 )。
当一方无法操作时(即所有边的边权均为0)，另一方就获得了胜利。
如果在双方均采用最优策略的情况下，女生会获胜，则输出“Girls win!”，否则输 出“Boys win!”。
为了让游戏更有趣味性，在每局之间可能会有修改边权的操作，而且每局游戏指 定的根节点也可能是不同的。
具体来说，修改边权和进行游戏的操作一共有m个，具体如下：
∙∙“0 x”表示询问对于当前的树，如果以x为根节点开始游戏，哪方会获得胜利。
∙∙“1 x y z ”表示将x和y之间的边的边权修改为z。

分析：

一道在树上的博弈论题

首先，我们先不管是否是最优策略，我们先就愣头青走憨憨走法——每次都走最深的这样一个节点，比如

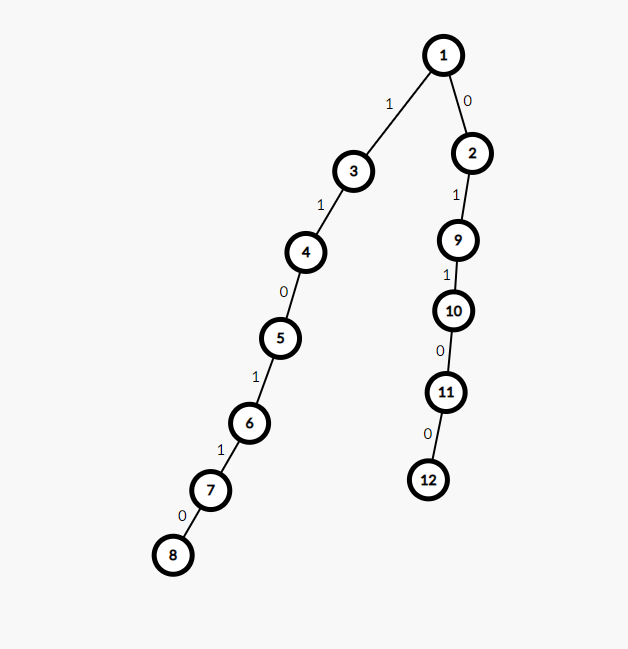
那么我们按照这个规则，先看左边那条链并先选7号节点

对了，这里其实还有一个小小的性质，每条链末尾的0一定是没用的，因为只有他后面的1才能使它翻转成1，而他是末尾的0

所以知道这个性质以及选完7号节点后，树就变成了这样子

然后就是5号节点

最后是4号节点

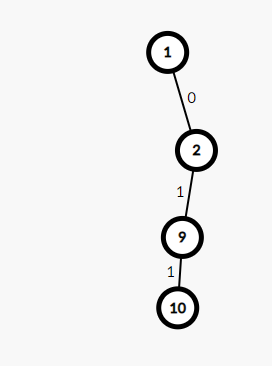
你会发现，假如只有这条链的话到这里已经决出胜负了

而且不难发现的是，在这种憨憨决策中，与根节点直接相连的那条边似乎非常的重要

因为假如我们将这条链划分一下肯定是一块全是1的链，一块全是0的链相间分布（显然）

那么我们这种憨憨走法第一步会将最后一块1的链吞掉，然后剩下的链翻转，你也可以理解为规则翻转，也就是说我们下次就要选0的那块了

以此类推，那么如果最后一块是1的话也就是说连接根节点的那条边是1，那么你就会走奇数步，而如果是0的话就会走偶数步

奇数步与偶数步也就对应了游戏的输赢（奇数对应女孩赢，偶数对应男孩赢）

当然，这种憨憨走法男主和女主显然不会这么走

比如

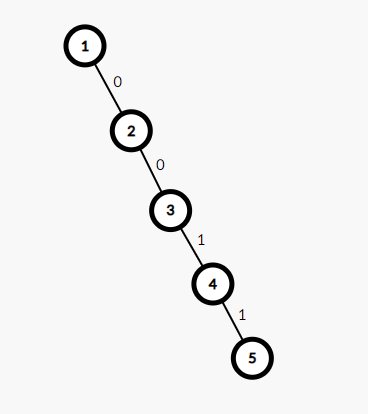
在憨憨走法的前提下，这显然是个男孩必赢的局，那女孩有什么能做的，她可不想输啊！

走5必输，那就走4吧

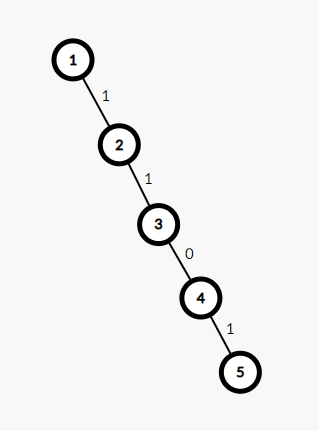
你会发现，之前的走法会让链的块数减一，而这次却让链的块数加一，但这时如果两人继续“憨憨”的话依然是男孩必赢，因为这次相当于男孩先手，而这次有奇数个块，显然男孩必赢

那么我们不难发现，如果我们即使突然“醒悟”，不憨了，但也难逃输的命运，而已经命中注定赢的那位，只需要一直憨下去就行了，当然他也可以皮一下，但就是输不了就很气

当然一条链是这样，更多的链显然也一定是这样，因为每条链都是“命中注定”，那么我们就可以把一颗树化简成一个根节点连着一些节点

因为每条链的结果只与他与根节点连接的那条边有关

原来一条复杂的树，现在只剩下一个“拖把头”，显然就很好做了，轮流取1就完事了，那么很容易得到，最后“拖把头”里1的个数是奇数就是女孩赢，偶数个就是男孩赢

最后就是这个题目中的修改操作以及换根查询了，修改我直接采用莽着改，的确有超时的风险，不过这题核心是想到这个转化，我觉得做数据的应该是做人的qaq

查询当然也是扫一遍他连着的所有边，具体如何实现，我相信你们都写的出来）：

代码：

#include<cstdio> #include<algorithm> #include<vector> using namespace std; const int maxn=4e4+1; struct Node { int pos,val; Node(){} Node(int POS,int VAL){pos=POS,val=VAL;} }; vector<Node> e[maxn]; int main() { int t,n,m,x,y,z,p; scanf("%d",&t); while(t--) { scanf("%d%d",&n,&m); for(int i=1;i<=n;i++)e[i].clear(); for(int i=1;i<n;i++) { scanf("%d%d%d",&x,&y,&z); e[x].push_back(Node(y,z)); e[y].push_back(Node(x,z)); } while(m--) { scanf("%d",&p); if(!p) { scanf("%d",&x); int ans=0; for(int i=0;i<e[x].size();i++) ans+=e[x][i].val; if(ans&1) printf("Girls win!\n"); else printf("Boys win!\n"); } else { scanf("%d%d%d",&x,&y,&z); for(int i=0;i<e[x].size();i++) { if(y==e[x][i].pos) { e[x][i].val=z; break; } } for(int i=0;i<e[y].size();i++) { if(x==e[y][i].pos) { e[y][i].val=z; break; } } } } } return 0; }

说实话我还真不知道咋展示代码[笑哭]

其实实现过程就是把每个节点连接的节点都用vector存一下，然后每次修改的时候就扫一遍，找到你想修改的那个点对应连的边，然后改就完事了