【贪心 哈夫曼树】bzoj2923: [Poi1998]The lightest language

失去了以前用STL乱搞的能力……

题目描述

语言也是数学上经常研究的一种数据。

给出数学上关于语言的如下定义：

• 字母表：大小为 K 的字母表是一个由 K 不同的字符组成的集合。
• 单词：长度为 m 的单词是以 m 个字母表中的字符组成的字符串。
• 语言：语言是由若干个单词组成的集合。
• 非前缀的：一种语言是非前缀的，当且仅当其中任意两个单词不存在前缀关系。

现在每个字母表中的字母有一个权值，单词的权值是单词中每个字母的权值和，语言的权值是单词的权值之和。

例如：

K=2，字母a权值为 2，字母b权值为 5，字符串aba权值为 9。

语言 {ab,aba,b} 不是非前缀的，而非前缀的语言 {aa,ab,b} 权值是 16。

给出n,K，每个字母的权值 Wi，求包含 n 个单词的非前缀语言中最小的权值是多少。

数据范围

对于 20% 的数据，n,K≤5

对于另 30% 的数据，wi=1

对于另 30% 的数据，K=2

对于所有数据，2≤n≤10000,2≤K≤26,1≤wi≤10000

时间限制 1s

空间限制 256 MB

---

题目分析

整个单词树可以看做trie的样子，

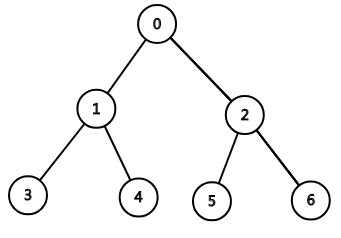
那么我的第一思路就是在这个tire上面树形dp……

既然要dp那么肯定要涉及到开数组空间的问题。

注意到若一层能够“铺满”所有n个节点，那么往下编码是一定不更优的。所以最大情况是补成一个满二叉树。

但是这个数据范围对于树上背包来说不对啊……

于是就活生生卡住一个小时。

回过头来看这个问题：非前缀；最小编码和……

这是个类哈夫曼树的问题啊。

与常规的哈夫曼问题不同，此题既然确定个数而加权不同，就可以从树根往下处理。

于是乎，这么一个贪心扩展的过程，就可以用multiset来维护……

最后STL的细节问题需要注意一下。

 #include<bits/stdc++.h>
 typedef long long ll;
 const int maxn = ;

 ll sum,ans;
 int n,k,w[maxn];
 std::multiset<ll> s;

 int read()
 {
     char ch = getchar();
     int num = ;
     bool fl = ;
     for (; !isdigit(ch); ch = getchar())
         if (ch=='-') fl = ;
     for (; isdigit(ch); ch = getchar())
         num = (num<<)+(num<<)+ch-;
     if (fl) num = -num;
     return num;
 }
 int main()
 {
     n = read(), k = read(), ans = 1ll<<;
     for (int i=; i<=k; i++)
         w[i] = read(), sum += w[i], s.insert(w[i]);
     for (ll cnt=sum; cnt<ans;)
     {
         if (s.size()==n){
             if (cnt < ans) ans = cnt;
             else break;
         }
         std::multiset<ll>::iterator p = s.begin();
         cnt += sum+(*p)*k;
         for (int i=; i<=k; i++)
             s.insert(w[i]+*p);
         cnt -= *p, s.erase(p);
37         while (s.size() > n)
38             cnt -= *s.rbegin(), s.erase(--s.end());
     }
     printf("%lld\n",ans);
     return ;
 }

END