【线性基】bzoj2322: [BeiJing2011]梦想封印

线性基的思维题+图常见套路

Description

渐渐地，Magic Land上的人们对那座岛屿上的各种现象有了深入的了解。

为了分析一种奇特的称为梦想封印（Fantasy Seal）的特技，需要引入如下的概念：

每一位魔法的使用者都有一个“魔法脉络”，它决定了可以使用的魔法的种类。

一般地，一个“魔法脉络”可以看作一个无向图，有N个结点及M条边，将结点编号为1~N，其中有一个结点是特殊的，称为核心（Kernel），记作1号结点。每一条边有一个固有（即生成之后再也不会发生变化的）权值，是一个不超过U的自然数。

每一次魔法驱动，可看作是由核心（Kernel）出发的一条有限长的道路（Walk），可以经过一条边多次，所驱动的魔法类型由以下方式给出：

将经过的每一条边的权值异或（xor）起来，得到s。

如果s是0，则驱动失败，否则将驱动编号为s的魔法（每一个正整数编号对应了唯一一个魔法）。

需要注意的是，如果经过了一条边多次，则每一次都要计入s中。

这样，魔法脉络决定了可使用魔法的类型，当然，由于魔法与其编号之间的关系尚未得到很好的认知，此时人们仅仅关注可使用魔法的种类数。

梦想封印可以看作是对“魔法脉络”的破坏：

该特技作用的结果是，“魔法脉络”中的一些边逐次地消失。

我们记总共消失了Q条边，按顺序依次为Dis1、Dis2、……、DisQ。

给定了以上信息，你要计算的是梦想封印作用过程中的效果，这可以用Q+1个自然数来描述：

Ans0为初始时可以使用魔法的数量。

Ans1为Dis1被破坏（即边被删去）后可以使用魔法的数量。

Ans2为Dis1及Dis2均被破坏后可使用魔法的数量。

……

AnsQ为Dis1、Dis2、……、DisQ全部被破坏后可以使用魔法的数量。

Input

第一行包含三个正整数N、M、Q。

接下来的M行，每行包含3个整数，Ai、Bi、Wi，表示一条权为Wi的与结点Ai、Bi关联的无向边，其中Wi是不超过U的自然数。

接下来Q行，每行一个整数：Disi。

Output

一共包Q+1行，依次为Ans0、Ans1、……、AnsQ。

HINT

【数据规模和约定】

所有数据保证该无向图不含重边、自环。

所有数据保证不会有一条边被删除多次，即对于不同i和j，有Disi≠Disj

30%的数据中N ≤ 50，M ≤ 50，Q ≤50，U≤100；

60%的数据中N ≤ 300，M ≤ 300，Q ≤50，U≤10^9；

80%的数据中N ≤ 300，M ≤ 5000，Q ≤5000，U≤10^18；

100%的数据中N ≤ 5000，M ≤ 20000，Q ≤20000，U≤10^18；

---

题目分析

这里线性基图上的问题和2115Xor一样，处理的技巧是把图做成dfs树和非树边。

题目所求的问题即：在一个无向图中，求以1为起点的非简单路径的种类数。

那么和上一题一样， $所有的非简单路径$  等价于  $一条简单路径$ + $若干个环$。而我们遇到的最主要问题在于，现在有两条路径，而它们各自和一些环异或之后，可能会存在结果相同的情况。整一个问题的瓶颈正是在于这一部分的去重。

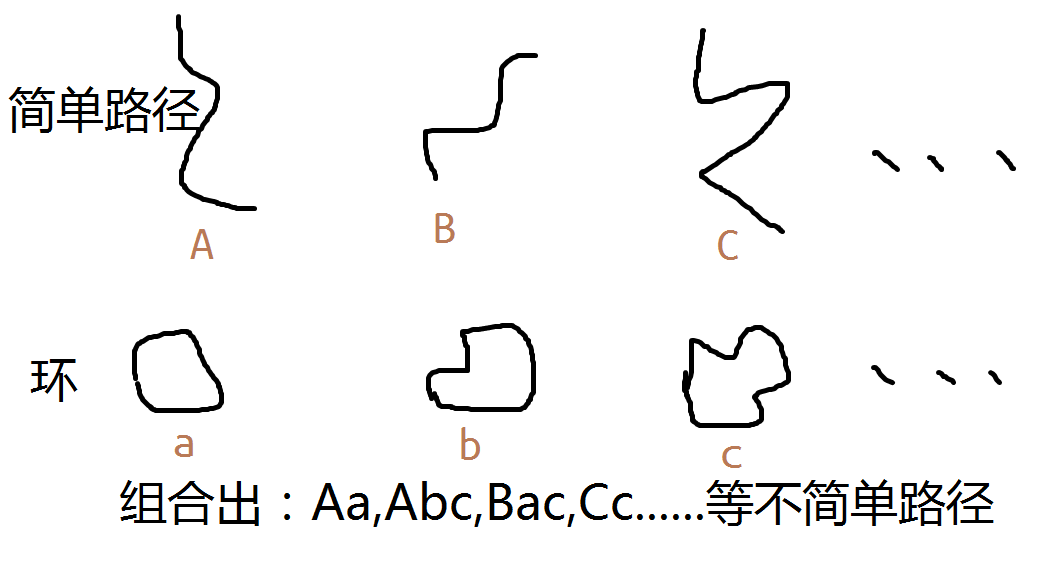
这里有一种巧妙的技巧，借鉴了最小表示的思想。

首先应该意识到，路径$A$和$B$如果存在各自异或$a$，$b$后数值相等的情况（即A xor a = B xor b），那么路径A,B实质上是等价的，因为它们的其他任何情况也必定是会相等的。

注意到线性基的性质：$（一条路径）异或（若干环）形成的值域集合$=$（一条路径先异或若干环）异或（若干环）形成的值域集合$（这里说得严谨一些就是张成相等）。那么，对于路径$A$,$B$，可以先用线性基内的环将它们“最小表示”一下，于是就保证了加进来的路径“本质不同”。

一个槽点：原数据如果不将$v[]$（存环的数组）从大到小排序，而直接按照插入顺序来“最小表示”，也能通过此题。

 #include<bits/stdc++.h>
 typedef long long ll;
 const int maxn = ;
 const int maxm = ;
 const int maxq = ;

 struct Edge
 {
     int u,v;
     ll val;
     Edge(int a=, int b=, ll c=):u(a),v(b),val(c) {}
 }edges[maxm],etmp[maxm];
 int n,m,q,del[maxq];
 int edgeTot,head[maxn],nxt[maxm];
 ll dis[maxn],p[],ans[maxq],tmp;
 bool tag[maxm];
 std::set<ll> s;
 std::set<ll>::iterator it;

 ll read()
 {
     char ch = getchar();
     ll num = , fl = ;
     for (; !isdigit(ch); ch = getchar())
         if (ch=='-') fl = -;
     for (; isdigit(ch); ch = getchar())
         num = (num<<)+(num<<)+ch-;
     return num*fl;
 }
 void addedge(int u, int v, ll c)
 {
     edges[++edgeTot] = Edge(u, v, c), nxt[edgeTot] = head[u], head[u] = edgeTot;
     edges[++edgeTot] = Edge(v, u, c), nxt[edgeTot] = head[v], head[v] = edgeTot;
 }
 ll calc(ll c)
 {
     for (int i=; i<=p[]; i++)
         if ((c^p[i]) < c) c ^= p[i];
     return c;
 }
 void update(ll c)
 {
     if (!c) return;
     for (it=s.begin(); it!=s.end(); it=s.upper_bound(tmp))
     {
         tmp = *it;
         if ((tmp^c) < tmp)
             s.erase(it), s.insert(tmp^c);
     }
     p[++p[]] = c;
     for (int j=p[]; j>=; j--)
         if (p[j] > p[j-]) std::swap(p[j], p[j-]);
         else break;
 }
 void dfs(int x, int fa, ll c)
 {
     dis[x] = c, tmp = calc(c);
     if (tmp&&(s.count(tmp)==)) s.insert(tmp);
     for (int i=head[x]; i!=-; i=nxt[i])
     {
         int v = edges[i].v;
         if (v!=fa){
             if (dis[v]==-) dfs(v, x, c^edges[i].val);
             else update(calc(dis[v]^c^edges[i].val));
         }
     }
 }
 void connect(int u, int v, ll c)
 {
     addedge(u, v, c);
     if (dis[u]!=-&&dis[v]!=-) update(calc(dis[u]^dis[v]^c));
     else{
         if (dis[u]==-&&dis[v]==-) return;
         if (dis[u]==-) dfs(u, v, dis[v]^c);
         else dfs(v, u, dis[u]^c);
     }
 }
 int main()
 {
     memset(dis, -, sizeof dis);
     memset(head, -, sizeof head);
     n = read(), m = read(), q = read(), dis[] = , s.insert();
     for (int i=; i<=m; i++)
         etmp[i].u = read(), etmp[i].v = read(), etmp[i].val = read();
     for (int i=; i<=q; i++) del[i] = read(), tag[del[i]] = ;
     for (int i=; i<=m; i++)
         if (!tag[i]) connect(etmp[i].u, etmp[i].v, etmp[i].val);
     ans[q+] = s.size()*(1ll<<p[])-;
     for (int i=q; i; i--)
     {
         connect(etmp[del[i]].u, etmp[del[i]].v, etmp[del[i]].val);
         ans[i] = s.size()*(1ll<<p[])-;
     }
     for (int i=; i<=q+; i++) printf("%lld\n",ans[i]);
     return ;
 }
 /*
 8 10 0
 8 4 5
 4 5 9
 7 1 5
 1 4 9
 2 8 1
 6 5 5
 8 3 6
 7 4 7
 7 3 6
 1 3 3
 */

END