gitblit-禁用用户
- 使用管理员账号(此处演示使用admin)登录到系统
- 右上角,找到用户菜单

- 再用户列表,找到要进行权限管理的用户,(演示alex)

- 禁用用户,取消权限
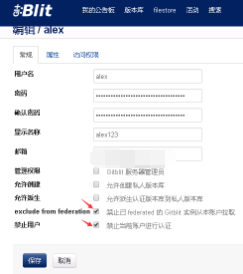
- 验证已经禁用

- pull 权限被禁止

gitblit-禁用用户的更多相关文章
- 查询oracle中所有用户信息 禁用用户
----查询oracle中所有用户信息 ----1.查询数据库中的表空间名称 ----1)查询所有表空间 select tablespace_name from dba_tablespaces; se ...
- win10 磁盘占用高--- 禁用用户改善反馈 CompatTelRunner.exe
1. 2.右键点开[这台电脑],点[管理],点[服务和应用程序]点[服务],在右边框里把[superfetch] [windows search][HomeGroupListener] [HomeGr ...
- Dyanmics CRM您无法登陆系统。原因可能是您的用户记录或所属的业务部门在Microoft Dynamics CRM中已被禁用
当在操作CRM时,做不论什么的写操作包含创建数据.更新数据.都会提示以下截图中的错误:"您无法登陆系统.原因可能是您的用户记录或所属的业务部门在Microoft Dynamics CRM中已 ...
- 禁用掉用户帐号,用户Lync客户端仍然可以登录!
问题: 有这样的一个情况,一位具有LYNC权限的用户离职了,AD账号已经禁用.LYNC和邮箱功能暂时保留.可用户离职4天了,还能够正常登录到LYNC,能够正常发送和接收即时消息.我经过测试,确实AD账 ...
- AD域 根据 用户属性userAccountControl 来判断用户禁用属性
参考:https://support.microsoft.com/zh-cn/help/305144/how-to-use-the-useraccountcontrol-flags-to-manipu ...
- 启用或禁用普通用户Exchange Online PowerShell功能
默认情况下,允许在 Microsoft 365 中创建的所有帐户都可以使用 Exchange Online PowerShell.管理员可以使用 Exchange Online PowerShell ...
- 在 Linux 上为特定的用户或用户组启用或禁用 SSH
由于你的公司标准规定,你可能只能允许部分人访问 Linux 系统.或者你可能只能够允许几个用户组中的用户访问 Linux 系统.那么如何实现这样的要求呢?最好的方法是什么呢?如何使用一个简单的方法去实 ...
- windows系统添加删除用户命令!
参考:net help usernet help group Net user添加或修改用户帐户或者显示用户帐户信息. 语法net user [UserName [Pa ...
- Linux学习笔记(12)用户和用户组管理
越是对服务器安全性要求高的服务器,越需要建立合理的用户权限等级制度和服务器操作规范.在Linux中主要是通过用户配置文件来查看和修改用户信息. 1 用户信息文件 (1)用户信息文件/etc/passw ...
- 【转】dsadd user批量创建AD用户命令详解
常见的批量创建用户的方法有四种: 一. 帐户模板的方式 二. CSVDE和LDIFDE 三. 脚本的方式 四. DSADD 但是很少有详细的资料使用DSADD的方式来批量创建帐户,那么我就把我近期使用 ...
随机推荐
- 使用LinQ进行增删改查
数据库访问技术: ADO.net EF框架 LinQ LinQ是一种高集成化的数据库访问技术,他将数据库中的表映射成程序中的类 数据库的表名变成类名 数据库的列名变成字段名/属性名 所有的操作都是通过 ...
- Java Hashtable详细介绍和使用示例
①对Hashtable有个整体认识 和HashMap一样,Hashtable 也是一个散列表,它存储的内容是键值对(key-value)映射.Hashtable 继承于Dictionary,实现了Ma ...
- ansible playbook基本操作
一.ansible playbook简单使用 相当于是把模块写入到配置文件里面 vim /etc/ansible/test.yml //写入如下内容: --- - hosts: 127.0.0.1 r ...
- 防止常见XSS 过滤 SQL注入 JAVA过滤器filter
XSS : 跨站脚本攻击(Cross Site Scripting),为不和层叠样式表(Cascading Style Sheets, CSS)的缩写混淆,故将跨站脚本攻击缩写为XSS.恶意攻击者往W ...
- GRUB2 分析 (四)
接上一篇 kernel.img由startup.S以及一堆c文件编译而成.这是一个ELF格式的文件.(其实前面的boot.img. diskboot.img.lzma_decompress.img本来 ...
- spark client + yarn计算
前提:完成hadoop + kerberos安全环境搭建. 安装配置spark client: 1. wget https://d3kbcqa49mib13.cloudfront.net/spark- ...
- 20145314郑凯杰《信息安全系统设计基础》第6周学习总结 part A
第4章 处理器体系结构 part 1 本部分对改章节的知识点进行总结: 一个处理器支持的指令和指令的字节级编码称为它的指令集体系结构(ISA). 不同的出路器有不同的ISA. ISA模型看上去应该是顺 ...
- Labview 查看一次while循环运行的时间
在while循环中增加一个移位寄存器,移位寄存器的初始值使用时间计数器,在while循环里面增加一个减法Vi,再增加一个时间计数器,两者做差,最后显示差值. 在这里只能显示大概运行时间.如下图.
- 1_jenkins环境搭建
前言 为什么要使用jenkins 可以实现批量部署.管理 支持常见的版本控制工具,git, svn等 发展成熟,使用范围广,容易找到解决方案 插件丰富,可以满足自己的需求 什么是jenkins 简单的 ...
- TortoiseSVN忽略文件夹
因为平时要做一些主干.分支的版本控制,发布增量补丁包工作,所以经常使用TortoiseSVN客户端.当然,eclipse中也安装了SVN插件,不过在打补丁方面感觉不如客户端.现在遇到了一个问题:同一项 ...
