Machine Learning系列--CRF条件随机场总结

根据《统计学习方法》一书中的描述，条件随机场（conditional random field, CRF）是给定一组输入随机变量条件下另一组输出随机变量的条件概率分布模型，其特点是假设输出随机变量构成马尔科夫随机场。

条件随机场是一种判别式模型。

一、理解条件随机场

1.1 HMM简单介绍

HMM即隐马尔可夫模型，它是处理序列问题的统计学模型，描述的过程为：由隐马尔科夫链随机生成不可观测的状态随机序列，然后各个状态分别生成一个观测，从而产生观测随机序列。

在这个过程中，不可观测的序列称为状态序列(state sequence), 由此产生的序列称为观测序列(observation sequence)。

该过程可通过下图描述：

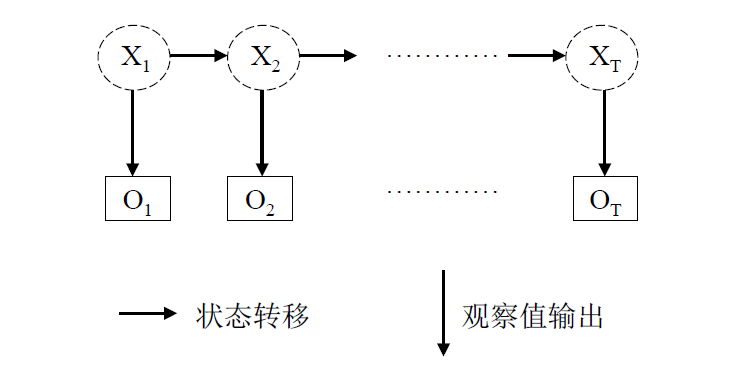
上图中， $X_1,X_2,…X_T$是隐含序列，而$O_1, O_2,..O_T$是观察序列。

隐马尔可夫模型由三个概率确定：

初始概率分布，即初始的隐含状态的概率分布，记为$\pi$；
状态转移概率分布，即隐含状态间的转移概率分布, 记为$A$；
观测概率分布，即由隐含状态生成观测状态的概率分布, 记为$B$。

以上的三个概率分布可以说就是隐马尔可夫模型的参数，而根据这三个概率，能够确定一个隐马尔可夫模型$\lambda = (A, B, \pi)$。

而隐马尔科夫链的三个基本问题为：

概率计算问题。即给定模型$\lambda = (A, B, \pi)$和观测序列$O$，计算在模型$\lambda$下观测序列出现的最大概率$P(O|\lambda)$，主要使用前向-后向算法解决；
学习问题。即给定观测序列$O$，估计模型的参数$\lambda$, 使得在该参数下观测序列出现的概率最大，即$P(O|\lambda)$最大，主要使用Baum-Welch算法EM迭代计算（若不涉及隐状态，则使用极大似然估计方法解决）；
解码问题。给定模型$\lambda = (A, B, \pi)$和观测序列$O$，计算最有可能产生这个观测序列的隐含序列$X$, 即使得概率$P(X|O, \lambda)$最大的隐含序列$X$，主要使用维特比算法（动态规划思想）解决。

HMM最初用于传染病模型和舆情传播问题，这些问题里面的当前状态可以简化为只与前一状态有关，即具备马尔科夫性质。但是，试想一个语言标注问题，模型不仅需要考虑前一状态的标注，也应该考虑后一状态的标注（例如我爱中国，名词+动词+名词，上下文信息更丰富）。由此，自然会对模型做出更多的假设条件，也就引出了图模型（当前状态与相连的状态都有关）+ 条件模型（当前的状态与隐状态有关）= 条件随机场。

1.2 概率无向图（马尔科夫随机场）

概率无向图模型又称马尔科夫随机场，是一个可以由无向图表示的联合概率分布。有向图是时间序列顺序的，又称贝叶斯网，HMM就属于其中的一种。HMM不能考虑序列的下一状态信息，这是有向图具有“方向性”所不能避免的。而无向图则可以将更多的相连状态考虑在当前状态内，考虑更全面的上下文信息。

概率图模型是由图表示的概率分布，记$G=(V, E)$是由结点集合$V$和边集合$E$组成的图。

首先我们需要明确成对马尔科夫性、局部马尔科夫性和全局马尔科夫性，这三种性质在理论上被证明是等价的。

成对马尔科夫性是指图$G$中任意两个没有边连接的结点所对应的的两个随机变量是条件独立的。

给定一个联合概率分布$P(Y)$，若该分布满足成对、局部或全局马尔科夫性，就称此联合概率分布为概率无向图模型或马尔科夫随机场。

局部马尔科夫性（黑色与白色点永远不相邻，即成对马尔科夫性）

1.3 条件随机场

条件随机场（CRF）是给定随机变量$X$的条件下，随机变量$Y$的马尔科夫随机场。在实际中，运用最多的是标注任务中的线性链条件随机场（linear chain conditional random field）。这时，在条件概率模型$P(Y|X)$中，$Y$是输出变量，表示标记序列，$X$是输入变量，表示需要标注的观测序列（状态序列）。

学习时，利用训练数据集通过极大似然估计或正则化的极大似然估计得到条件概率模型$\hat P(Y|X)$；

预测时，对于给定的输入序列$x$，求出条件概率$\hat P(y|x)$最大的输出序列$\hat y$。

一般性条件随机场定义如下：

设$X$与$Y$是随机变量，$P(Y|X)$是在给定$X$的条件下$Y$的条件概率分布。若随机变量$Y$构成一个由无向图$G=(V, E)$表示的马尔科夫随机场，即：

$$ P\left( {{Y_v}|X,{Y_w},w \ne v} \right) = P\left( {{Y_v}|X,{Y_w},w \sim v} \right). $$

对任意结点$v$成立，则称条件概率分布$\hat P(Y|X)$为条件随机场。式中$w \sim v$表示在图$G=(V, E)$中与结点$v$有边连接的所有结点$w$，$w \ne v$表示结点$v$以外的所有结点，$Y_v$与$Y_w$为结点$v$与$w$对应的随机变量。

类似地，线性链条件随机场有如下定义：

显然，线性链条件随机场是一般性条件随机场的一种特例。

设$ X=(X_1, X_2, ..., X_n) $，$Y=(Y_1, Y_2, ..., Y_n)$均为线性链表示的随机变量序列，若在给定随机变量序列$X$的条件下，随机变量序列$Y$的条件概率分布$P(Y|X)$构成条件随机场，即满足马尔科夫性：

$$ P\left( {{Y_i}|X,{Y_1}, \ldots ,{Y_{i - 1}},{Y_{i + 1}}, \ldots ,{Y_n}} \right) = P\left( {{Y_i}|X,{Y_{i - 1}},{Y_{i + 1}}} \right). $$

$$ i = 1,2, \ldots ,n (在i=1和n时只考虑单边). $$

则称$P(Y|X)$为线性链条件随机场。在标注问题中，$X$表示输入观测序列，$Y$表示对应的输出标记序列或状态序列。

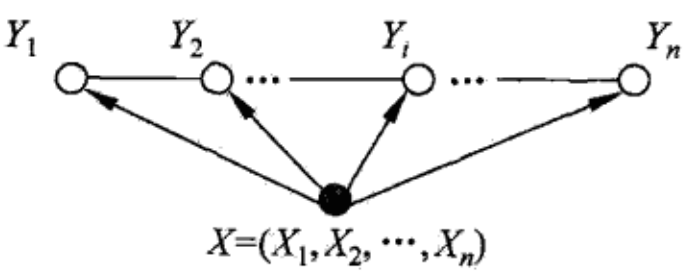
线性链条件随机场

$X$和$Y$具有相同图结构的线性链条件随机场

二、条件随机场的概率计算问题

条件随机场的概率计算问题是给定条件随机场$P(Y|X)$，输入序列$x$和输出序列$y$，计算条件概率$P(Y_i=y_i|x)$，$P(Y_{i-1}=y_{i-1}|x, Y_i=y_i|x)$以及相应的数学期望的问题。

条件随机场的概率计算和HMM的概率计算的思想没有本质区别，甚至可以说是完全一样的，区别只在于公式上稍作变化。

2.1 前向-后向算法

为了计算每个节点的概率，如书中提到的$P(Y = y_i | x)$的概率，对于这类概率计算，用前向或者后向算法其中的任何一个就可以解决。前向或后向算法，都是扫描一遍整体的边权值，计算图的$P(X)$，只是它们扫描的方向不同，一个从前往后，一个从后往前。所以书中的公式：
$$ P(x) = Z(x) = \sum_{y} P(y,x) = \alpha_n^T(x) \cdot 1 = 1^T\cdot \beta_1(x).$$
式中的$\alpha$为前向向量，$\beta$为后向向量。

按照前向-后向向量的定义，很容易计算标记序列在位置$i$是标记$y_i$的条件概率和在位置$i-1$与$i$是标记$y_{i-1}$和$y_i$的条件概率：
$$ P(Y_i = y_i | x) =\frac {\alpha_i^T(y_i | x) \beta_i(y_i | x)}{Z(x)}. $$
$$ P(Y_{i-1} = y_{i-1},Y_i = y_i | x) = \frac{\alpha_{i-1}^T(y_{i-1} | x)M_i(y_{i-1},y_i|x)\beta_i(y_i|x)}{Z(x)}. $$

2.2 计算期望

利用前向-后向向量，可以计算特征函数关于联合分布$P(X,Y)$和条件分布$P(Y|X)$的数学期望。

特征函数$f_k$关于条件分布$P(Y|X)$的数学期望是：

\begin{align*}
E_{P(Y|X)}[f_k] &= \sum_y P(y | x) f_k(y,x)\\
&=\sum_{i=1}^{n+1}\sum_{y_{i-1}y_i}f_k(y_{i-1},y_i,x,i)\frac{\alpha_{i-1}^T(y_{i-1} | x)M_i(y_{i-1},y_i|x)\beta_i(y_i|x)}{Z(x)}
& k = 1,2,\ldots, K.
\end{align*}

其中，有$Z(x) = \alpha_n^T(x) \cdot 1$.

假设经验分布为$\tilde P(X)$，特征函数$f_k$关于联合分布的数学期望是：

\begin{align*}
E_{p(X,Y)}[f_k] &= \sum_{x,y}P(X,Y)\sum_{i=1}^{n+1}f_k(y_{i-1},y_i,x,i) \\
&=\sum_{x} \hat P(x)\sum_{i=1}^{n+1}\sum_{y_{i-1}y_i}f_k(y_{i-1},y_i,x,i)\frac{\alpha_{i-1}^T(y_{i-1} | x)M_i(y_{i-1},y_i|x)\beta_i(y_i|x)}{Z(x)}
& k = 1,2,\ldots, K.
\end{align*}

其中，有$Z(x) = \alpha_n^T(x) \cdot 1$.

2.3 参数学习算法

条件随机场模型实际上是定义在时序数据上的对数线性模型，其学习方法包括极大似然估计和正则化的极大似然估计。具体的优化实现算法有改进的迭代尺度法IIS、梯度下降法以及拟牛顿法。

参数模型算法与最大熵模型算法的理论推导没有什么区别，仍是对训练的对数似然函数求极大值的过程。

训练数据的对数似然函数为：

$$ L(w) = L_{\hat p}(P_w) = \log \prod_{x,y}P_w(y | x)^{\hat P(x,y)}. $$

2.4 预测算法

维特比算法采用了经典的动态规划思想，该算法和HMM又是完全一致的，所以也不需要重新再推导一遍，可直接参看之前博文的【维特比算法】。那么，为什么需要使用维特比算法，而不是像最大熵模型那样，直接代入输入向量x即可？简单来说，是因为在整个图中，每个节点都是相互依赖，所以单纯的代入$P(Y | X)$是行不通的，你没法知道，到底哪个标签与哪个标签是可以联系在一块，所以必须把这个问题给【平铺】开来，即计算每一种可能的组合，但一旦平铺你会发现，如果穷举，那么运行时间是$O(k^T)$，$k$为标签数，$T$为对应的序列状态数。算法的开销相当大，而采用动态规划的一个好处在于，我们利用空间换时间，在某些中间节点直接记录最优值，以便前向扫描的过程中，直接使用，那么自然地运行时间就下去了。

三、条件随机场与其他模型的联系

3.1 经典对比图

经典对比图，来自论文：Sutton, Charles, and Andrew McCallum. "An introduction to conditional random fields." Machine Learning 4.4 (2011): 267-373.

从图中我们能找到CRF所处的位置，它可以从朴素贝叶斯方法用于分类经过sequence得到HMM模型，再由HMM模型conditional就得到了CRF。或者由朴素贝叶斯方法conditional成逻辑斯蒂回归模型，再sequence成CRF，两条路径均可。

首先来看看朴素贝叶斯的模型：
$$ P(Y | X ) = \frac{P(Y) P(X| Y)}{P(X)}. $$
其中特征向量$X$可以是$X= (x_1,x_2,...,x_n)$，由于朴素贝叶斯每个特征独立同分布，所以有:
$$ P(X|Y) = P(x_1 | Y) P(x_2 | Y)\cdots P(x_n|Y). $$
整理得：
$$ P(Y,X) = P(Y) \prod_{i=1}^nP(x_i | Y). $$

再来看一般形式的逻辑斯蒂回归模型：
\begin{align*}
P( Y | X) &= \frac {1}{Z(X)} exp(\theta_y + \sum_{i=1}^n \theta_{yi} f_i(X,Y))\\
&= \frac {1}{Z(X)} exp(\theta_y + \sum_{i=1}^n \theta_{yi} x_i).
\end{align*}
其中，$Z(X)$为规范化因子。

由朴素贝叶斯的模型继续推导：
\begin{align*}
P(Y, X) &= P(Y = y_c) \cdot \prod_{i = 1}^n P(X= x_i | Y = y_c) \\
&=exp[\log P(y_c)]exp[\sum_{i=1}^n \log P(x_i | y_c)]\\
&=exp\{\theta_y + \sum_{i=1}^n\theta_{yi} [X = x_i 且Y = y_c]\}.
\end{align*}

这就是从逻辑斯蒂回归模型看贝叶斯模型，我们能得到的结论。首先，逻辑斯蒂回归模型最终模型表达为条件概率，而非联合概率，因为它是判别式模型；其次，两者式中参数$\theta_{yi}$后的特征函数不同。贝叶斯模型考虑的是联合概率分布，所以它是生成式模型；而逻辑斯蒂回归模型，并不计算联合概率分布，而是把每个特征的实际值代入式中，计算条件判别概率。根据这样的思路，相信你能更好地理解上面的经典图。

3.2 HMM vs. MEMM vs. CRF

HMM -> MEMM： HMM模型中存在两个假设：一是输出观察值之间严格独立，二是状态的转移过程中当前状态只与前一状态有关。但实际上序列标注问题不仅和单个词相关，而且和观察序列的长度，单词的上下文，等等相关。MEMM解决了HMM输出独立性假设的问题。因为HMM只限定在了观测与状态之间的依赖，而MEMM引入自定义特征函数，不仅可以表达观测之间的依赖，还可表示当前观测与前后多个状态之间的复杂依赖。
MEMM -> CRF: CRF不仅解决了HMM输出独立性假设的问题，还解决了MEMM的标注偏置问题，MEMM容易陷入局部最优是因为只在局部做归一化，而CRF统计了全局概率，在做归一化时考虑了数据在全局的分布，而不是仅仅在局部归一化，这样就解决了MEMM中的标记偏置的问题。使得序列标注的解码变得最优解。
HMM、MEMM属于有向图，所以考虑了$x$与$y$的影响，但没将$x$当做整体考虑进去。CRF属于无向图，没有这种依赖性，克服此问题。

参考内容：

1. 如何用简单易懂的例子解释条件随机场（CRF）模型？它和HMM有什么区别？https://www.zhihu.com/question/35866596

2. 条件随机场学习笔记：https://blog.csdn.net/u014688145/article/details/58055750

3. 《统计学习方法》，李航