POJ 3384 Feng Shui （半平面交）

Feng Shui

Time Limit: 2000MS		Memory Limit: 65536K
Total Submissions: 3743		Accepted: 1150		Special Judge

Description

Feng shui is the ancient Chinese practice of placement and arrangement of space to achieve harmony with the environment. George has recently got interested in it, and now wants to apply it to his home and bring harmony to it.

There is a practice which says that bare floor is bad for living area since spiritual energy drains through it, so George purchased two similar round-shaped carpets (feng shui says that straight lines and sharp corners must be avoided). Unfortunately, he is unable to cover the floor entirely since the room has shape of a convex polygon. But he still wants to minimize the uncovered area by selecting the best placing for his carpets, and asks you to help.

You need to place two carpets in the room so that the total area covered by both carpets is maximal possible. The carpets may overlap, but they may not be cut or folded (including cutting or folding along the floor border) — feng shui tells to avoid straight lines.

Input

The first line of the input file contains two integer numbers n and r — the number of corners in George’s room (3 ≤ n ≤ 100) and the radius of the carpets (1 ≤ r ≤ 1000, both carpets have the same radius). The following n lines contain two integers x_i and y_i each — coordinates of the i-th corner (−1000 ≤ x_i, y_i ≤ 1000). Coordinates of all corners are different, and adjacent walls of the room are not collinear. The corners are listed in clockwise order.

Output

Write four numbers x₁, y₁, x₂, y₂ to the output file, where (x₁, y₁) and (x₂, y₂) denote the spots where carpet centers should be placed. Coordinates must be precise up to 4 digits after the decimal point.

If there are multiple optimal placements available, return any of them. The input data guarantees that at least one solution exists.

Sample Input

#1	5 2 -2 0 -5 3 0 8 7 3 5 0
#2	4 3 0 0 0 8 10 8 10 0

Sample Output

#1	-2 3 3 2.5
#2	3 5 7 3

Hint

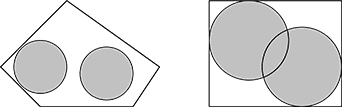
Source

Northeastern Europe 2006, Northern Subregion

给你两个圆，半径相等，求放在一个凸多边形里两个圆不碰到边界的圆心。两个圆是可以重叠的。

半平面交，向内推进R，然后求组成多边形的最远的两个点即可。

 /* ***********************************************
 Author        :kuangbin
 Created Time  :2013/8/18 15:52:28
 File Name     :F:\2013ACM练习\专题学习\计算几何\半平面交\POJ3384.cpp
 ************************************************ */

 #include <stdio.h>
 #include <string.h>
 #include <iostream>
 #include <algorithm>
 #include <vector>
 #include <queue>
 #include <set>
 #include <map>
 #include <string>
 #include <math.h>
 #include <stdlib.h>
 #include <time.h>
 using namespace std;
 const double eps = 1e-;
 const double PI = acos(-1.0);
 int sgn(double x)
 {
     if(fabs(x) < eps) return ;
     if(x < ) return -;
     else return ;
 }
 struct Point
 {
     double x,y;
     Point(){}
     Point(double _x,double _y)
     {
         x = _x; y = _y;
     }
     Point operator -(const Point &b)const
     {
         return Point(x - b.x, y - b.y);
     }
     double operator ^(const Point &b)const
     {
         return x*b.y - y*b.x;
     }
     double operator *(const Point &b)const
     {
         return x*b.x + y*b.y;
     }
 };
 struct Line
 {
     Point s,e;
     double k;
     Line(){}
     Line(Point _s,Point _e)
     {
         s = _s; e = _e;
         k = atan2(e.y - s.y,e.x - s.x);
     }
     Point operator &(const Line &b)const
     {
         Point res = s;
         double t = ((s - b.s)^(b.s - b.e))/((s - e)^(b.s - b.e));
         res.x += (e.x - s.x)*t;
         res.y += (e.y - s.y)*t;
         return res;
     }
 };
 //半平面交，直线的左边代表有效区域
 bool HPIcmp(Line a,Line b)
 {
     if(fabs(a.k - b.k) > eps)return a.k < b.k;
     return ((a.s - b.s)^(b.e - b.s)) < ;
 }
 Line Q[];
 void HPI(Line line[], int n, Point res[], int &resn)
 {
     int tot = n;
     sort(line,line+n,HPIcmp);
     tot = ;
     for(int i = ;i < n;i++)
         if(fabs(line[i].k - line[i-].k) > eps)
             line[tot++] = line[i];
     int head = , tail = ;
     Q[] = line[];
     Q[] = line[];
     resn = ;
     for(int i = ; i < tot; i++)
     {
         if(fabs((Q[tail].e-Q[tail].s)^(Q[tail-].e-Q[tail-].s)) < eps || fabs((Q[head].e-Q[head].s)^(Q[head+].e-Q[head+].s)) < eps)
             return;
         while(head < tail && (((Q[tail]&Q[tail-]) - line[i].s)^(line[i].e-line[i].s)) > eps)
             tail--;
         while(head < tail && (((Q[head]&Q[head+]) - line[i].s)^(line[i].e-line[i].s)) > eps)
             head++;
         Q[++tail] = line[i];
     }
     while(head < tail && (((Q[tail]&Q[tail-]) - Q[head].s)^(Q[head].e-Q[head].s)) > eps)
         tail--;
     while(head < tail && (((Q[head]&Q[head-]) - Q[tail].s)^(Q[tail].e-Q[tail].e)) > eps)
         head++;
     if(tail <= head + )return;
     for(int i = head; i < tail; i++)
         res[resn++] = Q[i]&Q[i+];
     if(head < tail - )
         res[resn++] = Q[head]&Q[tail];
 }
 Point p[];
 Line line[];
 //*两点间距离
 double dist(Point a,Point b)
 {
     return sqrt((a-b)*(a-b));
 }
 void change(Point a,Point b,Point &c,Point &d,double p)//将线段ab往左移动距离p
 {
     double len = dist(a,b);
     double dx = (a.y - b.y)*p/len;
     double dy = (b.x - a.x)*p/len;
     c.x = a.x + dx; c.y = a.y + dy;
     d.x = b.x + dx; d.y = b.y + dy;
 }
 int main()
 {
     //freopen("in.txt","r",stdin);
     //freopen("out.txt","w",stdout);
     int n;
     double r;
     while(scanf("%d%lf",&n,&r) == )
     {
         for(int i = ;i < n;i++)
             scanf("%lf%lf",&p[i].x,&p[i].y);
         reverse(p,p+n);
         for(int i = ;i < n;i++)
         {
             Point t1,t2;
             change(p[i],p[(i+)%n],t1,t2,r);
             line[i] = Line(t1,t2);
         }
         int resn;
         HPI(line,n,p,resn);
         int res1 = , res2 = ;
         for(int i = ;i < resn;i++)
             for(int j = i;j < resn;j++)
                 if(dist(p[i],p[j]) > dist(p[res1],p[res2]))
                     res1 = i, res2 = j;
         printf("%.5f %.5f %.5f %.5f\n",p[res1].x,p[res1].y,p[res2].x,p[res2].y);
     }
     return ;
 }