PID控制原理和算法

闭环控制是根据控制对象输出反馈来进行校正的控制方式，它是在测量出实际与计划发生偏差时，按定额或标准来进行纠正的。比如控制一个电机的转速，就得有一个测量转速的传感器，并将结果反馈到控制路线上。提到闭环控制算法，不得不提PID，它是闭环控制算法中最简单的一种。PID是比例 (Proportion) 积分 ,(Integral) 微分 ,(Differential coefficient) 的缩写，分别代表了三种控制算法。通过这三个算法的组合可有效地纠正被控制对象的偏差，从而使其达到一个稳定的状态。如下图所示为PID的流程。

其中r(t)表示给定输入值，c(t)表示实际输出值，e(t)表示信号偏差量，u(t)表示修正量。

1、比例(P)、积分(I)、微分(D)控制算法各有作用

1）、比例，反应系统的基本（当前）偏差e(t)，系数大，可以加快调节，减小误差，但过大的比例使系统稳定性下降，甚至造成系统不稳定；比例控制的比例系数如果太小，即调节后的电位器转角与位置L的差值太小，调节的力度不够，使系统输出量变化缓慢，调节所需的总时间过长。比例系数如果过大，即调节后电位器转角与位置L的差值过大，调节力度太强，将造成调节过头，甚至使温度忽高忽低，来回震荡。增大比例系数使系统反应灵敏，调节速度加快，并且可以减小稳态误差。但是比例系数过大会使超调量增大，振荡次数增加，调节时间加长，动态性能变坏，比例系数太大甚至会使闭环系统不稳定。 单纯的比例控制很难保证调节得恰到好处，完全消除误差。如下图所示：

2）、积分，反应系统的累计偏差，使系统消除稳态误差，提高无差度，因为有误差，积分调节就进行，直至无误差；积分调节的“大方向”是正确的，积分项有减小误差的作用。一直要到系统处于稳定状态，这时误差恒为零，比例部分和微分部分均为零，积分部分才不再变化，并且刚好等于稳态时需要的控制器的输出值，对应于上述温度控制系统中电位器转角的位置L。因此积分部分的作用是消除稳态误差，提高控制精度，积分作用一般是必须的。 如下图所示：

3）、微分，反映系统偏差信号的变化率e(t)-e(t-1)，具有预见性，能预见偏差变化的趋势，产生超前的控制作用，在偏差还没有形成之前，已被微分调节作用消除，因此可以改善系统的动态性能。但是分对噪声干扰有放大作用，加强微分对系统抗干扰不利。误差的微分就是误差的变化速率，误差变化越快，其微分绝对值越大。误差增大时，其微分为正；误差减小时，其微分为负。控制器输出量的微分部分与误差的微分成正比，反映了被控量变化的趋势。如下图所示：

　　闭环控制系统的振荡甚至不稳定的根本原因在于有较大的滞后因素。因为微分项能预测误差变化的趋势，这种“超前”的作用可以抵消滞后因素的影响。适当的微分控制作用可以使超调量减小，增加系统的稳定性。

　　对于有较大的滞后特性的被控对象，如果PI控制的效果不理想，可以考虑增加微分控制，以改善系统在调节过程中的动态特性。如果将微分时间设置为0，微分部分将不起作用。

　　微分时间与微分作用的强弱成正比，微分时间越大，微分作用越强。如果微分时间太大，在误差快速变化时，响应曲线上可能会出现“毛刺”。

　　微分控制的缺点是对干扰噪声敏感，使系统抑制干扰的能力降低。为此可在微分部分增加惯性滤波环节。

　　一种PID控制算法的流程图，如下所示：

2、PID参数调节

　　在整定PID控制器参数时，可以根据控制器的参数与系统动态性能和稳态性能之间的定性关系，用实验的方法来调节控制器的参数。有经验的调试人员一般可以较快地得到较为满意的调试结果。在调试中最重要的问题是在系统性能不能令人满意时，知道应该调节哪一个参数，该参数应该增大还是减小。

　　为了减少需要整定的参数，首先可以采用PI控制器。为了保证系统的安全，在调试开始时应设置比较保守的参数，例如比例系数不要太大，积分时间不要太小，以避免出现系统不稳定或超调量过大的异常情况。给出一个阶跃给定信号，根据被控量的输出波形可以获得系统性能的信息，例如超调量和调节时间。应根据PID参数与系统性能的关系，反复调节PID的参数。

　　如果阶跃响应的超调量太大，经过多次振荡才能稳定或者根本不稳定，应减小比例系数、增大积分时间。如果阶跃响应没有超调量，但是被控量上升过于缓慢，过渡过程时间太长，应按相反的方向调整参数。

　　如果消除误差的速度较慢，可以适当减小积分时间，增强积分作用。

　　反复调节比例系数和积分时间，如果超调量仍然较大，可以加入微分控制，微分时间从0逐渐增大，反复调节控制器的比例、积分和微分部分的参数。

　　总之，PID参数的调试是一个综合的、各参数互相影响的过程，实际调试过程中的多次尝试是非常重要的，也是必须的。

常用的控制方式：P,PI,PD,PID控制算法

注：以上原理部分内容参考自以下资料：

[1]. PID控制最通俗的解释与PID参数的整定方法

[2]. PID控制算法

3、代码实现

　　以对常数和函数控制为例，Maltab实现演示，代码如下：

 clear all;
 close all;
 ts=0.001;
 sys=tf(,[0.125,, ]);
 dsys=c2d(sys,ts,'z');
 [num,den]=tfdata(dsys,'v');
 u_1=0.0;u_2=0.0;
 y_1=0.0;y_2=0.0;
 x=[,,]';
 error_1=;
 error_2=;
 for k=::
     time(k)=k*ts;
     S=;
     if S==
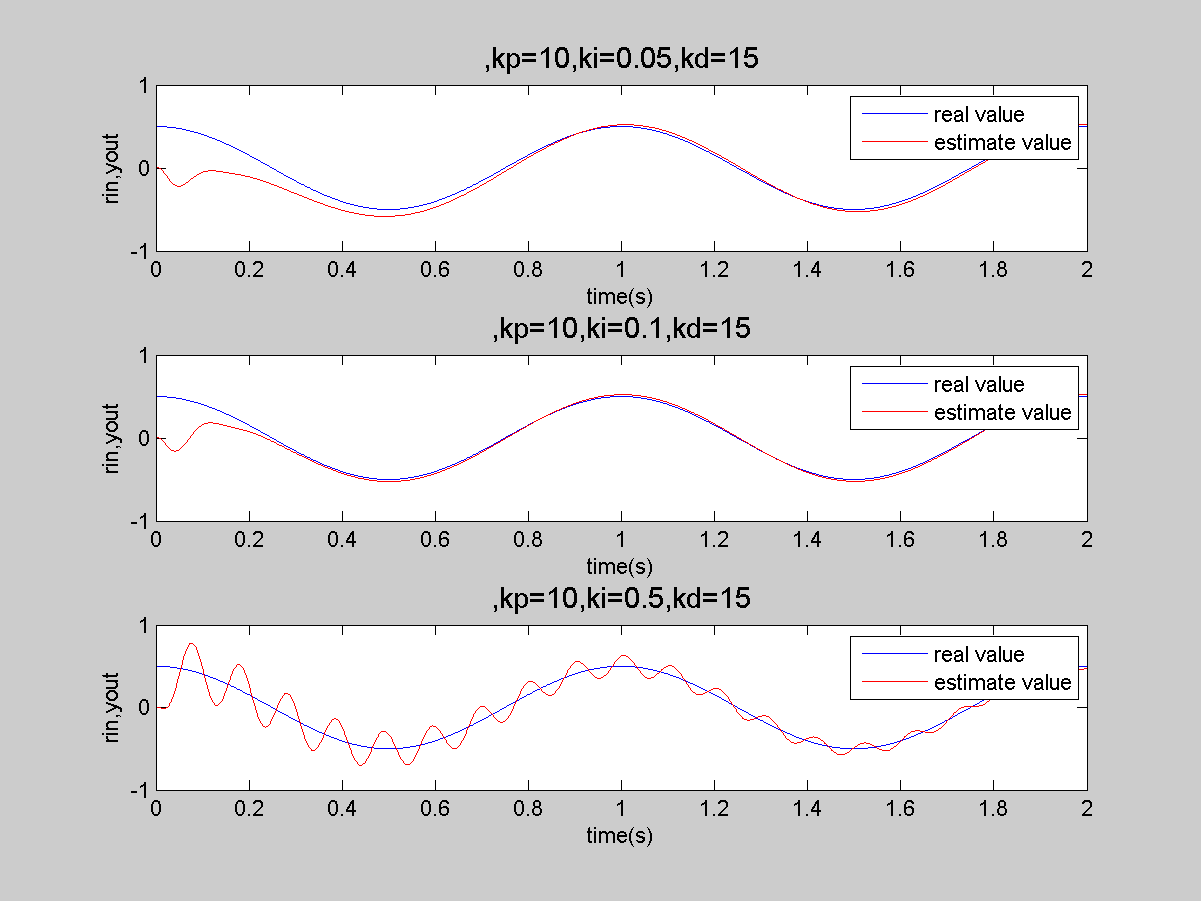
         kp=;ki=0.1;kd=;
         rin(k)=;                       %Step Signal
     elseif S==
         %kp=;ki=0.0;kd=;          %Sine Signal
          kp=;ki=0.1;kd=;          %Sine Signal
         rin(k)=0.5*cos(*pi*k*ts);
     end
     du(k)=kp*x()+kd*x()+ki*x();    %PID Controller
     u(k)=u_1+du(k);
     %Restricting the output of controller
     if u(k)>=
         u(k)=;
     end
     if u(k)<=-
         u(k)=-;
     end
     %Linear model
     yout(k)=-den()*y_1-den()*y_2+num()*u_1+num()*u_2;
     error(k)=rin(k)-yout(k);
     %Return of parameters
     u_2=u_1;u_1=u(k);
     y_2=y_1;y_1=yout(k);
     x()=error(k)-error_1;          %Calculating P
     x()=error(k)-*error_1+error_2;   %Calculating D
     x()=error(k);      %Calculating I
     error_2=error_1;
     error_1=error(k);
 end
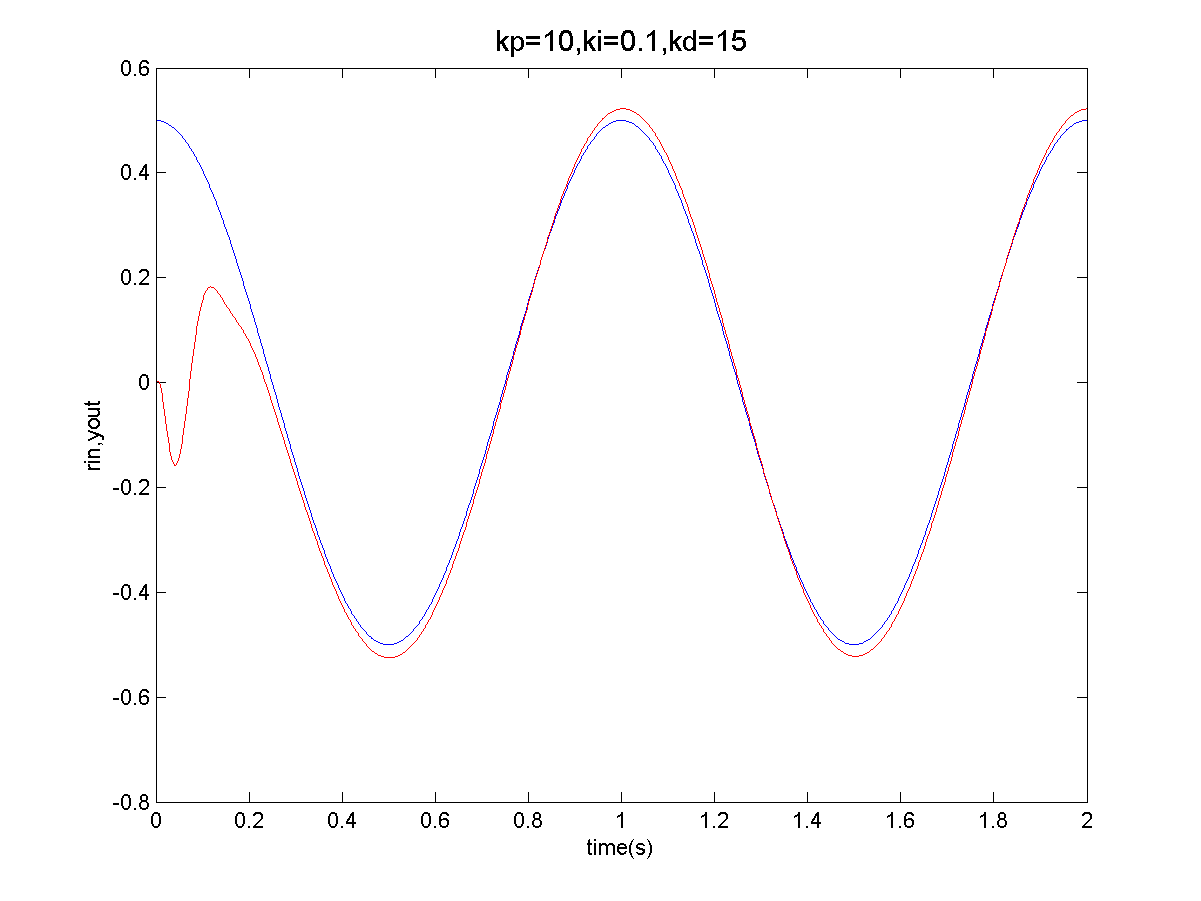
 figure();
 plot(time,rin,'b',time,yout,'r');
 xlabel('time(s)'),ylabel('rin,yout');
 title(['kp=10,ki=0.1,kd=15'],'FontSize',,'Color','k');
 saveas(,'pid','png');
 figure();
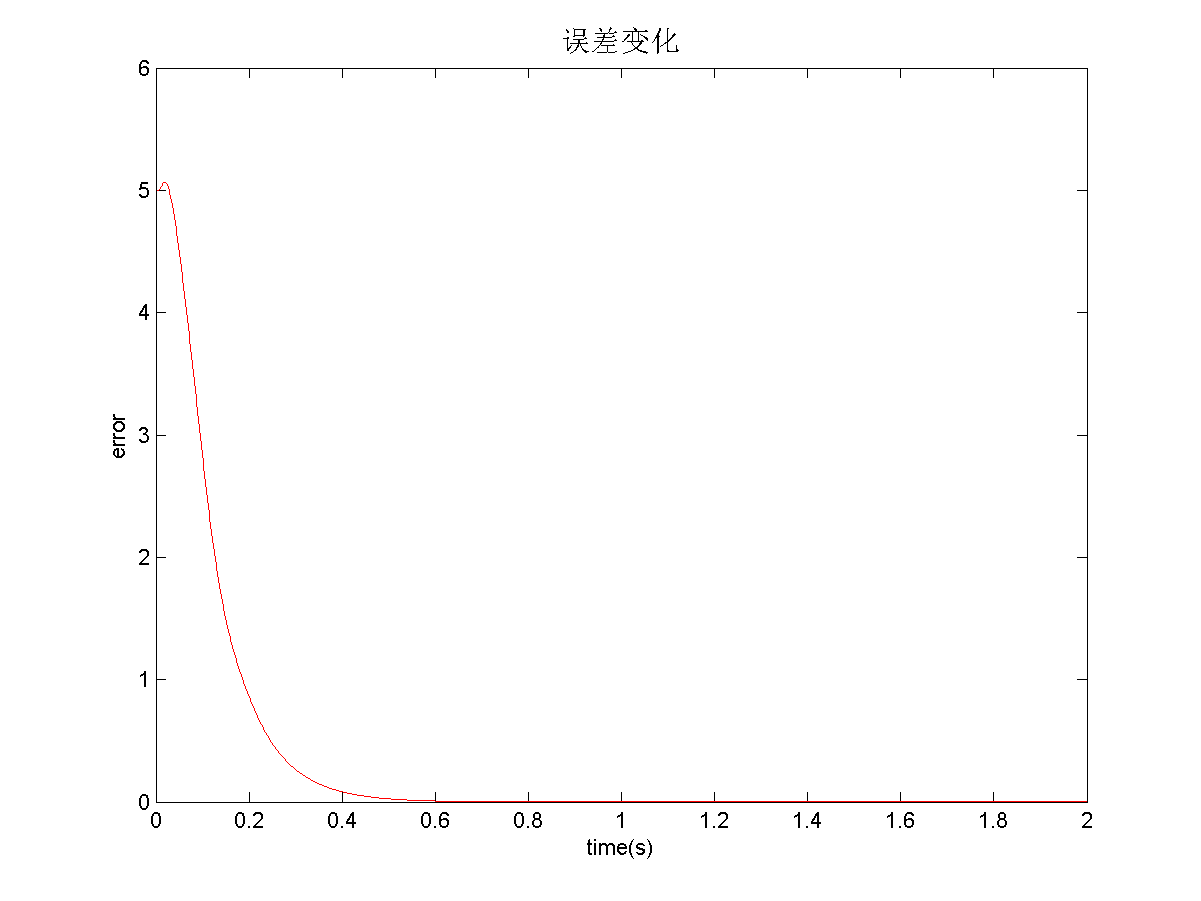
 plot(time,error,'r')
 title(['误差变化'],'FontSize',,'Color','k');
 xlabel('time(s)');ylabel('error');
 saveas(,'pid_err','png');

效果图

　　1)、常数y = 5纠正：

　　2)、曲线y = 0.5*cos(t)纠正：

代码工程下载：PID算法实现