ref:Spring Integration Zip 不安全解压（CVE-2018-1261）漏洞分析

ref:https://mp.weixin.qq.com/s/SJPXdZWNKypvWmL-roIE0Q

0x00 漏洞概览

漏洞名称：Spring Integration Zip不安全解压

漏洞编号：CVE-2018-1261

漏洞级别：严重（官方定级，比高危还高）

漏洞危害：在spring-integration-zip.v1.0.1.RELEASE之前的版本中，恶意用户通过在压缩文件中构造包含有特定文件名称的文件（受影响文件格式有bzip2, tar, xz, war, cpio, 7z），应用程序使用spring-integration-zip进行解压时，会导致跨目录任意写入文件漏洞的攻击。进而有可能被Getshell，远程控制。

漏洞加固：更新升级，zip.v1.0.2.RELEASE版本

漏洞利用前置条件：

使用了spring-integration-zip库

接收并解压了来自不可信来源的压缩文件

0x01 漏洞分析

补丁比对

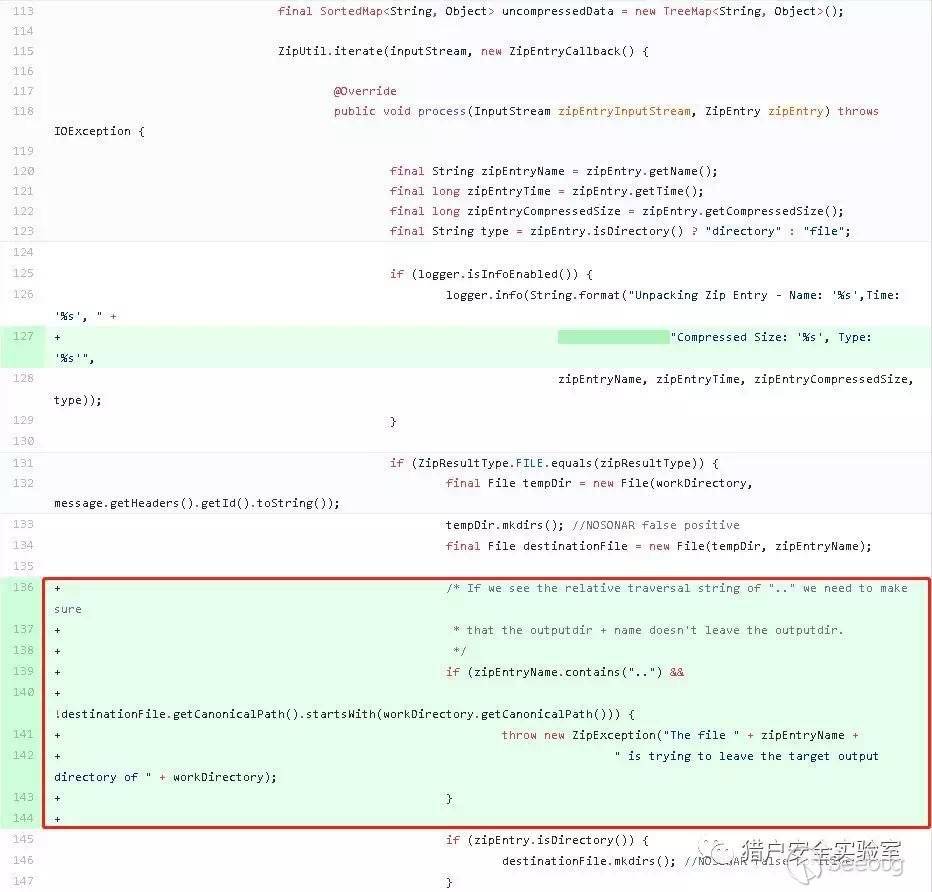
zip.v1.0.1.RELEASE在UnZipTransformer调用ZipUtil.iterate()时定义的回调中增加了一段对文件名称校验的代码片段（在5月11日凌晨更新的zip.v1.0.2.RELEASE版本中，对Byte[]类型的分支逻辑也增加了文件名称校验，并且删除了对名称中..的判断，直接校验名称是否以工作区目录开头）。

通过上述内容我们大致可以猜测这个漏洞的原理：攻击者可以通过构造一个包含名称带../前缀的文件的压缩包，使spring-integration-zip进行解压时该文件跳出解压目录被创建。

而且在zip.v1.0.1.RELEASE也增加了对这类压缩包的测试用例，并且十分贴心的附上了一个“恶意”的压缩包测试文件zip-malicious-traversal.zip。

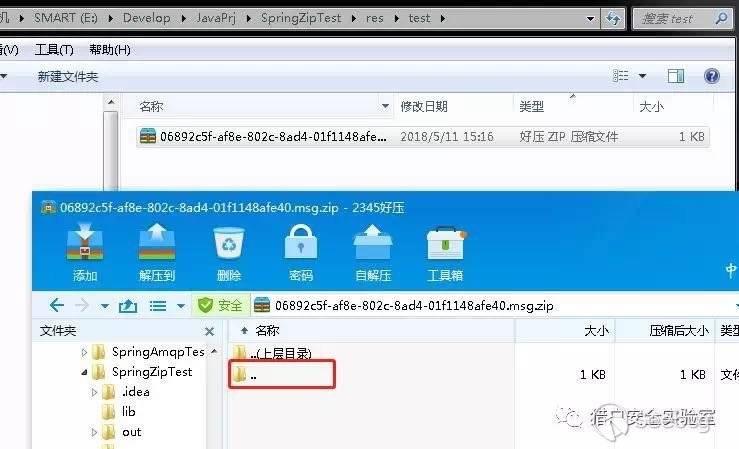
我们先看看这个压缩包长什么样子：

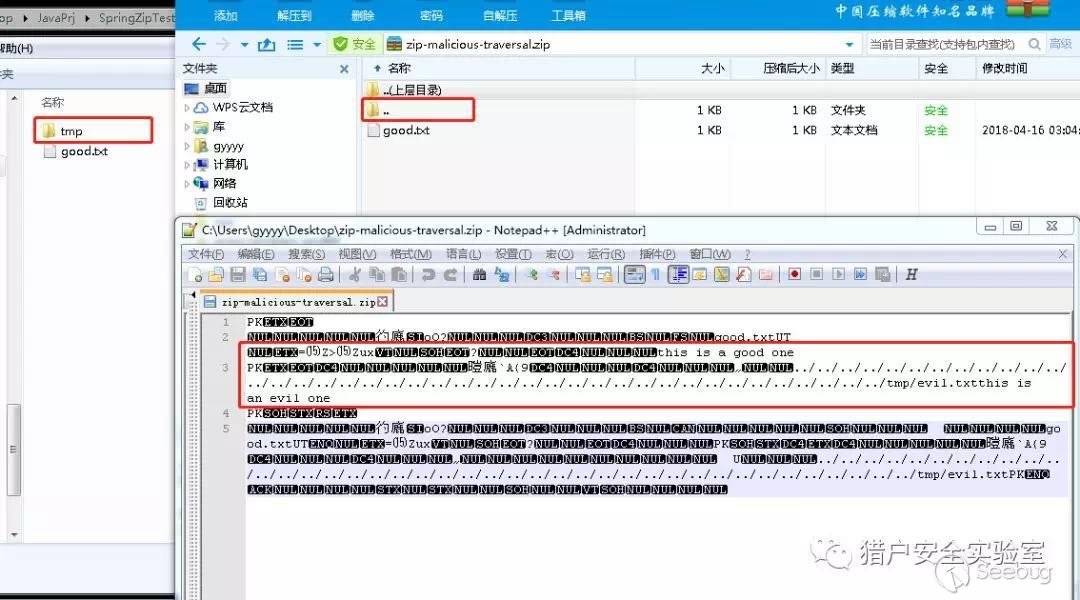
稍微说明一下：

右上，压缩包正常打开的目录结构

右下，压缩包的文本形式数据

左，压缩包解压后的目录结构

从文本数据中不难看出，这个压缩包中存在一个以很多../开头为名称的文件evil.txt。以压缩工具打开查看时，它以目录树形式显示，而解压后最深层的有效目录及文件被提取至根目录（说明使用的这个工具不存在这类解压漏洞）。

这样就可以很清楚的知道，这个压缩包如果被zip.v1.0.0.RELEASE解压，evil.txt文件将会被写入工作区目录对应盘符下的tmp目录中。

搭个调试环境跑起来看看。

0x02 环境搭建

IDE：IDEA

JDK：1.7

Libraries

spring-integration-zip.1.0.0.RELEASE

spring-integration-core.4.3.10.RELEASE

spring-integration-file.4.3.10.RELEASE

zt-zip.1.11

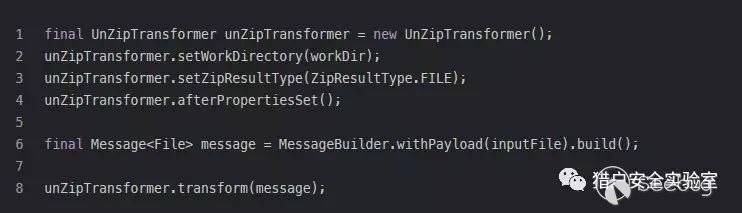
关键代码如下（参考官方测试用例即可）：

流程跟踪

流程很简单，示例中的UnZipTransformer.transform()会调用doZipTransform()解压，在遍历压缩包内目录及文件时，回调ZipEntryCallback.process()对其进行处理。

当遍历到evil.txt时，它被识别为一个文件，而并不是多层的目录结构，那一堆乱七八糟的只是它的文件名：

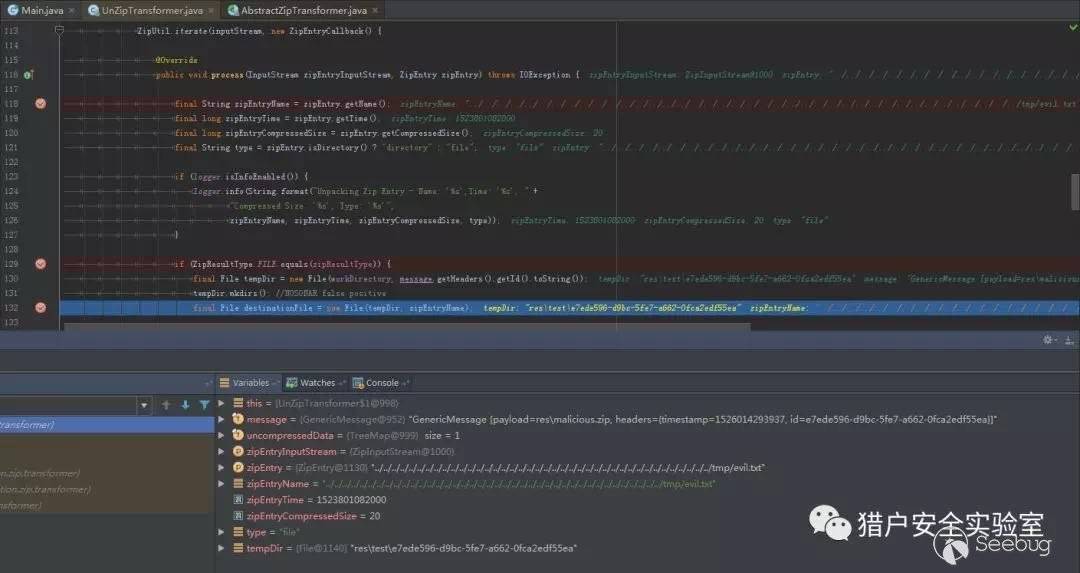
而对正常压缩包遍历到目录时应该是这样的：

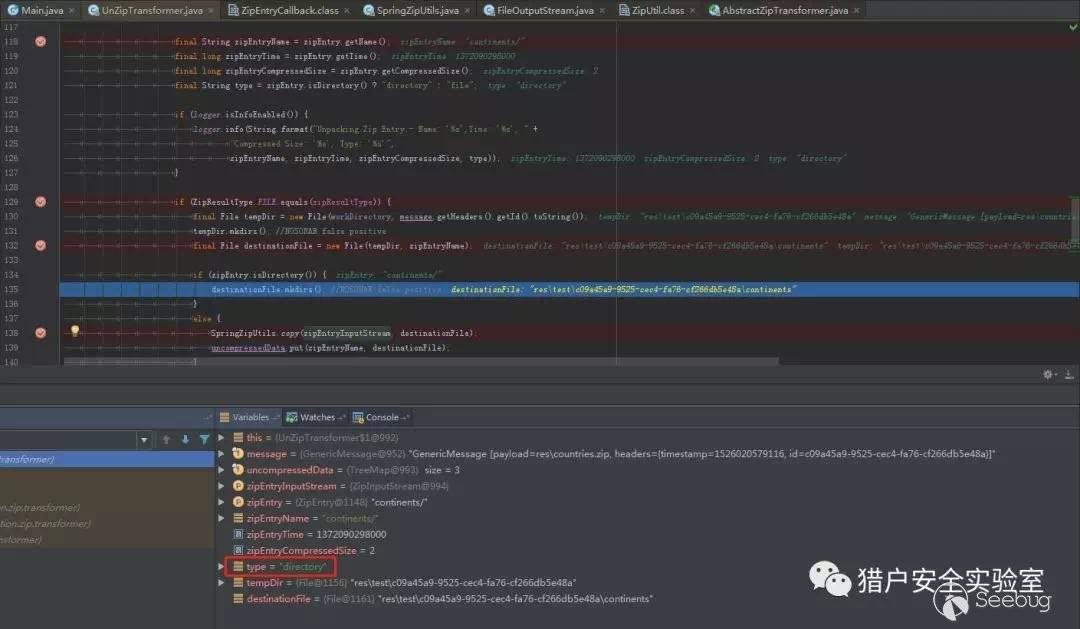
然后根据文件名在工作区目录中创建对应文件（子目录会在遍历时被提前创建），并调用org.apache.commons.io包中的IOUtils.copy()复制文件数据。

此时，解压的文件名被转换为绝对路径：

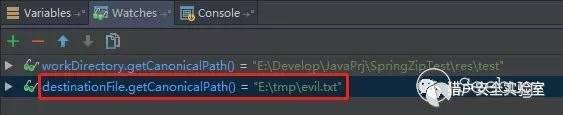
程序运行结束，查看E:\tmp\目录下发现evil.txt文件（由于Win操作系统默认没有/tmp目录，因此我在测试前提前创建了一个，也可以直接使用已存在目录，如Web Root:P）：

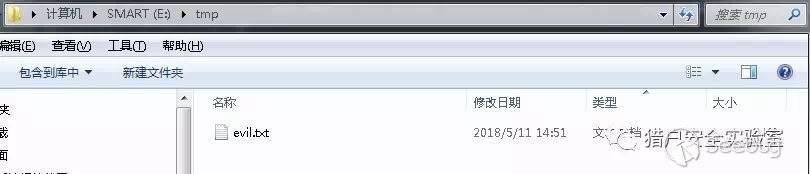
0x03 POC生成

知道了漏洞原理后，我们比较好奇的是如何生成这种特殊的压缩文件，已知方法有（如果有更方便的方法，请告诉我）：

用二进制数据构造符合压缩包数据结构的文件

使用spring-integration-zip压缩

我们用方法2做个测试，关键代码如下：

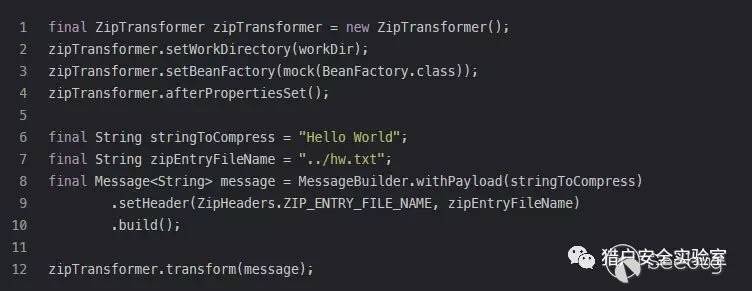
再解压试试

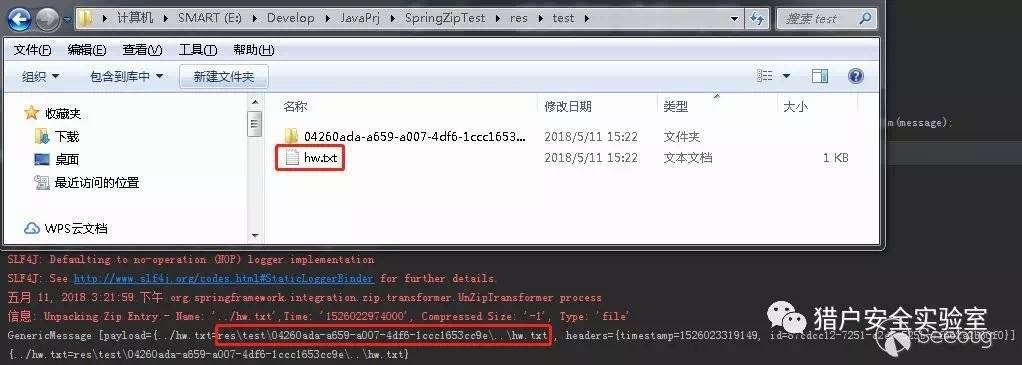
可以看到hw.txt跳出解压目录外层来了，OK，打完收工。

参考