【[AHOI2008]逆序对】

被锤爆了

被这个题搞得自闭了一上午，觉得自己没什么前途了

我又没有看出来这个题的一个非常重要的性质

我们填进去的数一定是单调不降的

首先如果填进去的数并不是单调不降的，那么填进去本身就会产生一些逆序对，感性理解好像是单调不降更优，这里还是严谨证明一下吧

考虑一下树状数组求逆序对的过程，显然就是求出每一个数前面有多少个比它大的数

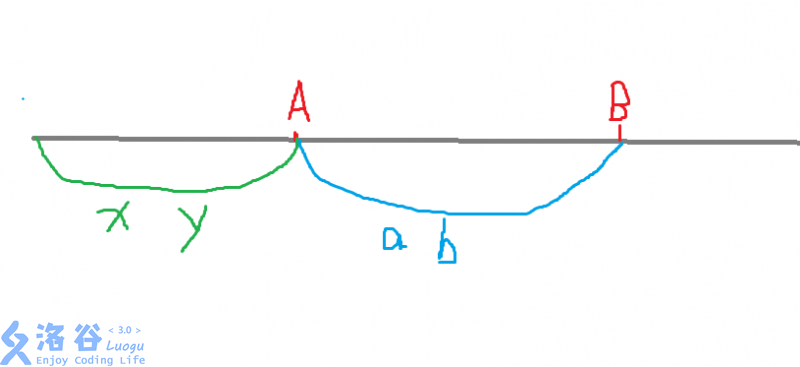
这张图好丑啊

设\(A<B\)，\(x\)表示那段绿色区间里大于\(A\)的数，\(y\)表示绿色区间里大于\(B\)的数，\(a\)表示蓝色区间里大于\(A\)的数，\(b\)表示蓝色区间里大于\(B\)的数

这个时候我们如果用树状数组来统计一下答案的话，\(A,B\)的贡献就是\(x+y+b\)

如果交换一下\(A\)和\(B\)的位置，那么这个时候答案就会变成\(x+a+y+1\)

非常显然的是\(b<=a\)，所以可以得出\(x+y+b<x+a+y+1\)，所以不交换更优

之后有了这个性质，我们就可以做一个\(dp\)了，设\(dp[i][j]\)表示填到了\(i\)位置，最靠后的一个\(-1\)位置填了\(j\)这个时候的最小逆序对是多少

就可以一边树状数组一边\(dp\)了

复杂度\(O(nklogk)\)

代码

#include<iostream>
#include<cstring>
#include<cstdio>
#define LL long long
#define lowbit(x) ((x)&(-x))
#define re register
#define maxn 100005
#define min(a,b) ((a)<(b)?(a):(b))
inline int read()
{
	char c=getchar();
	int x=0,r=1;
	while(c<'0'||c>'9')
	{
		if(c=='-') r=-1;
		c=getchar();
	}
	while(c>='0'&&c<='9')
		x=(x<<3)+(x<<1)+c-48,c=getchar();
	return x*r;
}
LL c[105];
int n,m;
LL ans;
LL dp[maxn][101];
LL mx[101];
int pre[maxn];
int a[maxn];
int beh[maxn][101];
inline void add(int x)
{
	for(re int i=x;i<=m;i+=lowbit(i)) c[i]++;
}
inline LL ask(int x)
{
	LL now=0;
	for(re int i=x;i;i-=lowbit(i)) now+=c[i];
	return now;
}
int main()
{
	int cnt=0;
	n=read(),m=read();
	for(re int i=1;i<=n;i++)
	{
		a[i]=read();
		if(a[i]==-1&&!cnt) cnt=i;
		pre[i]=pre[i-1]+(a[i]==-1);
	}
	if(!cnt) cnt=n+1;
	for(re int i=1;i<cnt;i++)
	{
		ans+=ask(m)-ask(a[i]);
		add(a[i]);
	}
	if(cnt==n+1)
	{
		std::cout<<ans;
		return 0;
	}
	for(re int i=n;i;i--)
	{
		for(re int j=1;j<=m;j++)
			beh[i][j]=beh[i+1][j];
		if(a[i]==-1) continue;
		for(re int j=a[i];j<=m;j++) beh[i][j]++;
	}
	memset(dp,20,sizeof(dp));
	for(re int i=1;i<=m;i++)
		dp[cnt][i]=ans+ask(m)-ask(i)+beh[cnt][i-1];
	memset(mx,20,sizeof(mx));
	for(re int j=1;j<=m;j++)
		mx[j]=min(mx[j-1],dp[cnt][j]);
	for(re int i=cnt+1;i<=n;i++)
	{
		if(a[i]!=-1)
		{
			LL now=ask(m)-ask(a[i]);
			for(re int j=1;j<=m;j++)
				dp[i][j]=now+dp[i-1][j];
			add(a[i]);
		}
		else
		{
			for(re int j=1;j<=m;j++)
			{
				LL now=ask(m)-ask(j);
				dp[i][j]=mx[j]+now+beh[i][j-1];
			}
		}
		memset(mx,20,sizeof(mx));
		for(re int j=1;j<=m;j++)
			mx[j]=min(mx[j-1],dp[i][j]);
	}
	LL Ans=0x7ffffffff;
	for(re int i=1;i<=m;i++)
		Ans=min(Ans,dp[n][i]);
	std::cout<<Ans;
	return 0;
}