hdu1452 Happy 2004(规律+因子和+积性函数)

Happy 2004

题意:s为2004^x的因子和，求s%29.     （题于文末）

知识点：

素因子分解：n = p1 ^ e1 * p2 ^ e2 *..........*pn ^ en

因子和：    Sum=(p1^0+p1^1….p1^e1)*(p2^0+p2^1…p2^e2)……(pn^0+…pn^en)

=;

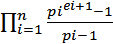积性函数：s(xy)=s(x)*s(y)    (比如：幂函数，因子和，欧拉函数，莫比乌斯函数）

对于正整数n的一个算术函数 f(n)，若f(1)=1，且当a,b互质时f(ab)=f(a)f(b)，在数论上就称它为积性函数。

若对于某积性函数 f(n)，就算a, b不互质，也有f(ab)=f(a)f(b)，则称它为完全积性的。

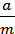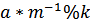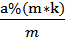
%运算：  % k = =   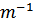                 为m模k的逆元

题解：

一般模值(mod)较小时会有规律，可以找下循环节。

发现答案的循环结为28.

#include<iostream>
using namespace std;
int a[]={6,16,8,10,25,7,14,3,23,17,13,17,0,27,7,14,15,17,26,26,20,17,9,22,22,23,0,1};

int main()
{
    int x;
    while(cin>>x&&x)
    {
        cout<<a[(x-1)%28]<<endl;
    }
    /*找规律过程

    for(x=1;x<=100;x++)
    {
        int a2=1,a3=1,a167=1,ans2=0,ans3=0,ans167=0;
        for(int i=0;i<=x*2;i++)
        {
            ans2+=a2;
            a2*=2;
            ans2%=29;
            a2%=29;
        }
        for(int i=0;i<=x;i++)
        {
            ans3+=a3;
            a3*=3;
            ans3%=29;
            a3%=29;
        }
        for(int i=0;i<=x;i++)
        {
            ans167+=a167;
            a167*=167;
            ans167%=29;
            a167%=29;
        }
        cout<<ans2*ans3*ans167%29<<endl;
    }*/
    return 0;
}

再给出一般解：

因子和为积性函数，so  sum(2004^X)= sum(2^2X) * sum(3^X)* sum(167^X)

sum(2004^X)%29=sum(2^2X) %29  *  sum(3^X)%29  *  sum(167^X)%29

=sum((2%29)^2X) %29  *  sum((3%29)^X)%29  *  sum((167%29)^X)%29

=sum(2^2X)   *  sum(3^X)  *  sum(22^X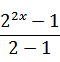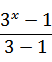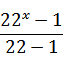)%29

=   *      *   %29

2的逆元是15  ，21的逆元是18

=（（2^(2X+1)-1）* (3^(X+1)-1)*15 *(22^(X+1)-1)*18）%29

快速幂取模，实现2^2x,3^x,22^x   O(logn)的运算

#include <iostream>
#include <cstdio>
#include <cmath>    

using namespace std;    

int quick_mod( int a, int n )
{
    int b = 1;
    while( n > 1 )
        if( n % 2 == 0 )
        {
            a = ( a * a ) % 29;
            n /= 2;
        }
        else
        {
            b = b * a % 29;
            n--;
        }
        return a * b % 29;
}
int main()
{
    int X;
    int a, b, c;
    while( scanf("%d",&X), X )
    {
        a = quick_mod( 2, 2 * X + 1 );
        b = quick_mod( 3, ( X + 1 ) );
        c = quick_mod( 22, ( X + 1 ) );
        printf("%d\n",( a - 1 ) * (( b - 1 ) * 15) * ( c - 1 ) * 18 % 29) ;
    }
    return 0;
}  

全题：

Happy 2004

Time Limit:1000MS     Memory Limit:32768KB     64bit IO Format:%I64d & %I64u

Submit Status

Description

Consider a positive integer X,and let S be the sum of all positive integer divisors of 2004^X. Your job is to determine S modulo 29 (the rest of the division of S by 29).
Take X = 1 for an example. The positive integer divisors of 2004^1 are 1, 2, 3, 4, 6, 12, 167, 334, 501, 668, 1002 and 2004. Therefore S = 4704 and S modulo 29 is equal to 6.

Input

The input consists of several test cases. Each test case contains a line with the integer X (1 <= X <= 10000000).
A test case of X = 0 indicates the end of input, and should not be processed.

Output

For each test case, in a separate line, please output the result of S modulo 29.

Sample Input

1
10000
0

Sample Output

6
10