浅析强连通分量（Tarjan和kosaraju）

理解

  在有向图G中，如果两点互相可达，则称这两个点强连通，如果G中任意两点互相可达，则称G是强连通图。

定理： 1、一个有向图是强连通的，当且仅当G中有一个回路，它至少包含每个节点一次。

            2、非强连通有向图的极大强连通子图，称为强连通分量（SCC即Strongly Connected Componenet）。

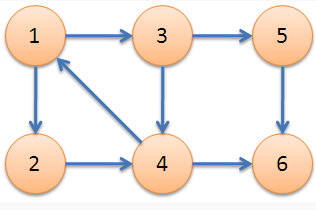
在上图中，{1,2,3,4}是一个强连通分量，{5}，{6}分别是另外两个强连通分量。怎么判断一个图是否是强连通图，如果不是，有哪些强连通分量，又怎么使它成为强连通图呢？

方法1：Korasaju算法

首先理解一下转置图的定义:将有向图G中的每一条边反向形成的图称为G的转置G ^T 。(注意到原图和G ^T 的强连通分支是一样的)

算法流程：

1.深度优先遍历G,算出每个结点u的结束时间f[u],起点如何选择无所谓。

2.深度优先遍历G的转置图G T ,选择遍历的起点时,按照结点的结束时间从大到小进行。遍历的过程中,一边遍历,一边给结点做分类标记,每找到一个新的起点,分类标记值就加1。

3. 第2步中产生的标记值相同的结点构成深度优先森林中的一棵树,也即一个强连通分量

注意：

　　Kosaraju算法比Tarjan时间复杂度要高，应用范围小，还有着爆栈超内存的风险，但这个算法比Tarjan好理解很多。当然和Tarjan一样，Kosaraju也只能用于有向图中。

　　Kosaraju也是基于深度优先搜索的算法。这个算法牵扯到两个概念，发现时间st，完成时间et。发现时间是指一个节点第一次被遍历到时的次序号，完成时间是指某一结点最后一次被遍历到的次序号。

　　在加边时把有向图正向建造完毕后再反向加边建一张逆图。

　　先对正图进行一遍dfs，遇到没访问过的点就让其发现时间等于目前的dfs次序号。在回溯时若发现某一结点的子树全部被遍历完，就让其完成时间等于目前dfs次序号。正图遍历完后将节点按完成时间入栈，保证栈顶是完成时间最大的节点，栈底是完成时间最小的节点。然后从栈顶开始向下每一个没有被反向遍历过的节点为起点对逆图进行一遍dfs，将访问到的点记录下来（或染色）并弹栈，每一遍反向dfs遍历到的点就构成一个强连通分量。

图解：

(a)为有向图G,
其中的阴影部分
是G的强连通分
支,对每个顶点
都标出了其发现
时刻与完成时刻
,黑色边为深度
优先搜索的树
枝;
(b)G的转置图G T
依次以b,c,g,h
为起点做DFS,
得到4个强连通
分量

算法复杂度分析

深度优先搜索的复杂度:Θ(V + E)

计算G T 的复杂度:0或者Θ(V + E)(临接表)
所以总的复杂度为:Θ(V + E)
非常好的算法!（个人更青睐于Tarjan，但kosaraju的思路至少得理解）

模板：

void positive_dfs(int pos){
    DFN++;
    vis[pos]=;
    for(int i=pre[][pos];i;i=E[][i].next)
        if(!vis[E[][i].to])
            positive_dfs(E[][i].to);
    stack[N*+-(++DFN)]=pos;
}
void negative_dfs(int pos){
    dye[pos]=CN;
    vis[pos]=;
    size[dye[pos]]++;
    for(int i=pre[][pos];i;i=E[][i].next)
        if(vis[E[][i].to])
            negative_dfs(E[][i].to);
}
int main(){

        ...... 

    for(int i=;i<=N;i++)
        if(!vis[i])
            positive_dfs(i);
    for(int i=;i<=N*;i++)
        if(stack[i]&&vis[stack[i]]){
            CN++;
            negative_dfs(stack[i]);
        }

        ......

}

方法二：Tarjan算法

理解：

　　Tarjan算法是基于对图深度优先搜索的算法，每个强连通分量为搜索树中的一棵子树。总的来说， Tarjan算法基于一个观察，即：同处于一个SCC中的结点必然构成DFS树的一棵子树。 我们要找SCC，就得找到它在DFS树上的根。

算法思想如下：

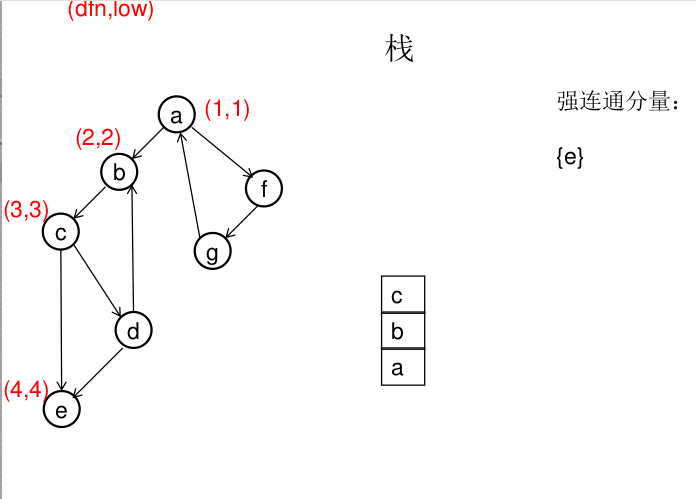
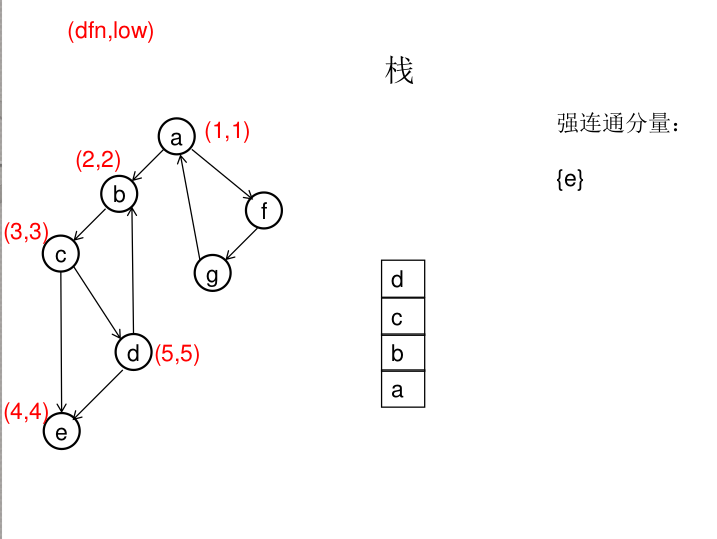
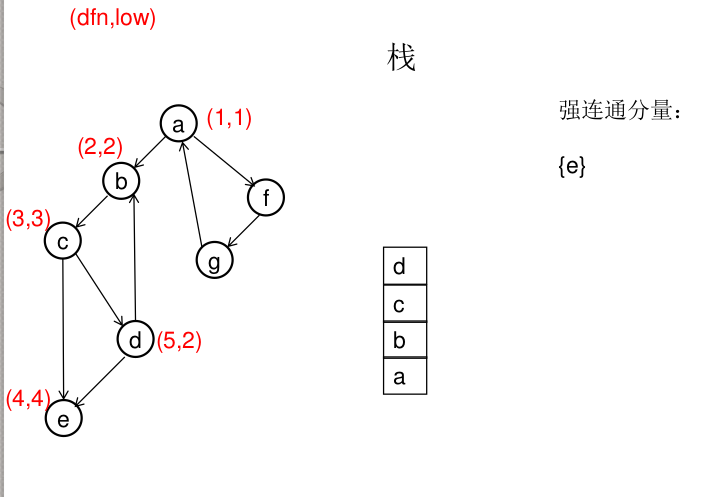
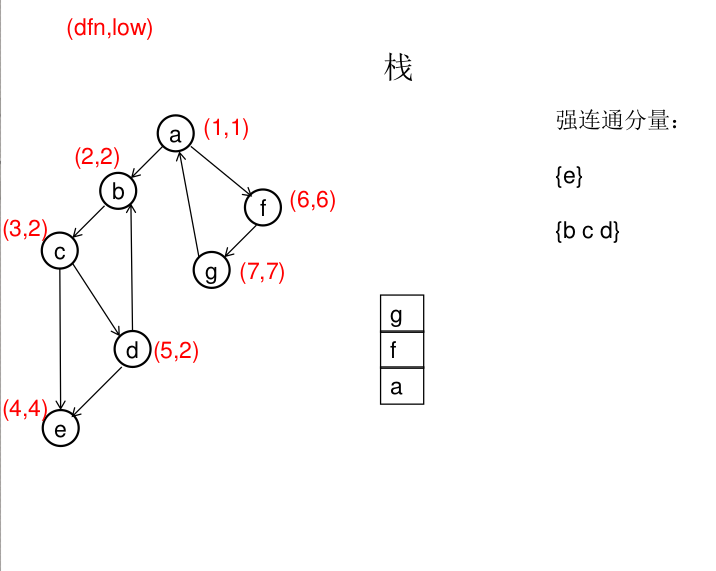
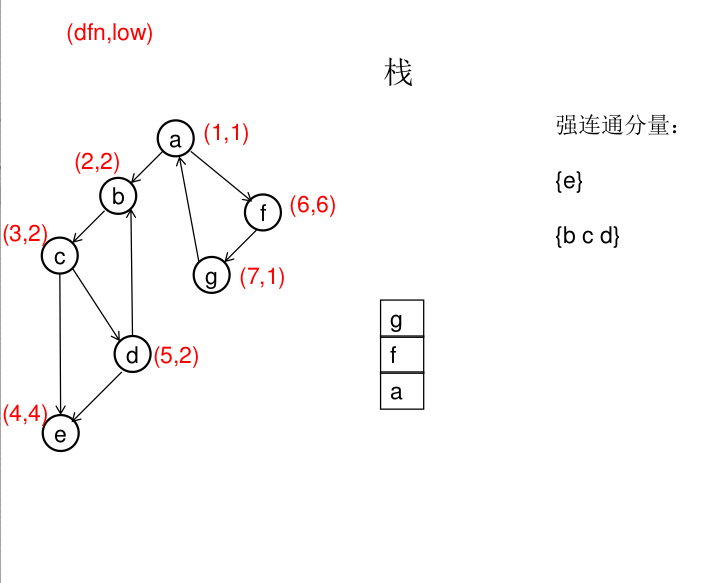
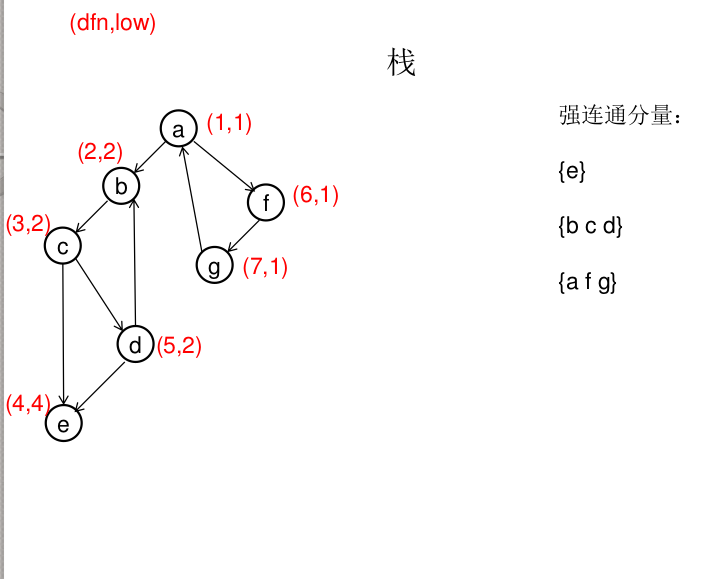
　　 dfn[u]表示dfs时达到顶点u的次序号（时间戳），low[u]表示以u为根节点的dfs树中次序号最小的顶点的次序号，所以当dfn[u]=low[u]时，以u为根的搜索子树上所有节点是一个强连通分量。 先将顶点u入栈，dfn[u]=low[u]=++idx,扫描u能到达的顶点v，如果v没有被访问过，则dfs(v)，low[u]=min(low[u],low[v])，如果v在栈里，low[u]=min(low[u],dfn[v])，扫描完v以后，如果dfn[u]=low[u]，则将u及其以上顶点出栈。

 图解（一定要仔细从左往右看）：

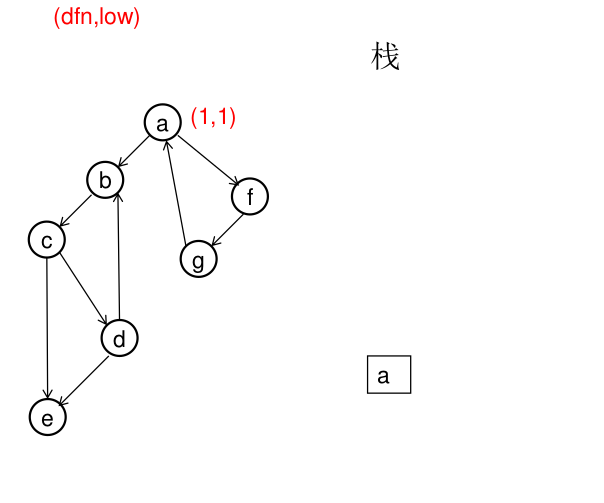
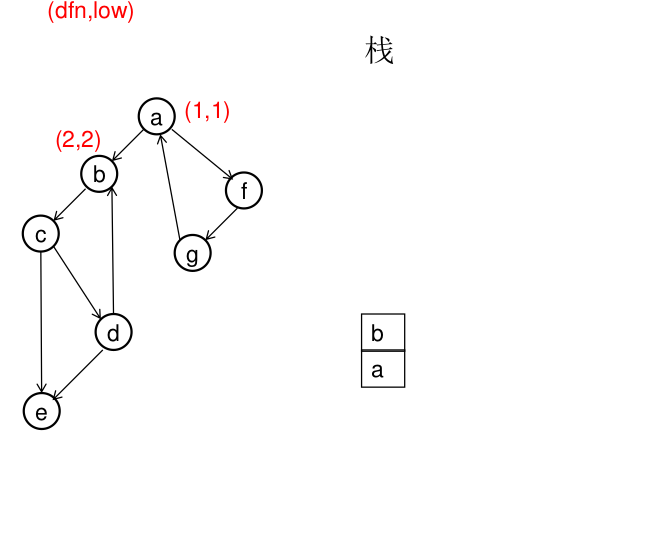
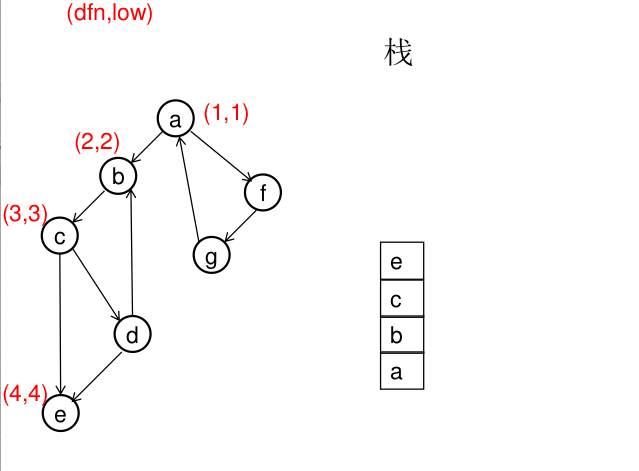
模板（Tarjan算法）：

void tarjan(int pos){
    vis[stack[++index]=pos]=;//入栈并标记
    LOW[pos]=DFN[pos]=++dfs_num;
    for(int i=pre[pos];i;i=E[i].next){
        if(!DFN[E[i].to]){
            tarjan(E[i].to);
            LOW[pos]=min(LOW[pos],LOW[E[i].to]);
        }
        else if(vis[E[i].to]) LOW[pos]=min(LOW[pos],DFN[E[i].to]);
    }
    if(LOW[pos]==DFN[pos]){
        vis[pos]=;
        size[dye[pos]=++CN]++;//染色及记录强连通分量大小
        while(pos!=stack[index]){
            vis[stack[index]]=;
            size[CN]++;//记录大小
            dye[stack[index--]]=CN;//弹栈并染色
        }
        index--;
    }
}

模板（完整Tarjan）：

#include <cstdio>
#include <stack>
#include <cstring>
#include <iostream>
using namespace std;
int n,m,idx=,k=,Bcnt=;
int head[];
int ins[]={};
int dfn[]={},low[]={};
int Belong[];
stack <int> s;
struct edge
{
    int v,next;
}e[];
int min(int a,int b)
{
    return a<b?a:b;
}
void adde(int u,int v)
{
     e[k].v=v;
     e[k].next=head[u];
     head[u]=k++;
}
void readdata()
{
     int a,b;
     memset(head,-,sizeof(head));
     scanf("%d%d",&n,&m);
     for(int i=;i<=m;i++)
     {
         scanf("%d%d",&a,&b);
         adde(a,b);
     }
}
void tarjan(int u)
{
     int v;
     dfn[u]=low[u]=++idx;//每次dfs，u的次序号增加1
     s.push(u);//将u入栈
     ins[u]=;//标记u在栈内
     for(int i=head[u];i!=-;i=e[i].next)//访问从u出发的边
     {
         v=e[i].v;
         if(!dfn[v])//如果v没被处理过
         {
             tarjan(v);//dfs(v)
             low[u]=min(low[u],low[v]);//u点能到达的最小次序号是它自己能到达点的最小次序号和连接点v能到达点的最小次序号中较小的
         }
         else if(ins[v])low[u]=min(low[u],dfn[v]);//如果v在栈内，u点能到达的最小次序号是它自己能到达点的最小次序号和v的次序号中较小的
     }
     if(dfn[u]==low[u])
     {
         Bcnt++;
         do
         {
             v=s.top();
             s.pop();
             ins[v]=;
             Belong[v]=Bcnt;
         }while(u != v);
     }
}
void work()
{
     for(int i=;i<=n;i++)if(!dfn[i])tarjan(i);
     printf("\n");
     for(int i = ;i <= ;i++)printf("%d %d\n",dfn[i],low[i]);
     printf("共有%d强连通分量，它们是:\n",Bcnt);
     for(int i=;i<=Bcnt;i++)
     {
        printf("第%d个:",i);
        for(int j=;j<=n;j++)
        {
           if(Belong[j]==i)printf("%d ",j);
        }
        printf("\n");
     }
}
int main()
{
    readdata();
    work();
    return ;
}
/*
6 8
1 2
1 3
2 4
3 4
3 5
4 1
4 6
5 6
*/

至于例题，～～博主太懒，自己去找吧，推荐codevs1332 上白泽慧音和洛谷 受欢迎的牛