二叉搜索树Java实现（查找、插入、删除、遍历）
由于最近想要阅读下 JDK1.8 中 HashMap 的具体实现，但是由于 HashMap 的实现中用到了红黑树，所以我觉得有必要先复习下红黑树的相关知识，所以写下这篇随笔备忘，有不对的地方请指出～
学习红黑树，我觉得有必要从二叉搜索树开始学起，本篇随笔就主要介绍 Java 实现二叉搜索树的查找、插入、删除、遍历等内容。
二叉搜索树需满足以下四个条件：
- 若任意节点的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
- 若任意节点的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
- 任意节点的左、右子树也分别为二叉查找树；
- 没有键值相等的节点。
二叉搜索树举例：
图一
接下来将基于图一介绍二叉搜索树相关操作。
首先，应先有一个节点对象相关的类，命名为 Node。
class Node {
int key;
int value;
Node leftChild;
Node rightChild;
public Node(int key, int value) {
this.key = key;
this.value = value;
}
public void displayNode() {
}
}
Node 类中包含 key 值，用于确定节点在树中相应位置，value 值代表要存储的内容，还含有指向左右孩子节点的两个引用。
接下来看下搜索树相应的类：
class Tree {
Node root;//保存树的根
public Node find(int key) {//查找指定节点
}
public void insert(int key, int value) {//插入节点
}
public boolean delete(int key) {//删除指定节点
}
private Node getDirectPostNode(Node delNode) {//得到待删除节点的直接后继节点
}
public void preOrder(Node rootNode) {//先序遍历树
}
public void inOrder(Node rootNode) {//中序遍历树
}
public void postOrder(Node rootNode) {//后序遍历树
}
}
类中表示树的框架，包含查找、插入、遍历、删除相应方法，其中删除节点操作最为复杂，接下来一一介绍。
一、查找某个节点
由于二叉搜索树定义上的特殊性，只需根据输入的 key 值从根开始进行比较，若小于根的 key 值，则与根的左子树比较，大于根的key值与根的右子树比较，以此类推，找到则返回相应节点，否则返回 null。
public Node find(int key) {
Node currentNode = root;
while (currentNode != null && currentNode.key != key) {
if (key < currentNode.key) {
currentNode = currentNode.leftChild;
} else {
currentNode = currentNode.rightChild;
}
}
return currentNode;
}
二、插入节点
与查找操作相似，由于二叉搜索树的特殊性，待插入的节点也需要从根节点开始进行比较，小于根节点则与根节点左子树比较，反之则与右子树比较，直到左子树为空或右子树为空，则插入到相应为空的位置，在比较的过程中要注意保存父节点的信息 及 待插入的位置是父节点的左子树还是右子树，才能插入到正确的位置。
public void insert(int key, int value) {
if (root == null) {
root = new Node(key, value);
return;
}
Node currentNode = root;
Node parentNode = root;
boolean isLeftChild = true;
while (currentNode != null) {
parentNode = currentNode;
if (key < currentNode.key) {
currentNode = currentNode.leftChild;
isLeftChild = true;
} else {
currentNode = currentNode.rightChild;
isLeftChild = false;
}
}
Node newNode = new Node(key, value);
if (isLeftChild) {
parentNode.leftChild = newNode;
} else {
parentNode.rightChild = newNode;
}
}
三、遍历二叉搜索树
遍历操作与遍历普通二叉树操作完全相同，不赘述。
public void preOrder(Node rootNode) {
if (rootNode != null) {
System.out.println(rootNode.key + " " + rootNode.value);
preOrder(rootNode.leftChild);
preOrder(rootNode.rightChild);
}
}
public void inOrder(Node rootNode) {
if (rootNode != null) {
inOrder(rootNode.leftChild);
System.out.println(rootNode.key + " " + rootNode.value);
inOrder(rootNode.rightChild);
}
}
public void postOrder(Node rootNode) {
if (rootNode != null) {
postOrder(rootNode.leftChild);
postOrder(rootNode.rightChild);
System.out.println(rootNode.key + " " + rootNode.value);
}
}
四、删除指定节点。
在二叉搜索树中删除节点操作较复杂，可分为以下三种情况。
1、待删除的节点为叶子节点，可直接删除。
public boolean delete(int key) {
Node currentNode = root;//用来保存待删除节点
Node parentNode = root;//用来保存待删除节点的父亲节点
boolean isLeftChild = true;//用来确定待删除节点是父亲节点的左孩子还是右孩子
while (currentNode != null && currentNode.key != key) {
parentNode = currentNode;
if (key < currentNode.key) {
currentNode = currentNode.leftChild;
isLeftChild = true;
} else {
currentNode = currentNode.rightChild;
isLeftChild = false;
}
}
if (currentNode == null) {
return false;
}
if (currentNode.leftChild == null && currentNode.rightChild == null) {//要删除的节点为叶子节点
if (currentNode == root)
root = null;
else if (isLeftChild)
parentNode.leftChild = null;
else
parentNode.rightChild = null;
}
......
}
2、待删除节点只有一个孩子节点
例如删除图一中的 key 值为 11 的节点，只需将 key 值为 13 的节点的左孩子指向 key 值为 12的节点即可达到删除 key 值为 11 的节点的目的。
由以上分析可得代码如下（接上述 delete 方法省略号后）：
else if (currentNode.rightChild == null) {//要删除的节点只有左孩子
if (currentNode == root)
root = currentNode.leftChild;
else if (isLeftChild)
parentNode.leftChild = currentNode.leftChild;
else
parentNode.rightChild = currentNode.leftChild;
} else if (currentNode.leftChild == null) {//要删除的节点只有右孩子
if (currentNode == root)
root = currentNode.rightChild;
else if (isLeftChild)
parentNode.leftChild = currentNode.rightChild;
else
parentNode.rightChild = currentNode.rightChild;
}
......
3、待删除节点既有左孩子，又有右孩子。
例如删除图一中 key 值为 10 的节点，这时就需要用 key 值为 10 的节点的中序后继节点（节点 11）来代替 key 值为 10 的节点，并删除 key 值为 10 的节点的中序后继节点，由中序遍历相关规则可知， key 值为 10 的节点的直接中序后继节点一定是其右子树中 key 值最小的节点，所以此中序后继节点一定不含子节点或者只含有一个右孩子，删除此中序后继节点就属于上述 1,2 所述情况。图一中 key 值为 10 的节点的直接中序后继节点 为 11，节点 11 含有一个右孩子 12。
所以删除 图一中 key 值为 10 的节点分为以下几步：
a、找到 key 值为 10 的节点的直接中序后继节点（即其右子树中值最小的节点 11），并删除此直接中序后继节点。
private Node getDirectPostNode(Node delNode) {//方法作用为得到待删除节点的直接后继节点
Node parentNode = delNode;//用来保存待删除节点的直接后继节点的父亲节点
Node direcrPostNode = delNode;//用来保存待删除节点的直接后继节点
Node currentNode = delNode.rightChild;
while (currentNode != null) {
parentNode = direcrPostNode;
direcrPostNode = currentNode;
currentNode = currentNode.leftChild;
}
if (direcrPostNode != delNode.rightChild) {//从树中删除此直接后继节点
parentNode.leftChild = direcrPostNode.rightChild;
direcrPostNode.rightChild = null;
}
return direcrPostNode;//返回此直接后继节点
}
b、将此后继节点的 key、value 值赋给待删除节点的 key，value值。(接情况二中省略号代码之后)
else { //要删除的节点既有左孩子又有右孩子
//思路：用待删除节点右子树中的key值最小节点的值来替代要删除的节点的值,然后删除右子树中key值最小的节点
//右子树key最小的节点一定不含左子树,所以删除这个key最小的节点一定是属于叶子节点或者只有右子树的节点
Node directPostNode = getDirectPostNode(currentNode);
currentNode.key = directPostNode.key;
currentNode.value = directPostNode.value;
}
至此删除指定节点的操作结束。
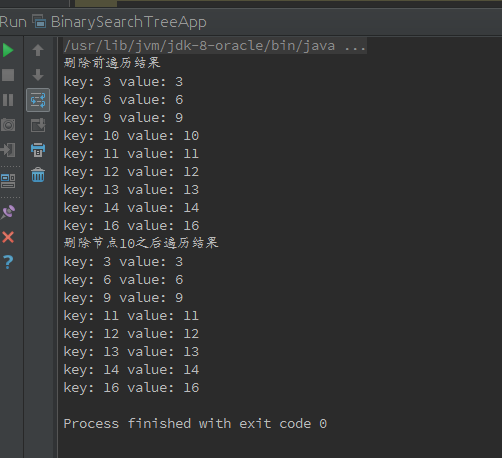
最后给出完整代码及简单测试代码及测试结果：
class Node {
int key;
int value;
Node leftChild;
Node rightChild;
public Node(int key, int value) {
this.key = key;
this.value = value;
}
public void displayNode() {
}
}
class Tree {
Node root;
public Node find(int key) {
Node currentNode = root;
while (currentNode != null && currentNode.key != key) {
if (key < currentNode.key) {
currentNode = currentNode.leftChild;
} else {
currentNode = currentNode.rightChild;
}
}
return currentNode;
}
public void insert(int key, int value) {
if (root == null) {
root = new Node(key, value);
return;
}
Node currentNode = root;
Node parentNode = root;
boolean isLeftChild = true;
while (currentNode != null) {
parentNode = currentNode;
if (key < currentNode.key) {
currentNode = currentNode.leftChild;
isLeftChild = true;
} else {
currentNode = currentNode.rightChild;
isLeftChild = false;
}
}
Node newNode = new Node(key, value);
if (isLeftChild) {
parentNode.leftChild = newNode;
} else {
parentNode.rightChild = newNode;
}
}
public boolean delete(int key) {
Node currentNode = root;
Node parentNode = root;
boolean isLeftChild = true;
while (currentNode != null && currentNode.key != key) {
parentNode = currentNode;
if (key < currentNode.key) {
currentNode = currentNode.leftChild;
isLeftChild = true;
} else {
currentNode = currentNode.rightChild;
isLeftChild = false;
}
}
if (currentNode == null) {
return false;
}
if (currentNode.leftChild == null && currentNode.rightChild == null) {
//要删除的节点为叶子节点
if (currentNode == root)
root = null;
else if (isLeftChild)
parentNode.leftChild = null;
else
parentNode.rightChild = null;
} else if (currentNode.rightChild == null) {//要删除的节点只有左孩子
if (currentNode == root)
root = currentNode.leftChild;
else if (isLeftChild)
parentNode.leftChild = currentNode.leftChild;
else
parentNode.rightChild = currentNode.leftChild;
} else if (currentNode.leftChild == null) {//要删除的节点只有右孩子
if (currentNode == root)
root = currentNode.rightChild;
else if (isLeftChild)
parentNode.leftChild = currentNode.rightChild;
else
parentNode.rightChild = currentNode.rightChild;
} else { //要删除的节点既有左孩子又有右孩子
//思路：用待删除节点右子树中的key值最小节点的值来替代要删除的节点的值,然后删除右子树中key值最小的节点
//右子树key最小的节点一定不含左子树,所以删除这个key最小的节点一定是属于叶子节点或者只有右子树的节点
Node directPostNode = getDirectPostNode(currentNode);
currentNode.key = directPostNode.key;
currentNode.value = directPostNode.value;
}
return true;
}
private Node getDirectPostNode(Node delNode) {//方法作用为得到待删除节点的直接后继节点
Node parentNode = delNode;//用来保存待删除节点的直接后继节点的父亲节点
Node direcrPostNode = delNode;//用来保存待删除节点的直接后继节点
Node currentNode = delNode.rightChild;
while (currentNode != null) {
parentNode = direcrPostNode;
direcrPostNode = currentNode;
currentNode = currentNode.leftChild;
}
if (direcrPostNode != delNode.rightChild) {//从树中删除此直接后继节点
parentNode.leftChild = direcrPostNode.rightChild;
direcrPostNode.rightChild = null;
}
return direcrPostNode;//返回此直接后继节点
}
public void preOrder(Node rootNode) {
if (rootNode != null) {
System.out.println(rootNode.key + " " + rootNode.value);
preOrder(rootNode.leftChild);
preOrder(rootNode.rightChild);
}
}
public void inOrder(Node rootNode) {
if (rootNode != null) {
inOrder(rootNode.leftChild);
System.out.println("key: " + rootNode.key + " " + "value: " + rootNode.value);
inOrder(rootNode.rightChild);
}
}
public void postOrder(Node rootNode) {
if (rootNode != null) {
postOrder(rootNode.leftChild);
postOrder(rootNode.rightChild);
System.out.println(rootNode.key + " " + rootNode.value);
}
}
private void destroy(Node tree) {
if (tree==null)
return ;
if (tree.left != null)
destroy(tree.leftChild);
if (tree.right != null)
destroy(tree.rightChild);
tree=null;
}
public void destory() {
destory(root);
}
}
public class BinarySearchTreeApp {
150 public static void main(String[] args) {
151 Tree tree = new Tree();
152 tree.insert(6, 6);//插入操作,构造图一所示的二叉树 153 tree.insert(3, 3); tree.insert(14, 14); 155 tree.insert(16, 16); 156 tree.insert(10, 10); 157 tree.insert(9, 9); tree.insert(13, 13); 159 tree.insert(11, 11); tree.insert(12, 12); 162 System.out.println("删除前遍历结果"); tree.inOrder(tree.root);//中序遍历操作 165 System.out.println("删除节点10之后遍历结果"); tree.delete(10);//删除操作 tree.inOrder(tree.root);
} }
测试结果：
二叉搜索树Java实现（查找、插入、删除、遍历）的更多相关文章
- PTA L2-004 这是二叉搜索树吗？-判断是否是对一棵二叉搜索树或其镜像进行前序遍历的结果 团体程序设计天梯赛-练习集
L2-004 这是二叉搜索树吗? (25 分) 一棵二叉搜索树可被递归地定义为具有下列性质的二叉树:对于任一结点, 其左子树中所有结点的键值小于该结点的键值: 其右子树中所有结点的键值大于等于该结 ...
- 二叉搜索树(Java实现)
二叉搜索树基本操作 求树中的结点个数 判断节点是否为空 向树中插入新结点key-value 树中是否存在key 返回树中key对应的value值 先序遍历 中序遍历 后续遍历 层序遍历 求树中key最 ...
- 在二叉搜索树(BST)中查找第K个大的结点之非递归实现
一个被广泛使用的面试题: 给定一个二叉搜索树,请找出其中的第K个大的结点. PS:我第一次在面试的时候被问到这个问题而且让我直接在白纸上写的时候,直接蒙圈了,因为没有刷题准备,所以就会有伤害.(面完的 ...
- leetcode- 将有序数组转换为二叉搜索树(java)
将一个按照升序排列的有序数组,转换为一棵高度平衡二叉搜索树. 本题中,一个高度平衡二叉树是指一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1. 示例: 给定有序数组: [-10,-3,0, ...
- [LC]783题 二叉搜索树结点最小距离（中序遍历）
①题目 给定一个二叉搜索树的根结点 root, 返回树中任意两节点的差的最小值. 示例: 输入: root = [4,2,6,1,3,null,null]输出: 1解释:注意,root是树结点对象(T ...
- [LeetCode] 538. 把二叉搜索树转换为累加树 ☆(中序遍历变形)
把二叉搜索树转换为累加树 描述 给定一个二叉搜索树(Binary Search Tree),把它转换成为累加树(Greater Tree),使得每个节点的值是原来的节点值加上所有大于它的节点值之和. ...
- 数据结构-二叉搜索树Java实现
1,Node.java 生成基础二叉树的结构 package com.cnblogs.mufasa.searchTree; /** * 节点配置父+左+右 */ public class Node{ ...
- Java实现二叉搜索树的插入、删除
前置知识 二叉树的结构 public class TreeNode { int val; TreeNode left; TreeNode right; TreeNode() { } TreeNode( ...
- 二叉搜索树、AVL平衡二叉搜索树、红黑树、多路查找树
1.二叉搜索树 1.1定义 是一棵二叉树,每个节点一定大于等于其左子树中每一个节点,小于等于其右子树每一个节点 1.2插入节点 从根节点开始向下找到合适的位置插入成为叶子结点即可:在向下遍历时,如果要 ...
随机推荐
- mac 访问mysql客户端
/usr/local/mysql/bin/mysql -u root -p //mac mysql 管理工具推荐 sequek pro
- linux动态链接库---一篇讲尽
一般我们在Linux下执行某些外部程序的时候可能会提示找不到共享库的错误, 比如: tmux: error while loading shared libraries: libevent-1.4.s ...
- stm32-ucos移植lwip-1（raw）
之前在裸机环境下移植了lwip,功能还是很强大的,但是就我看来,这和uip其实差别也不大,其实lwip更强大的功能需要在操作系统之下才能发挥出来,今天就来做这个 首先我们需要移植操作系统,系统选择uc ...
- SpringMVC强大的数据绑定（2）——第六章 注解式控制器详解
SpringMVC强大的数据绑定(2)——第六章 注解式控制器详解 博客分类: 跟开涛学SpringMVC 6.6.2.@RequestParam绑定单个请求参数值 @RequestParam用于 ...
- leetcode--007 word break I
aaarticlea/png;base64,iVBORw0KGgoAAAANSUhEUgAAA+4AAAC5CAIAAAA55fI7AAAZa0lEQVR4nO3dPW7bQIMG4L2MT6B7+A
- java实现——030最小的k个数
1.O(nlogk)海量数据 import java.util.TreeSet; public class T030 { public static void main(String[] args){ ...
- ndk-stack 调试 android c++ 代码崩溃位置
在android下面使用jni来调用c++,在开发游戏是非常正常的.但是要调试c++部分却是非常麻烦的问题.如果快速定位崩溃位置呢.NDK提供了一个小工具ndk-stack. 首先,我们先配置环境,把 ...
- diff命令参数
diff命令参数: diff - 找出两个文件的不同点 总览 diff [选项] 源文件 目标文件 描述 在最简单的情况是, diff 比较两个文件的内容 (源文件 和 目标文件). 文件名可以是 - ...
- java web面试
1. session和cookie的区别和联系,session的生命周期,多个服务部署时session管理. 原博http://blog.csdn.net/shuaishenkkk/article/d ...
- iOS bug 之 H5 页面没有弹出提示框
描述:在安卓上有提示框,但是在iOS上没有提示框. step 1: 失误,是我没有在正确的位置设置网址. step 2: 修改之后,测试页能弹出提示框,但是正式的页面没有提示框. step 3: 我输 ...