前缀树（Tire）—Python

核心思想

空间换时间，是一种用于快速减速的多叉树结构，利用字符串的公共前缀来降低时间

优缺点：

优点：查询效率高，减少字符比较

缺点：内存消耗较大

每次都会从头向下一直到字符串结尾

前缀树

1 单个字符串从前到后加到一棵多叉树上

2 每隔字符串都会有自己所在节点的两个属性path和end，path代表经过，end代表这个字符结尾

3 所有的插入操作都是一样的插入方式，有就复用没有就新开辟一条路

4 经过节点path += 1 ；每个字符串结尾 end += 1

5 可以快速查询前缀和完全匹配的数量

画图解释

如图所示 我们插入第一个字符串“abc”，从a开始，没有a就开辟一个a的路把经过的地方都标记path += 1

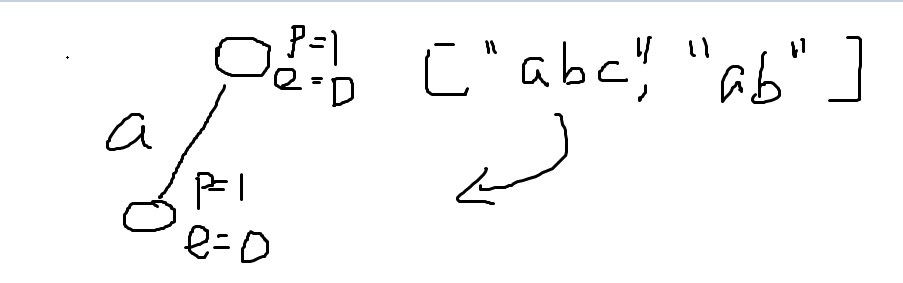
结果相同方式遍历b和c，最后c结果end +=1

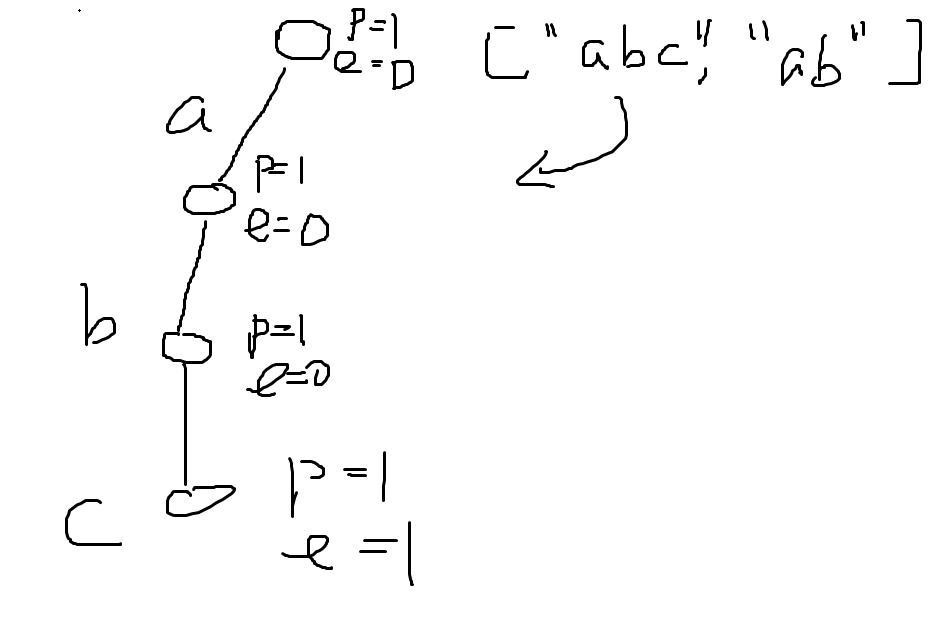
相同的方式插入ab，每次都会从头开始第一个起始点path += 1，a存在a的path += 1，b也存在b的path +=1 ，b是结尾所以b的end +=1

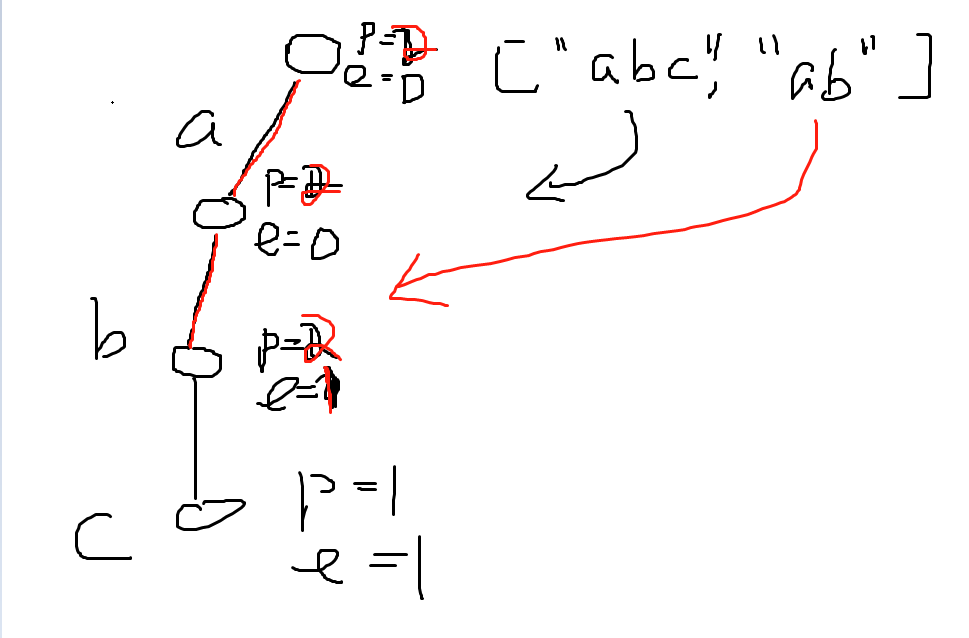
实现

两种方式实现，第一种会用列表来储存，一种会用字典来储存

实现方式都一样，看会一种即可。

第一种

class Trie:

    def __init__(self):
        """
        Initialize your data structure here.
        """
        self.children = [None] * 26
        self.path = 0
        self.isEnd = 0

    def insert(self, word: str) -> None:
        """
        Inserts a word into the trie.
        """
        node = self
        node.path += 1
        for ch in word:
            offset = ord(ch) - ord('a')
            # node.path += 1
            if not node.children[offset]:
                node.children[offset] = Trie()
            node = node.children[offset]
            node.path += 1

        node.isEnd += 1

    def startsWith(self, prefix: str) :
        node = self
        for ch in prefix:
            offset = ord(ch) - ord('a')
            if not node.children[offset]:
                return None
            node = node.children[offset]

        return node.path

    def search(self, prefix: str) :
        node = self
        for ch in prefix:
            offset = ord(ch) - ord('a')
            if not node.children[offset]:
                return None
            node = node.children[offset]

        return node.isEnd

第二种

class Trie:

    def __init__(self):
        """
        Initialize your data structure here.
        """
        self.children = dict()
        self.path = 0
        self.isEnd = 0

    def insert(self, word: str) -> None:
        """
        Inserts a word into the trie.
        """
        node = self
        node.path += 1
        for ch in word:
            offset = ord(ch) - ord('a')
            if offset not in node.children:
                node.children[offset] = Trie()
            node = node.children[offset]
            node.path += 1

        node.isEnd += 1

    def startsWith(self, prefix: str) :
        node = self
        for ch in prefix:
            offset = ord(ch) - ord('a')
            if offset not in node.children:
                return None
            node = node.children[offset]

        return node.path

    def search(self, prefix: str) :
        node = self
        for ch in prefix:
            offset = ord(ch) - ord('a')
            if offset not in node.children:
                return None
            node = node.children[offset]

        return node.isEnd