1. 矩阵分解可以用来解决什么方法, 以及how?

利用矩阵分解来解决实际问题的分析方法很多，如PCA(主成分分析)、ICA(独立成分分析)、SVD(奇异值分解)、VQ(矢量量化)等。在所有这些方法中，原始的大矩阵V被近似分解为低秩的V=WH形式。这些方法的共同特点是，因子W和H中的元素可为正或负，即使输入的初始矩阵元素是全正的，传统的秩削减算法也不能保证原始数据的非负性。在数学上，从计算的观点看，分解结果中存在负值是正确的，但负值元素在实际问题中往往是没有意义的。例如图像数据中不可能有负值的像素点；在文档统计中，负值也是无法解释的。
2. NMF

NMF的基本思想可以简单描述为：对于任意给定的一个非负矩阵A，NMF算法能够寻找到一个非负矩阵U和一个非负矩阵V，使得满足 ，从而将一个非负的矩阵分解为左右两个非负矩阵的乘积。

分解前后可理解为：原始矩阵的列向量是对左矩阵中所有列向量的加权和，而权重系数就是右矩阵对应列向量的元素，故称为基矩阵，为系数矩阵。一般情况下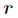的选择要比小，即满足，这时用系数矩阵代替原始矩阵，就可以实现对原始矩阵进行降维，得到数据特征的降维矩阵，从而减少存储空间，减少计算机资源。

other documentations: NMF 非负矩阵分解 -- 原理与应用

Supplementary knowledge

1. matrix rank矩阵的秩

NMF: non-negative matrix factorization.的更多相关文章

  1. 关于NMF（Non-negative Matrix Factorization ）

    著名的科学杂志<Nature>于1999年刊登了两位科学家D.D.Lee和H.S.Seung对数学中非负矩阵研究的突出成果.该文提出了一种新的矩阵分解思想――非负矩阵分解(Non-nega ...

  2. Matrix Factorization, Algorithms, Applications, and Avaliable packages

    矩阵分解 来源:http://www.cvchina.info/2011/09/05/matrix-factorization-jungle/ 美帝的有心人士收集了市面上的矩阵分解的差点儿全部算法和应 ...

  3. 《Non-Negative Matrix Factorization for Polyphonic Music Transcription》译文

    NMF(非负矩阵分解),由于其分解出的矩阵是非负的,在一些实际问题中具有非常好的解释,因此用途很广.在此,我给大家介绍一下NMF在多声部音乐中的应用.要翻译的论文是利用NMF转录多声部音乐的开山之作, ...

  4. Non-negative Matrix Factorization 非负矩阵分解

    著名的科学杂志<Nature>于1999年刊登了两位科学家D.D.Lee和H.S.Seung对数学中非负矩阵研究的突出成果.该文提出了一种新的矩阵分解思想――非负矩阵分解(Non-nega ...

  5. Matrix Factorization SVD 矩阵分解

    Today we have learned the Matrix Factorization, and I want to record my study notes. Some kownledge ...

  6. 机器学习技法：15 Matrix Factorization

    Roadmap Linear Network Hypothesis Basic Matrix Factorization Stochastic Gradient Descent Summary of ...

  7. 机器学习技法笔记：15 Matrix Factorization

    Roadmap Linear Network Hypothesis Basic Matrix Factorization Stochastic Gradient Descent Summary of ...

  8. 【RS】Sparse Probabilistic Matrix Factorization by Laplace Distribution for Collaborative Filtering - 基于拉普拉斯分布的稀疏概率矩阵分解协同过滤

    [论文标题]Sparse Probabilistic Matrix Factorization by Laplace Distribution for Collaborative Filtering  ...

  9. 【RS】List-wise learning to rank with matrix factorization for collaborative filtering - 结合列表启发排序和矩阵分解的协同过滤

    [论文标题]List-wise learning to rank with matrix factorization for collaborative filtering   (RecSys '10 ...

  10. 【RS】Matrix Factorization Techniques for Recommender Systems - 推荐系统的矩阵分解技术

    [论文标题]Matrix Factorization Techniques for Recommender Systems(2009,Published by the IEEE Computer So ...

随机推荐

  1. Bash脚本编程学习笔记04：测试命令test、状态返回值、位置参数和特殊变量

    我自己接触Linux主要是大学学习的Turbolinux --> 根据<鸟哥的Linux私房菜:基础篇>(第三版) --> 马哥的就业班课程.给我的感觉是这些课程对于bash的 ...

  2. docker搭建环境积累

    weblogic12搭建 sudo docker pull ismaleiva90/weblogic12 sudo docker run -d -p : -p : ismaleiva90/weblog ...

  3. Mac IDEA 2019.3.1下载及破解，可激活至2089年

    背景 目前IDEA已更新到2019.3.3,但是下载这个版本后使用目前网上的常见破解方法会出现各种问题.比如使用注册码方式提示license key is in legacy format,或者使用L ...

  4. 论文阅读笔记（十七）【ICCV2017】：Dynamic Label Graph Matching for Unsupervised Video Re-Identification

    Introduction 文章主要提出了 Dynamic Graph Matching(DGM)方法,以非监督的方式对多个相机的行人视频中识别出正确匹配.错误匹配的结果.本文主要思想如下图: 具体而言 ...

  5. 聊聊智能指针 auto_ptr、shared_ptr、weak_ptr和unique_ptr

    本文为转载:https://www.cnblogs.com/zeppelin5/p/10083597.html,对作者有些地方做了修正. 手写代码是理解C++的最好办法,以几个例子说明C++四个智能指 ...

  6. 网络共享服务(二)之NFS

    NFS: Network File System,是一种基于TCP/IP传输的网络文件系统协议,最初由SUN公司开发.通过使用NFS协议,客户机可以像访问本地目录一样访问服务器中的共享资源.但是,NF ...

  7. oracle基础知识点

    一.count(*).count(1).count(字段名)的区别select count(*) from t_md_inst --153797 --包含字段为null 的记录select count ...

  8. 最简单的githut操作命令

    创建SSH Key: 参考:https://blog.csdn.net/weixin_30345055/article/details/95139358 在用户目录下,看看有没有.ssh文件夹,如果有 ...

  9. 【巨杉数据库SequoiaDB】为“战疫” 保驾护航，巨杉在行动

    2020年,我们经历了一个不平静的新春,在这场大的“战疫”中,巨杉数据库也积极响应号召,勇于承担新一代科技企业的社会担当,用自己的行动助力这场疫情防控阻击战! 赋能“战疫”快速响应 巨杉数据库目前服务 ...

  10. Navicat 安装+连接

    Navicat安装包: 链接:https://pan.baidu.com/s/1bvKagRJ0w_7LH0t4597ycA 提取码:yftv 如MySQL 8.0+ 安装成功后,教程见本博 可用Na ...