线段拟合(带拉格朗日乘子,HGL)
线段特征上的扫描点满足 (1)。本文的线段特征定义为:L: [dL, φL, PLs, PLe]T,如图1所示。其中,dL为笛卡尔坐标系中原点(激光传感器所在位置)到线段的距离, φL为线段特征的倾角,PLs为线段特征起点,PLe为线段特征终点。线段特征在笛卡尔坐标系下方程为:
 (1)
(1)
其中,dL > 0,-π < φL < π,xi = ρicosφi,yi = ρisinφi。
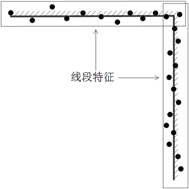
图1 线段
前几节中,通过统计学方法划分出若干区域,为了准确提取线段特征,采用带约束的最小二乘法对每个划分区域特征进行特征提取,将(1)式转换为如下形式:
 (2)
(2)
式中 S、E——线段端点。
将上式改写为矩阵形式有:
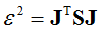 (3)
(3)
其中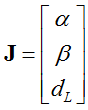 ,
,  ,
,  ,
,  。由于α2+β2=1,引入拉格朗日乘子λ,得:
。由于α2+β2=1,引入拉格朗日乘子λ,得:
 (4)
(4)
其中,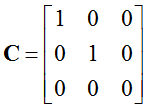 ,满足JTCJ=1。令
,满足JTCJ=1。令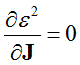 ,得:
,得:
 (5)
(5)
解上式的广义特征值与广义特征向量,S为一个正定矩阵,待求特征向量J一定对应最小的特征值λ。当α与β确定以后,可以求得:
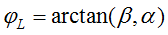 (6)
(6)
然后,求出线段特征dL。最后,转换到全局坐标系下。
文献[1]给出了一种误差传播方法,通过最小化隐含的关系方程F(I,O),给出最终误差(I输入误差,O输出误差)。将误差扩展到协方差矩阵,可以通过输入的协方差矩阵ΣI,得到输出的协方差矩阵ΣL。则有:
 (7)
(7)
其中, 。
。 ,
,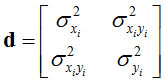 令:
令:
 (8)
(8)
代入最后计算出ΣL。
[1] Haralick R M. Propagating covariance in computer vision[M]. Performance Characterization in Computer Vision. Springer Netherlands, 2000: 95-114.
线段拟合(带拉格朗日乘子,HGL)的更多相关文章
- 关于拉格朗日乘子法和KKT条件
解密SVM系列(一):关于拉格朗日乘子法和KKT条件 标签: svm算法支持向量机 2015-08-17 18:53 1214人阅读 评论(0) 收藏 举报 分类: 模式识别&机器学习(42 ...
- 装载:关于拉格朗日乘子法与KKT条件
作者:@wzyer 拉格朗日乘子法无疑是最优化理论中最重要的一个方法.但是现在网上并没有很好的完整介绍整个方法的文章.我这里尝试详细介绍一下这方面的有关问题,插入自己的一些理解,希望能够对大家有帮助. ...
- 约束优化方法之拉格朗日乘子法与KKT条件
引言 本篇文章将详解带有约束条件的最优化问题,约束条件分为等式约束与不等式约束,对于等式约束的优化问题,可以直接应用拉格朗日乘子法去求取最优值:对于含有不等式约束的优化问题,可以转化为在满足 KKT ...
- 机器学习笔记——拉格朗日乘子法和KKT条件
拉格朗日乘子法是一种寻找多元函数在一组约束下的极值方法,通过引入拉格朗日乘子,可将有m个变量和n个约束条件的最优化问题转化为具有m+n个变量的无约束优化问题.在介绍拉格朗日乘子法之前,先简要的介绍一些 ...
- 真正理解拉格朗日乘子法和 KKT 条件
这篇博文中直观上讲解了拉格朗日乘子法和 KKT 条件,对偶问题等内容. 首先从无约束的优化问题讲起,一般就是要使一个表达式取到最小值: \[min \quad f(x)\] 如 ...
- 关于拉格朗日乘子法与KKT条件
关于拉格朗日乘子法与KKT条件 关于拉格朗日乘子法与KKT条件 目录 拉格朗日乘子法的数学基础 共轭函数 拉格朗日函数 拉格朗日对偶函数 目标函数最优值的下界 拉格朗日对偶函数与共轭函数的联系 拉 ...
- 拉格朗日乘子法 - KKT条件 - 对偶问题
接下来准备写支持向量机,然而支持向量机和其他算法相比牵涉较多的数学知识,其中首当其冲的就是标题中的拉格朗日乘子法.KKT条件和对偶问题,所以本篇先作个铺垫. 大部分机器学习算法最后都可归结为最优化问题 ...
- 支持向量机(SVM)必备概念(凸集和凸函数,凸优化问题,软间隔,核函数,拉格朗日乘子法,对偶问题,slater条件、KKT条件)
SVM目前被认为是最好的现成的分类器,SVM整个原理的推导过程也很是复杂啊,其中涉及到很多概念,如:凸集和凸函数,凸优化问题,软间隔,核函数,拉格朗日乘子法,对偶问题,slater条件.KKT条件还有 ...
- 机器学习——支持向量机(SVM)之拉格朗日乘子法,KKT条件以及简化版SMO算法分析
SVM有很多实现,现在只关注其中最流行的一种实现,即序列最小优化(Sequential Minimal Optimization,SMO)算法,然后介绍如何使用一种核函数(kernel)的方式将SVM ...
随机推荐
- filter 静态资源
package com.itheima.web.filter; import java.io.IOException; import javax.servlet.Filter; import java ...
- JAVA 中 if和while的区别
while和if本身就用法不同,一个是循环语句,一个是判断语句. if 只做判断,判断一次之后,便不会再回来了while 的话,循环,直到结果为false,才跳出来 链表的结构,要一直读下去,直到读完 ...
- 读书笔记-NIO的工作方式
读书笔记-NIO的工作方式 1.BIO是阻塞IO,一旦阻塞线程将失去对CPU的使用权,当前的网络IO有一些解决办法:1)一个客户端对应一个处理线程:2)采用线程池.但也会出问题. 2.NIO的关键类C ...
- innosetup卸载软件后,删除定时任务schedule task
代码如下: //innosetup自带的方法,当卸载软件时,根据卸载的状态改变时而触发 procedure CurUninstallStepChanged(CurUninstallStep: TUni ...
- java 读写操作大文件 BufferedReader和RandomAccessFile
一 老问这问题,两个都答出来算加分项? 二 具体代码如下,没什么好说的直接说对比. BufferedReader和RandomAccessFile的区别RandomAccessFile 在数据越大,性 ...
- C# 定制特性
一.初识特性 特性(attribute)是被指定给某一声明的一则附加的声明性信息. 设计类型的时候可以使用各种成员来描述该类型的信息,但有时候我们可能不太愿意将一些附加信息放到类的内部,因为这样,可能 ...
- 前端测试框架 puppeteer 文档翻译
puppeteer puppeteer 是一个通过DevTools 协议提供高级API 来控制 chrome,chromium 的 NODE库; puppeteer默认运行在 headless 模式, ...
- 获取当前的日期时间的js函数,格式为“yyyy-MM-dd hh:mm:ss”
//获取当前的日期时间函数,格式为“yyyy-MM-dd hh:mm:ss” function getNowFormatDate(date) { if (date == null) { var dat ...
- java项目升级spring4.3.x 、jdk1.8 、tomcat8.5遇到的坑及解决方案
在将spring3.x 升级为4.3.x,jdk1.7 tomcat7升级到jdk1.8.tomcat8.5过程中,碰到了很多问题,也学习到了很多东西,现将这些问题分享出来,方便大家后续遇到同样问题时 ...
- 项目在低版本浏览器下不兼容?友情提示客户升级浏览器(以下只针对IE浏览器)
(function (window) { var win = window, sys = {}, ua = navigator.userAgent.toLowerCase(); (/msie\s+(\ ...
