[NOI2002]荒岛野人（exgcd，枚举）

题目描述

克里特岛以野人群居而著称。岛上有排列成环行的M个山洞。这些山洞顺时针编号为1,2,…,M。岛上住着N个野人，一开始依次住在山洞C1,C2,…,CN中，以后每年，第i个野人会沿顺时针向前走Pi个洞住下来。

每个野人i有一个寿命值Li，即生存的年数。

下面四幅图描述了一个有6个山洞，住有三个野人的岛上前四年的情况。三个野人初始的洞穴编号依次为1，2，3；每年要走过的洞穴数依次为3，7，2；寿命值依次为4，3，1。

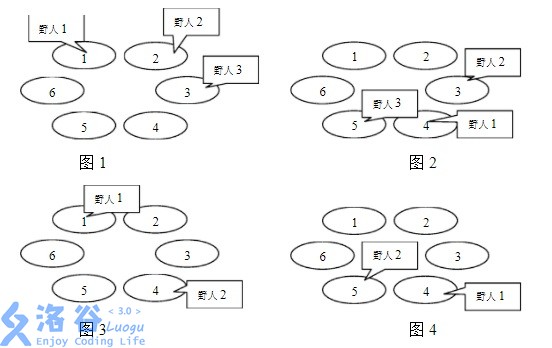
奇怪的是，虽然野人有很多，但没有任何两个野人在有生之年处在同一个山洞中，使得小岛一直保持和平与宁静，这让科学家们很是惊奇。他们想知道，至少有多少个山洞，才能维持岛上的和平呢？

输入输出格式

输入格式：

第1行为一个整数N(1<=N<=15)，即野人的数目。

第2行到第N+1每行为三个整数Ci, Pi, Li (1<=Ci,Pi<=100, 0<=Li<=106 )，表示每个野人所住的初始洞穴编号，每年走过的洞穴数及寿命值。

输出格式：

仅包含一个数M，即最少可能的山洞数。输入数据保证有解，且M不大于10^6。

思路：

既然要求每两个野人永远不能碰面的最少山洞数，我们不妨先看一下数据范围

已知洞穴数小于1e6，那么我们就可以枚举洞穴数量，然后判定是否成立

怎么判定呢？

我们现在已经枚举出了洞穴的数量，然后我们就知道了模数的大小，

就可以利用exgcd两两验证
比如说验证i与j两个位置

则两个野人相遇时，应满足：
yearly[i]*x+start[i]≡start[j]+yearly[j]*x （mod p）

转化一下就是exgcd的形式

验证即可

代码：

#include<iostream>
#include<cstdio>
#include<cmath>
#define rii register int i
#define rij register int j
using namespace std;
int yearly[],start[],life[],x,y,n,ans,maxn;
int gcd(int a,int b)
{
    if(b!=)
    {
        return gcd(b,a%b);
    }
    else
    {
        return a;
    }
}
void exgcd(int ltt,int lzn)
{
    if (lzn!=)
    {
        exgcd(lzn,ltt%lzn);
        int kkk=x;
        x=y;
        y=kkk-ltt/lzn*y;
    }
    else
    {
        x=;
        y=;
    }
}
int check()
{
    for(rii=;i<=n-;i++)
    {
        for(rij=i+;j<=n;j++)
        {
            int kkk=start[i]-start[j];
            int ltt=ans;
            int lzn=yearly[j]-yearly[i];
            int qwq=gcd(kkk,ltt);
            if(lzn%qwq!=)
            {
                continue;
            }
            exgcd(kkk,ltt);
            ltt=abs(ltt/qwq);
            x=(x/qwq*lzn%ltt+ltt)%ltt;
            if(x==)
            {
                x+=ltt;
            }
            if(x<=min(life[i],life[j]))
            {
                return ;
            }
        }
    }
    return ;
}
int main()
{
    scanf("%d",&n);
    for(rii=;i<=n;i++)
    {
        scanf("%d%d%d",&yearly[i],&start[i],&life[i]);
        maxn=max(yearly[i],maxn);
    }
    ans=maxn;
    while(check()!=)
    {
        ans++;
    }
    printf("%d",ans);
}