ode45求解微分方程（MATLAB）

首先介绍一下ode45的格式：

[t,y] = ode45(odefun,tspan,y0)

[t,y] = ode45(odefun,tspan,y0,options)

[t,y,te,ye,ie] = ode45(odefun,tspan,y0,options)

sol = ode45(___)

这里介绍一阶微分方程：

[自变量，因变量] = ode45(方程，范围，初值);

举个栗子：

首先创建一个func2.m函数存放方程表达式

function Biubiu = func2(h, t)
g = 9.8;
Biubiu = (10000*pi/sqrt(2*g))*(h.^(3/2) - 2*(h.^(1/2)));
end

　　

接着在MATLAB命令窗口输入：

tspan = [1 0];%函数范围
t_1 = 0;%初值
[h,t] = ode45(@func2, hspan, t_1);
plot(h,t);%绘图

　　

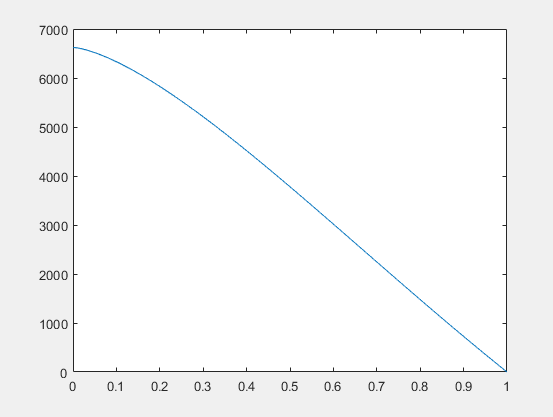
可以丰富一下图像，增加横坐标名，纵坐标名和标题

xlabel('h值')
ylabel('y值')
title('一阶微分方程')

　　

相关资料访问：https://ww2.mathworks.cn/help/matlab/ref/ode45.html?s_tid=doc_ta