洛谷 P4001 [ICPC-Beijing 2006]狼抓兔子

题目描述

现在小朋友们最喜欢的"喜羊羊与灰太狼",话说灰太狼抓羊不到，但抓兔子还是比较在行的，而且现在的兔子还比较笨，它们只有两个窝，现在你做为狼王，面对下面这样一个网格的地形：

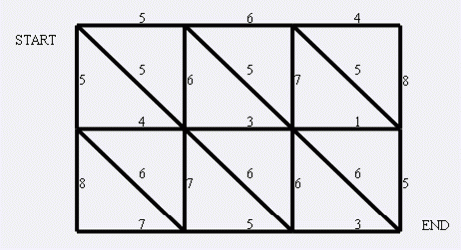
左上角点为(1,1),右下角点为(N,M)(上图中N=3,M=4).有以下三种类型的道路

1:(x,y)<==>(x+1,y)

2:(x,y)<==>(x,y+1)

3:(x,y)<==>(x+1,y+1)

道路上的权值表示这条路上最多能够通过的兔子数，道路是无向的. 左上角和右下角为兔子的两个窝，开始时所有的兔子都聚集在左上角(1,1)的窝里，现在它们要跑到右下角(N,M)的窝中去，狼王开始伏击这些兔子.当然为了保险起见，如果一条道路上最多通过的兔子数为K，狼王需要安排同样数量的K只狼，才能完全封锁这条道路，你需要帮助狼王安排一个伏击方案，使得在将兔子一网打尽的前提下，参与的狼的数量要最小。因为狼还要去找喜羊羊麻烦。

输入输出格式

输入格式：

第一行为N,M.表示网格的大小，N,M均小于等于1000.

接下来分三部分

第一部分共N行，每行M-1个数，表示横向道路的权值.

第二部分共N-1行，每行M个数，表示纵向道路的权值.

第三部分共N-1行，每行M-1个数，表示斜向道路的权值.

输出格式：

输出一个整数，表示参与伏击的狼的最小数量.

输入输出样例

输入样例#1：

3 4
5 6 4
4 3 1
7 5 3
5 6 7 8
8 7 6 5
5 5 5
6 6 6

输出样例#1：

14

思路：按照题目中所说的，见横向，纵向和沿对角线的边，题目显然是要我们求最小割，直接跑dinic求最大流就可以了。

代码：

#include<cstdio>
#include<cstring>
#include<cctype>
#include<queue>
#define maxn 2000007
#define inf 0x3f3f3f3f
using namespace std;
int n,m,S=1,T,head[maxn],num=1,d[maxn];
inline int qread() {
  char c=getchar();int num=0,f=1;
  for(;!isdigit(c);c=getchar()) if(c=='-') f=-1;
  for(;isdigit(c);c=getchar()) num=num*10+c-'0';
  return num*f;
}
struct node {
  int v,w,nxt;
}e[6000007];
inline void ct(int u, int v, int w) {
  e[++num].v=v;
  e[num].w=w;
  e[num].nxt=head[u];
  head[u]=num;
}
inline bool bfs() {
  memset(d,-1,sizeof(d));
  queue<int>q;
  q.push(S),d[S]=0;
  while(!q.empty()) {
  	int u=q.front();
  	q.pop();
  	for(int i=head[u];i;i=e[i].nxt) {
  	  int v=e[i].v;
  	  if(e[i].w&&d[v]==-1) {
  	    d[v]=d[u]+1;
		q.push(v);
	  }
	}
  }
  return d[T]!=-1;
}
int dfs(int u, int f) {
  if(u==T) return f;
  int rest=f;
  for(int i=head[u];i;i=e[i].nxt) {
  	int v=e[i].v;
  	if(d[v]==d[u]+1&&e[i].w&&rest) {
  	  int t=dfs(v,min(e[i].w,rest));
	  if(!t) d[v]=0;
	  e[i].w-=t;
	  e[i^1].w+=t;
	  rest-=t;
	}
  }
  return f-rest;
}
inline int dinic() {
  int ans=0;
  while(bfs()) ans+=dfs(S,inf);
  return ans;
}
int main() {
  n=qread(),m=qread();
  T=n*m;
  for(int i=1;i<=n;++i) {
  	int tmp=(i-1)*m;
  	for(int j=1,x;j<m;++j) {
  	  x=qread();
	  ct(tmp+j,tmp+j+1,x),ct(tmp+1+j,tmp+j,x);
	}
  }
  for(int i=1;i<n;++i) {
  	int tmp=(i-1)*m;
  	for(int j=1,x;j<=m;++j) {
  	  x=qread();
	  ct(tmp+j,tmp+j+m,x),ct(tmp+j+m,tmp+j,x);
	}
  }
  for(int i=1;i<n;++i) {
	int tmp=(i-1)*m;
	for(int j=1,x;j<m;++j) {
	  x=qread();
	  ct(tmp+j,tmp+m+j+1,x),ct(tmp+m+1+j,tmp+j,x);
	}
  }
  printf("%d\n",dinic());
  return 0;
}