BZOJ3144/LG3227 「HNOI2013」切糕 最小割离散变量模型

问题描述

BZOJ3144

LG3227

还想粘下样例

输入：

2 2 2
1
6 1
6 1
2 6
2 6

输出：

6

---

题解

关于离散变量模型，我不想再抄一遍，所以：

对于样例，可以建立出这样的图

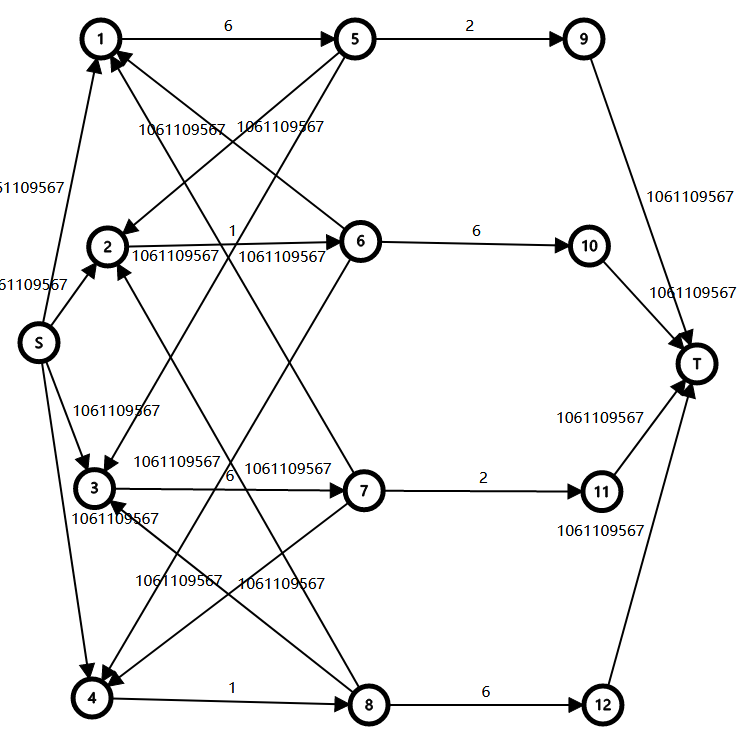
这是一个最小割模型，哪条边满流就代表在这个位置选择了哪个值。

网络流的主要思想就是通过点互化，将限制条件在边上体现出来。

所以比 \([1,r]\) 要再多建立一个点，但是最后增加的一层不能建立横向边 。

---

\(\mathrm{Code}\)

#include<bits/stdc++.h>
using namespace std;

const int maxn=42;
const int INF=0x3f3f3f3f;

int p,q,r,D;
int v[maxn][maxn][maxn];

int Head[maxn*maxn*maxn*2],Next[maxn*maxn*maxn*10],to[maxn*maxn*maxn*10],w[maxn*maxn*maxn*10],tot=1;

int S,T;
void add(int x,int y,int z){
//	if(x==4&&y==S) puts("Warning!");
//	if(x==S&&y==4) puts("Warning!");
	to[++tot]=y,Next[tot]=Head[x],Head[x]=tot,w[tot]=z;
}

int id(int x,int y,int z){
	return (z-1)*p*q+(x-1)*q+y;
}

void Init(void){
	scanf("%d%d%d%d",&p,&q,&r,&D);
	for(int i=1;i<=r;i++){
		for(int j=1;j<=p;j++){
			for(int k=1;k<=q;k++){
				scanf("%d",&v[j][k][i]);
			}
		}
	}
}

int dx[4]={0,0,1,-1};
int dy[4]={1,-1,0,0};

bool check(int x,int y,int z){
	return ((x>=1&&x<=p)&&(y>=1&&y<=q)&&(z>=1&&z<=r));
}

void Graph_build(void){
	S=p*q*(r+1)+2,T=S+1;
	for(int i=1;i<=p;i++){
		for(int j=1;j<=q;j++){
			add(S,id(i,j,1),INF);add(id(i,j,1),S,0);
			for(int k=1;k<=r;k++){
				add(id(i,j,k),id(i,j,k+1),v[i][j][k]);
				add(id(i,j,k+1),id(i,j,k),0);
//				add(id(i,j,k),id(i,j,k-1),v[i][j][k-1]);
//				add(id(i,j,k-1),id(i,j,k),0);
			}
			add(id(i,j,r+1),T,INF);add(T,id(i,j,r+1),0);
		}
	}
	for(int i=1;i<=p;i++){
		for(int j=1;j<=q;j++){
			for(int e=0;e<4;e++){
				int mx=i+dx[e],my=j+dy[e];
				if(mx<1||mx>p||my<1||my>q) continue;
				for(int h=D+1;h<=r;h++){
					add(id(i,j,h),id(mx,my,h-D),INF);
					add(id(mx,my,h-D),id(i,j,h),0);
				}
			}
		}
	}
}

int ans;
int d[maxn];

bool bfs(void){
	memset(d,0,sizeof(d));
	queue<int>q;q.push(S);d[S]=1;
	while(q.size()){
		int x=q.front();q.pop();
		for(int i=Head[x];i;i=Next[i]){
			int y=to[i];
			if(d[y]||!w[i]) continue;
			d[y]=d[x]+1;q.push(y);
			if(y==T) return true;
		}
	}
	return false;
}

int dfs(int x,int flow){
	if(x==T) return flow;
	int rest=flow;
	for(int i=Head[x];i&&rest;i=Next[i]){
		int y=to[i];
		if(d[y]!=d[x]+1||!w[i]) continue;
		int k=dfs(y,min(rest,w[i]));
		if(!k) d[y]=0;
		else w[i]-=k,w[i^1]+=k,rest-=k;
	}
	return flow-rest;
}

void Dinic(void){
	int t;
	while(bfs()){
		while(t=dfs(S,INF)) ans+=t;
	}
}

void Dbug(){
	for(int i=2;i<=tot;i+=2){
		printf("%d %d %d\n",to[i^1],to[i],w[i]);
	}
}

//#define debug

void Work(void){
	Graph_build();

	#ifdef debug
		Dbug();
		printf("S:%d T:%d\n",S,T);
	#endif
	Dinic();
	printf("%d\n",ans);
}

int main(){
	Init();
	Work();
	return 0;
}