算法导论-求(Fibonacci)斐波那契数列算法对比

目录

1、斐波那契数列（Fibonacci）介绍

2、朴素递归算法（Naive recursive algorithm）

3、朴素递归平方算法（Naive recursive squaring）

4 、自底向上算法（Bottom-up）

5、 递归平方算法（Recursive squaring）

6、完整代码（c++）

7、参考资料

内容

1、斐波那契数列（Fibonacci）介绍

Fibonacci数列应该也算是耳熟能详，它的递归定义如上图所示。

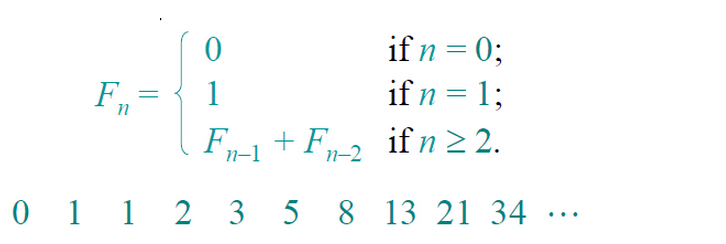
下面2-6分别说明求取Fibonacci数列的4种方法

2、朴素递归算法（Naive recursive algorithm）

在很多C语言教科书中讲到递归函数的时候，都会用Fibonacci作为例子。因此很多程序员对这道题的递归解法非常熟悉，看到题目就能写出如下的递归求解的代码

  unsigned long long Fibonacci_naive_reu(int n)//朴素递归算法
 {
     int result[] = {,};
     if (n<)       //退出条件
        return result[n];

     return (Fibonacci_naive_reu(n-)+ Fibonacci_naive_reu(n-));//递归调用
 }

其实这种想法很好，但该算法运行时间令人无法忍受，当计算n=50时,用时1200多秒

分析：该算法的时间复杂度T(n)=Θ(∂ⁿ),其中，∂ = (1 + 5^½) / 2，即黄金分割比率。可知，∂>1,随着n增加，时间指数快速增加，所以，平时很少采用！

3、朴素递归平方算法（Naive recursive squaring）

这个算法主要根据斐波那契数列的一条数学性质而来。该性质表明，斐波那契数列F(n)即为φ^n / 5^½向下取整。这样，问题的求解于是变成了一个求x的n次方的问题，在之前的文章里有讲解，链接请进。 所以算法的效率为Θ(lgn)。但是这个方法是不太靠谱的，主要是当n比较大时，由于硬件的限制计算机中的浮点运算得到的结果与真实值就产生误差了。实用价值也不大，只能用做理论分析。

4 、自底向上算法（Bottom-up）

考虑到2中的简单递归算法，为了求解F(n)，需要同时递归求解F(n - 1)和F(n - 2)，显然这样就做了大量的重复工作。采用自底向上的算法即可避免这样的冗余。要计算F(n)，则依次计算F0，F1，F2。。。Fn，这时计算Fn只需要利用前两个结果即可，这样算法效率提高到了Θ(n)。n=50时，小于1毫秒。实用价值高。

算法代码：

  /************************************************************************/
  /*                         自底向上算法                                         */
  //  时间复杂度T(n)=o(n)
  /************************************************************************/
 unsigned long long Fibonacci_bottom_up(int n)//自底向上算法
 {
     int result[] = {, };
     if(n < )
         return result[n];

     unsigned long long  fibNMinusN_1 = ;
     unsigned long long  fibNMinusN_2 = ;
     unsigned long long  fibN = ;
     for(int i = ; i <= n; ++ i)   //从底到上逐次计算出数列值
     {
         fibN = fibNMinusN_1 + fibNMinusN_2;

         fibNMinusN_2 = fibNMinusN_1;
         fibNMinusN_1 = fibN;
     }

     return fibN;//返回数组值
 }

5、 递归平方算法（Recursive squaring）

上面的算法已经能达到Θ(n)线性效率，然而下面的这个算法能使效率达到T(n) = Θ(lgn)。该算法是基于一个定理，定理以及证明过程如下图所示。这样，问题的求解即成为了矩阵的乘方问题，算法效率于是提高到了Θ(lgn)。

矩阵求幂方法同常数求幂方法，采用分治思想，可参见常数求幂方法，下面是矩阵求幂实现代码：

 /************************************************************************/
 /*  下面矩阵的n次幂，结果保存在      Result[2][2]                   */
 //   矩阵的n次幂，采用分治法，与x的n 次方算法一致，时间复杂度T(n)=o(logn)
 //    1    1
 //    1    0
 /************************************************************************/
 void Matrix_power(int n,unsigned long long Result[][])//求矩阵幂
 {
     unsigned long long AResult[][];
     unsigned long long zResult1[][];
     unsigned long long zResult2[][];

     AResult[][]=;AResult[][]=;AResult[][]=;AResult[][]=;
     if (==n)
     {
         Result[][]=;Result[][]=;Result[][]=;Result[][]=;
     }
     else if (n%==)
     {
         Matrix_power(n/,zResult1);
         MUL(zResult1,zResult1,Result);
     }
     else if (n% == )
     {
         Matrix_power((n-)/,zResult1);
         MUL(zResult1,zResult1,zResult2);
         MUL(zResult2,AResult,Result);
     }
 }

其中，两个矩阵相乘代码实现如下：

 /************************************************************************/
 /* 两个 矩阵相乘  、结果矩阵保存在 MatrixResult[2][2]中       */
 /************************************************************************/
 void MUL( unsigned long long MatrixA[][],unsigned long long MatrixB[][], unsigned long long MatrixResult[][] )//矩阵相乘
 {
     for (int i=;i< ;i++)
     {
         for (int j=;j< ;j++)
         {
             MatrixResult[i][j]=;
             for (int k=;k< ;k++)
             {
                 MatrixResult[i][j]=MatrixResult[i][j]+MatrixA[i][k]*MatrixB[k][j];
             }
         }
     }
 }

6、完整代码（c++）

Fibonacci.h   其中递归平方法（矩阵求幂法）有两种实现，一种是我自己编码实现，另外是网上copy的代码。

 #ifndef FIBONACCI_HH
 #define FIBONACCI_HH
 struct Matrix2By2
 {
     Matrix2By2
         (
         unsigned long long m00 = ,
         unsigned long long m01 = ,
         unsigned long long m10 = ,
         unsigned long long m11 =
         )
         :m_00(m00), m_01(m01), m_10(m10), m_11(m11)
     {
     }

     unsigned long long m_00;
     unsigned long long m_01;
     unsigned long long m_10;
     unsigned long long m_11;
 };
 class Fibonacci
 {
 public:
     unsigned long long Fibonacci_naive_reu(int n);//朴素递归算法
     unsigned long long Fibonacci_bottom_up(int n);//自底向上算法
     unsigned long long Fibonacci_recur_squar(int n);//递归平方算法
     void MUL( unsigned long long MatrixA[][],unsigned long long MatrixB[][], unsigned long long MatrixResult[][] );
     void  Matrix_power(int n,unsigned long long result[][]);

     Matrix2By2 MatrixMultiply(const Matrix2By2& matrix1, const Matrix2By2& matrix2);
     Matrix2By2 MatrixPower(unsigned int n);
     unsigned long long Fibonacci_Solution3(unsigned int n);

 };

  unsigned long long Fibonacci::Fibonacci_naive_reu(int n)//朴素递归算法
 {
     int result[] = {,};
     if (n<)       //退出条件
        return result[n];

     return (Fibonacci_naive_reu(n-)+ Fibonacci_naive_reu(n-));//递归调用
 }
  /************************************************************************/
  /*                         自底向上算法                                         */
  //  时间复杂度T(n)=o(n)
  /************************************************************************/
 unsigned long long Fibonacci::Fibonacci_bottom_up(int n)//自底向上算法
 {
     int result[] = {, };
     if(n < )
         return result[n];

     unsigned long long  fibNMinusN_1 = ;
     unsigned long long  fibNMinusN_2 = ;
     unsigned long long  fibN = ;
     for(int i = ; i <= n; ++ i)   //从底到上逐次计算出数列值
     {
         fibN = fibNMinusN_1 + fibNMinusN_2;

         fibNMinusN_2 = fibNMinusN_1;
         fibNMinusN_1 = fibN;
     }

     return fibN;//返回数组值
 }
 /************************************************************************/
 /* 两个 矩阵相乘  、结果矩阵保存在 MatrixResult[2][2]中       */
 /************************************************************************/
 void Fibonacci::MUL( unsigned long long MatrixA[][],unsigned long long MatrixB[][], unsigned long long MatrixResult[][] )//矩阵相乘
 {
     for (int i=;i< ;i++)
     {
         for (int j=;j< ;j++)
         {
             MatrixResult[i][j]=;
             for (int k=;k< ;k++)
             {
                 MatrixResult[i][j]=MatrixResult[i][j]+MatrixA[i][k]*MatrixB[k][j];
             }
         }
     }
 }
 /************************************************************************/
 /*  下面矩阵的n次幂，结果保存在      Result[2][2]                   */
 //   矩阵的n次幂，采用分治法，与x的n 次方算法一致，时间复杂度T(n)=o(logn)
 //    1    1
 //    1    0
 /************************************************************************/
 void Fibonacci::Matrix_power(int n,unsigned long long Result[][])//求矩阵幂
 {
     unsigned long long AResult[][];
     unsigned long long zResult1[][];
     unsigned long long zResult2[][];

     AResult[][]=;AResult[][]=;AResult[][]=;AResult[][]=;
     if (==n)
     {
         Result[][]=;Result[][]=;Result[][]=;Result[][]=;
     }
     else if (n%==)
     {
         Matrix_power(n/,zResult1);
         MUL(zResult1,zResult1,Result);
     }
     else if (n% == )
     {
         Matrix_power((n-)/,zResult1);
         MUL(zResult1,zResult1,zResult2);
         MUL(zResult2,AResult,Result);
     }
 }
 unsigned long long Fibonacci::Fibonacci_recur_squar(int n)//递归平方算法
 {
     unsigned long long fib_result[][];
     int result[] = {, };
     if(n < )
         return result[n];
     Matrix_power(n,fib_result);
     return fib_result[][];
 }

 /************************************************************************/
 /*     下面是网上copy的递归平方算法的代码                          */
 /************************************************************************/
 ///////////////////////////////////////////////////////////////////////
 // Multiply two matrices
 // Input: matrix1 - the first matrix
 //        matrix2 - the second matrix
 //Output: the production of two matrices
 ///////////////////////////////////////////////////////////////////////
 Matrix2By2 Fibonacci::MatrixMultiply
     (
     const Matrix2By2& matrix1,
     const Matrix2By2& matrix2
     )
 {
     return Matrix2By2(
         matrix1.m_00 * matrix2.m_00 + matrix1.m_01 * matrix2.m_10,
         matrix1.m_00 * matrix2.m_01 + matrix1.m_01 * matrix2.m_11,
         matrix1.m_10 * matrix2.m_00 + matrix1.m_11 * matrix2.m_10,
         matrix1.m_10 * matrix2.m_01 + matrix1.m_11 * matrix2.m_11);
 }

 ///////////////////////////////////////////////////////////////////////
 // The nth power of matrix
 // 1  1
 // 1  0
 ///////////////////////////////////////////////////////////////////////
 Matrix2By2 Fibonacci::MatrixPower(unsigned int n)
 {
     Matrix2By2 matrix;
     if(n == )
     {
         matrix = Matrix2By2(, , , );
     }
     else if(n %  == )
     {
         matrix = MatrixPower(n / );
         matrix = MatrixMultiply(matrix, matrix);
     }
     else if(n %  == )
     {
         matrix = MatrixPower((n - ) / );
         matrix = MatrixMultiply(matrix, matrix);
         matrix = MatrixMultiply(matrix, Matrix2By2(, , , ));
     }

     return matrix;
 }
 ///////////////////////////////////////////////////////////////////////
 // Calculate the nth item of Fibonacci Series using devide and conquer
 ///////////////////////////////////////////////////////////////////////
 unsigned long long Fibonacci::Fibonacci_Solution3(unsigned int n)
 {
     int result[] = {, };
     if(n < )
         return result[n];

     Matrix2By2 PowerNMinus2 = MatrixPower(n - );
     return PowerNMinus2.m_00;
 }
 #endif

Fibonacci.h

Fibonacci.cpp (主函数)

 #include <iostream>
 #include <vector>
 #include <ctime>
 using namespace std;
 #include "Fibonacci.h"

 int main()
 {
     Fibonacci fib;
     clock_t startTime_For_Fibonacci_naive_reu ;
     clock_t endTime_For_Fibonacci_naive_reu ;
     clock_t startTime_For_Fibonacci_bottom_up ;
     clock_t endTime_For_Fibonacci_bottom_up ;
     clock_t startTime_For_Fibonacci_recur_squar1 ;
     clock_t endTime_For_Fibonacci_recur_squar1 ;
     clock_t startTime_For_Fibonacci_recur_squar2 ;
     clock_t endTime_For_Fibonacci_recur_squar2 ;

     startTime_For_Fibonacci_naive_reu=clock();
     cout<<fib.Fibonacci_naive_reu()<<endl;//朴素递归算法
     endTime_For_Fibonacci_naive_reu=clock();

     startTime_For_Fibonacci_bottom_up=clock();
     cout<<fib.Fibonacci_bottom_up()<<endl;//自底向上算法
     endTime_For_Fibonacci_bottom_up=clock();

     startTime_For_Fibonacci_recur_squar1=clock();
     cout<<fib.Fibonacci_recur_squar()<<endl;//我自己编写的递归平方算法
     endTime_For_Fibonacci_recur_squar1=clock();

     startTime_For_Fibonacci_recur_squar2=clock();
     cout<<fib.Fibonacci_Solution3()<<endl;//网上copy的递归平方算法
     endTime_For_Fibonacci_recur_squar2=clock();

     cout<<"朴素递归算法用时： "<<(endTime_For_Fibonacci_naive_reu-startTime_For_Fibonacci_naive_reu)/(1.0*CLOCKS_PER_SEC)<<"秒"<<endl;
     cout<<"自底向上算法用时： "<<(endTime_For_Fibonacci_bottom_up-startTime_For_Fibonacci_bottom_up)/(1.0*CLOCKS_PER_SEC)<<"秒"<<endl;
     cout<<"我自己编写的递归平方算法用时： "<<(endTime_For_Fibonacci_recur_squar1-startTime_For_Fibonacci_recur_squar1)/(1.0*CLOCKS_PER_SEC)<<"秒"<<endl;
     cout<<"网上copy的递归平方算法用时： "<<(endTime_For_Fibonacci_recur_squar2-startTime_For_Fibonacci_recur_squar2)/(1.0*CLOCKS_PER_SEC)<<"秒"<<endl;
     system("Pause");
     return ;
 }

输出：

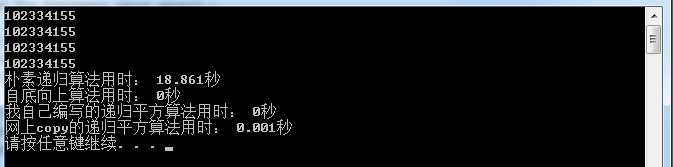
结：朴素递归算法用时太多，实用价值不大，自底向上算法效率为线性，较高，平时用较多，递归平方算法效率为对数级，且编程可实现，实用价值很大。并且经过测试，当n值变很大后，递归平方算法效率明显高于自底向上算法效率。

7、参考资料

【1】http://zhedahht.blog.163.com/blog/static/25411174200722991933440/

【2】http://blog.csdn.net/xyd0512/article/details/8220506