最小生成树的kruskal、prim算法
kruskal算法和prim算法
都说 kruskal是加边法,prim是加点法
这篇解释也不错:这篇
1、kruskal算法
因为是加边法,所以这个方法比较合适稀疏图。要码这个需要先懂并查集。因为我不会画好看的图,所以看不懂的话推荐下面博客的说明。这里是下面。
步骤:
1、把每个点都看成一棵树,那么你就会得到一片森林。。。
2、把每棵树之间的距离从小到大排序,即把边排序
3、从小到大取边,把不在同一棵树的点连通到同一棵树上。。。最后你会得到一棵树,就是最小生成树
我去盗图。。。这里的图
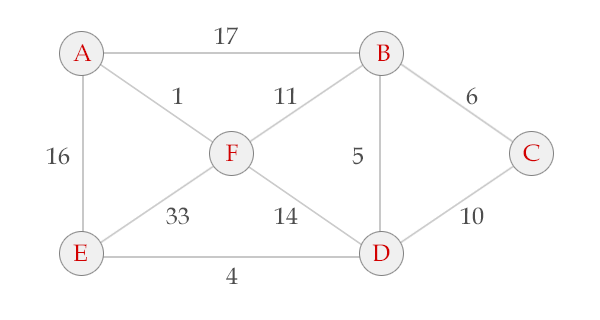
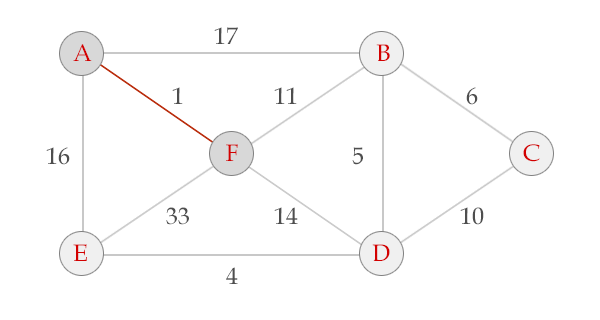
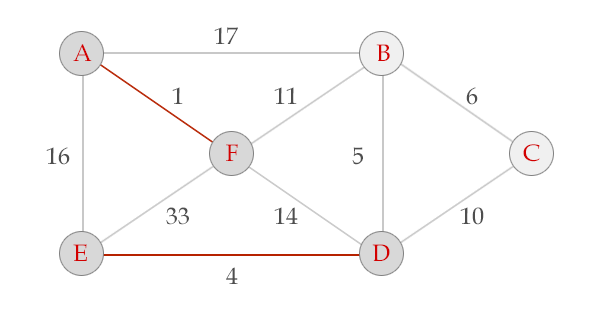
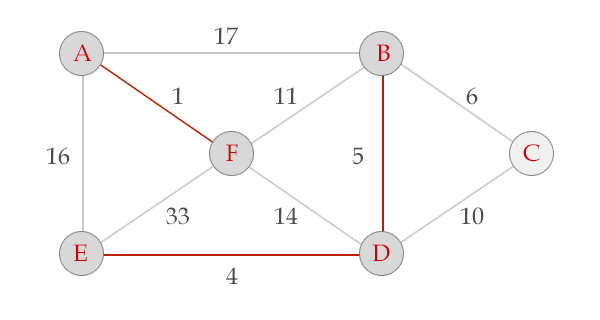
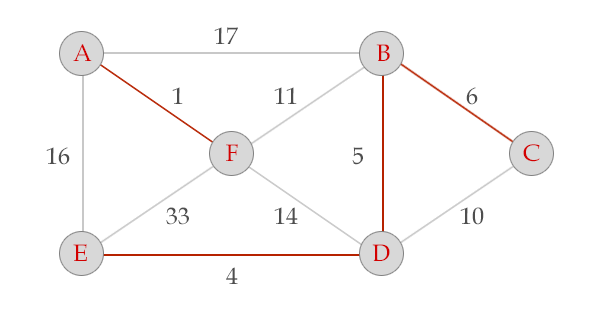
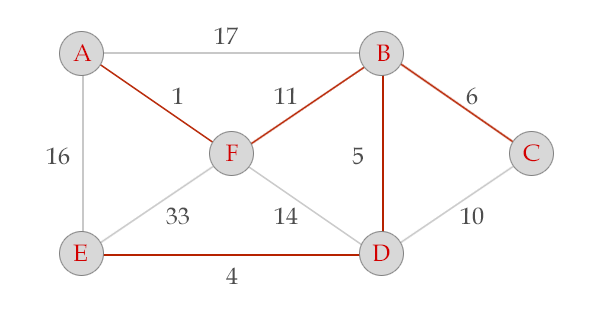
给个模板题吧。。HDU1233
#include <iostream>
#include <cstdio>
#include <string>
#include <cstring>
#include <cmath>
#include <sstream>
#include <algorithm>
#include <set>
#include <map>
#include <vector>
#include <queue>
#include <iomanip>
#include <stack> using namespace std; typedef long long LL;
const int INF = 0x3f3f3f3f;
const int MAXN = ;
const int MOD = 1e9 + ; #define MemI(x) memset(x, -1, sizeof(x))
#define Mem0(x) memset(x, 0, sizeof(x))
#define MemM(x) memset(x, 0x3f, sizeof(x)) struct Edge
{
int u, v, w;
bool operator < (const Edge &a) const
{
return w < a.w;
}
}edge[MAXN];
int n, ans, fa[]; //找父节点并压缩路径,这是并查集的知识
int Get_f(int x)
{
if(fa[x] == x)
return x;
return fa[x] = Get_f(fa[x]);
} void Kruskal()
{
//初始化
for(int i = ;i <= n;++i)
fa[i] = i;
sort(edge, edge + (n - ) * n / );
ans = ; int x, y, cnt = ;
for(int i = ;i < n * (n - ) / ;++i)
{
x = Get_f(edge[i].u), y = Get_f(edge[i].v);
//加边
if(x != y)
{
ans += edge[i].w;
fa[x] = y;
cnt++;
}
//加入所有点了
if(cnt >= n)
break;
}
printf("%d\n", ans);
} int main()
{
while(scanf("%d", &n) != EOF && n)
{
for(int i = ;i < n * (n - ) / ;++i)
scanf("%d%d%d", &edge[i].u, &edge[i].v, &edge[i].w);
Kruskal();
}
return ;
}
2、Prim算法
这算法写起来跟最短路的 Dijkstra算法很像。来复习一下 Dijkstra算法,先找出距离源点最短的点(这里是找出离一个点最近的路),然后把这个点与。源点连接(这里是连接这两个点),之后再更新最短路(更新到各个点的最短的边,这里代码有点不同)。。。就没有哈哈哈哈。。。直接上上面那道模板题代码吧。。。。。
#include <iostream>
#include <cstdio>
#include <string>
#include <cstring>
#include <cmath>
#include <sstream>
#include <algorithm>
#include <set>
#include <map>
#include <vector>
#include <queue>
#include <iomanip>
#include <stack> using namespace std; typedef long long LL;
const int INF = 0x3f3f3f3f;
const int MAXN = ;
const int MOD = 1e9 + ; #define MemI(x) memset(x, -1, sizeof(x))
#define Mem0(x) memset(x, 0, sizeof(x))
#define MemM(x) memset(x, 0x3f, sizeof(x)) int mp[MAXN][MAXN], dis[MAXN], n, ans;
bool vis[MAXN]; void Prim(int s)
{
Mem0(vis);
int i, j;
for(i = ;i <= n;++i)
dis[i] = mp[s][i];
dis[s] = ;
int v, w;
vis[s] = true;
for(i = ;i < n;++i)
{
w = INF;
for(j = ;j <= n;++j)
{
if(!vis[j] && dis[j] < w)
{
w = dis[j];
v = j;
}
}
vis[v] = true;
ans += w;
for(j = ;j <= n;++j)
if(!vis[j] && dis[j] > mp[v][j])//这里不同
dis[j] = mp[v][j];
}
printf("%d\n", ans);
} int main()
{
int a, b, c;
while(scanf("%d", &n) != EOF && n)
{
MemM(mp);
ans = ;
for(int i = ;i < n * (n - ) / ;++i)
{
scanf("%d%d%d", &a, &b, &c);
mp[a][b] = mp[b][a] = c;
}
Prim();
}
return ;
}
3、 STL与kruskal(理论上 Prim算法应该能用优先队列简化找最短路径的操作,就。。不码这个了)
用map存边,简化排序操作。。。先是模板题练练手,可是跑出来时间慢了十几毫秒
#include <iostream>
#include <cstdio>
#include <string>
#include <cstring>
#include <cmath>
#include <sstream>
#include <algorithm>
#include <set>
#include <map>
#include <vector>
#include <queue>
#include <iomanip>
#include <stack> using namespace std; typedef long long LL;
const int INF = 0x3f3f3f3f;
const int MAXN = ;
const int MOD = 1e9 + ; #define MemI(x) memset(x, -1, sizeof(x))
#define Mem0(x) memset(x, 0, sizeof(x))
#define MemM(x) memset(x, 0x3f, sizeof(x)) int ans, n, fa[MAXN];
int Get_F(int x)
{
if(fa[x] == x)
return x;
return fa[x] = Get_F(fa[x]);
} int main()
{
while(scanf("%d", &n) != EOF && n)
{
ans = ;
multimap<int, pair<int, int> > mp;
for(int i = ;i <= n;++i)
fa[i] = i;
int a, b, c;
for(int i = ;i < n * (n - ) / ;++i)
{
scanf("%d%d%d", &a, &b, &c);
mp.insert(make_pair(c, make_pair(a, b)));
}
multimap<int, pair<int, int> > :: iterator it;
int x, y;
for(it = mp.begin();it != mp.end();++it)
{
x = Get_F((*it).second.first), y = Get_F((*it).second.second);
if(x != y)
{
fa[x] = y;
ans += (*it).first;
}
}
printf("%d\n", ans);
}
return ;
}
再给多一道题 UVALive - 6437,先用Prim写一下,感觉Prim比较容易理解,然后再用 kruskal写个简单版的。
Prim思路:。。。。下面注释吧。
#include <iostream>
#include <cstdio>
#include <string>
#include <cstring>
#include <cmath>
#include <sstream>
#include <algorithm>
#include <set>
#include <map>
#include <vector>
#include <queue>
#include <iomanip>
#include <stack> using namespace std; typedef long long LL;
const int INF = 0x3f3f3f3f;
const int MAXN = ;
const int MOD = 1e9 + ; #define MemI(x) memset(x, -1, sizeof(x))
#define Mem0(x) memset(x, 0, sizeof(x))
#define MemM(x) memset(x, 0x3f, sizeof(x)) //点数 n,边数 m ,发电站数量 num, 图 mp, 发电站 power
int ans, n, m, num, vis[MAXN], dis[MAXN], mp[MAXN][MAXN];
int power[MAXN];
int Prim()
{
int i, j, k;
// 各个城镇到各个发电站的最短距离
MemM(dis);
for(i = ;i <= n;++i)
for(j = ;j < num;++j)
dis[i] = min(dis[i], mp[i][power[j]]);
int w, v;
// 还要对 n - num 个点找最短路
for(i = ;i < n - num;++i)
{
w = INF;
for(j = ;j <= n;++j)
if(!vis[j] && dis[j] < w)
{
w = dis[j];
v = j;
}
vis[v] = true;
ans += w;
// 这里可以理解为城镇新建了发电站,就看其他城镇到这个新发电站的距离
for(j = ;j <= n;++j)
if(!vis[j] && dis[j] > mp[v][j])
dis[j] = mp[v][j];
}
return ans;
} int main()
{
int T;
scanf("%d", &T);
for(int cas = ;cas <= T;++cas)
{
MemM(mp);
Mem0(vis);
ans = ;
scanf("%d%d%d", &n, &m, &num);
for(int i = ;i <= n;++i)
mp[i][i] = ;
int a, b, c;
for(int i = ;i < num;++i)
{
scanf("%d", &power[i]);
vis[power[i]] = true;//这里先处理发电站比较方便
}
for(int i = ;i < m;++i)
{
scanf("%d%d%d", &a, &b, &c);
mp[a][b] = mp[b][a] = c;
}
printf("Case #%d: %d\n", cas, Prim());
}
return ;
}
Kruskal。。。这道题把所有发电站都先放到一个集合里,那么最后出来的最小生成树就是答案了。。。。具体点就是把所有发电站的祖先都设为同一个,这样不管连接哪一个发电站都有共同祖先。
慢了30ms左右
#include <iostream>
#include <cstdio>
#include <string>
#include <cstring>
#include <cmath>
#include <sstream>
#include <algorithm>
#include <set>
#include <map>
#include <vector>
#include <queue>
#include <iomanip>
#include <stack> using namespace std; typedef long long LL;
const int INF = 0x3f3f3f3f;
const int MAXN = ;
const int MOD = 1e9 + ; #define MemI(x) memset(x, -1, sizeof(x))
#define Mem0(x) memset(x, 0, sizeof(x))
#define MemM(x) memset(x, 0x3f, sizeof(x)) int ans, n, m, k, fa[MAXN];
int Get_F(int x)
{
if(fa[x] == x)
return x;
return fa[x] = Get_F(fa[x]);
} int main()
{
int T;
scanf("%d", &T);
for(int cas = ;cas <= T;++cas)
{
multimap<int, pair<int, int> > mp;
multimap<int, pair<int, int> > :: iterator it;
ans = ;
scanf("%d%d%d", &n, &m, &k);
for(int i = ;i <= n;++i)
fa[i] = i;
int a, b, c;
//处理发电站
scanf("%d", &a);
for(int i = ;i < k;++i)
{
scanf("%d", &b);
fa[b] = a;
}
for(int i = ;i < m;++i)
{
scanf("%d%d%d", &a, &b, &c);
mp.insert(make_pair(c, make_pair(a, b)));
}
ans = ;
int x, y;
for(it = mp.begin();it != mp.end();++it)
{
x = Get_F((*it).second.first), y = Get_F((*it).second.second);
if(x != y)
{
ans += (*it).first;
fa[x] = y;
}
}
printf("Case #%d: %d\n", cas, ans);
}
return ;
}
最小生成树的kruskal、prim算法的更多相关文章
- 最小生成树(Kruskal+Prim)--模板
最小生成树-----在连通网的所有生成树中,所有边的代价和最小的生成树,称为最小生成树. 应用场景 1.假设以下情景,有一块木板,板上钉上了一些钉子,这些钉子可以由一些细绳连接起来.假设每个钉子可以通 ...
- 数据结构与算法--最小生成树之Prim算法
数据结构与算法--最小生成树之Prim算法 加权图是一种为每条边关联一个权值或称为成本的图模型.所谓生成树,是某图的一棵含有全部n个顶点的无环连通子图,它有n - 1条边.最小生成树(MST)是加权图 ...
- hiho 1097 最小生成树一·Prim算法 (最小生成树)
题目: 时间限制:10000ms 单点时限:1000ms 内存限制:256MB 描述 最近,小Hi很喜欢玩的一款游戏模拟城市开放出了新Mod,在这个Mod中,玩家可以拥有不止一个城市了! 但是,问 ...
- 数据结构之最小生成树Prim算法
普里姆算法介绍 普里姆(Prim)算法,是用来求加权连通图的最小生成树算法 基本思想:对于图G而言,V是所有顶点的集合:现在,设置两个新的集合U和T,其中U用于存放G的最小生成树中的顶点,T存放G的最 ...
- POJ-3026(图上的最小生成树+prim算法+gets函数使用)
Borg Maze POJ-3026 一开始看到这题是没有思路的,看了题解才知道和最小生成树有关系. 题目的意思是每次走到一个A或者S就可以分为多个部分继续进行搜索.这里就可以看出是从该点分出去的不同 ...
- MAT之prim算法
prim算法 边赋以权值的图称为网或带权图,带权图的生成树也是带权的,生成树T各边的权值总和称为该树的权. 最小生成树(MST):权值最小的生成树. 生成树和最小生成树的应用:要连通n个城市需要n-1 ...
- Prim算法(普里姆算法)
描述: 一个连通图的生成树是指一个极小连通子图,它含有图中的全部顶点,但只有足以构成一棵树的 n-1 条边.我们把构造连通网的最小代价生成树成为最小生成树.而Prim算法就是构造最小生成树的一种算法. ...
- 数据结构与算法系列研究七——图、prim算法、dijkstra算法
图.prim算法.dijkstra算法 1. 图的定义 图(Graph)可以简单表示为G=<V, E>,其中V称为顶点(vertex)集合,E称为边(edge)集合.图论中的图(graph ...
- 贪心算法-最小生成树Kruskal算法和Prim算法
Kruskal算法: 不断地选择未被选中的边中权重最轻且不会形成环的一条. 简单的理解: 不停地循环,每一次都寻找两个顶点,这两个顶点不在同一个真子集里,且边上的权值最小. 把找到的这两个顶点联合起来 ...
- 最小生成树--Prim算法,基于优先队列的Prim算法,Kruskal算法,Boruvka算法,“等价类”UnionFind
最小支撑树树--Prim算法,基于优先队列的Prim算法,Kruskal算法,Boruvka算法,“等价类”UnionFind 最小支撑树树 前几节中介绍的算法都是针对无权图的,本节将介绍带权图的最小 ...
随机推荐
- Entity Framework 6.0 Tutorials(8):Custom Code-First Conventions
Custom Code-First Conventions: Code-First has a set of default behaviors for the models that are ref ...
- 【原创】boost::recursive_mutex请小心使用
recursive_mutex会减少死锁几率?恩看上去的确如此,但是事实上呢?我们从BOOST的官方逻辑去理解: recursive_mutex类可多次进入锁,这样在递归时可以避免一次死锁的几率,这是 ...
- HDU 4430 Yukari's Birthday (二分)
题意:有 n 个蜡烛,让你插到蛋糕上,每一层要插 k^i个根,第0层可插可不插,插的层数是r,让 r * k 尽量小,再让 r 尽量小,求r 和 k. 析:首先先列出方程来,一个是不插的一个是插的,比 ...
- MongoDB整理笔记のCapped Collection
1.简单介绍 capped collections 是性能出色的有着固定大小的集合,以LRU(Least Recently Used 最近最少使用)规则和插入顺序进行age-out(老化移出)处理,自 ...
- 转 Delphi中XLSReadWrite控件的使用(2)---基本应用
unit Main; interface uses Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms, ...
- Ubuntu的Unable to locate package无法更新源问题解决方案
https://blog.csdn.net/long19910605/article/details/47017889/ 问题: 更新源时提示不能联网(does the network require ...
- Sobel算法
最近看了一些Sobel算法,并试了一下,源码如下: private void Sobel(Bitmap img) { int width = img.Width; int height = img.H ...
- c++缓冲区------c++ Primer Plus
通常,通过使用缓冲区可以更高效地处理输入和输出.缓冲区是用作中介的内存块,它是将信息从设备传输到程序或从程序传输给设备的临时存储工具.通常,像硬盘驱动器这样的设备以512字节(或更多)的块为单位来传输 ...
- linux 改变系统时间
date 查看系统时间 date -s 04/05/16 日期设置成2016年4月5日 date -s 15:03:32 日期设置成2016年4月5日15:03:32 上述两步可以直接写成这样一 ...
- The method identifyUser(Arrays.asList("group001"), String, new HashMap<>()) is undefined for the type AipFace
在使用百度云的人脸识别sdk时遇到了这个错误,网上百度不到解决的方法,当我浏览百度云的时候发现了这个 于是考虑到版本可能更新,出现了新的函数代替旧的函数,于是去查文档,文档链接如下 https://c ...
