Wolfram常用计算

1.方程与方程组

例1：求解方程

参考表达式：

solve x^3 + 2x^2 - 6x + 5 = 0 real

求解所有根

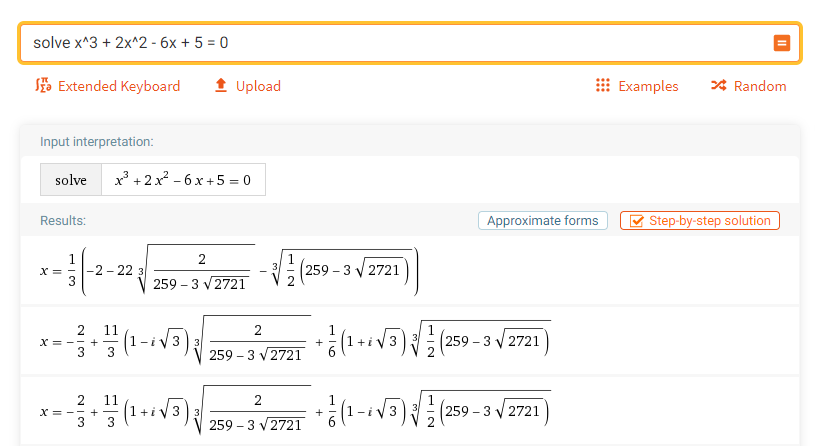
例2：求解方程：

参考表达式：

solve ax^2+bx+c=0

注：默认求解以x为变量的方程，也可指定变量求解

如：求解以a为变量的方程

例3：求解方程组：

参考表达式：

solve x+y+z=1,x^2+y^2+z^2=1,x^3+y^3+z^3=1 for x,y,z

2.不等式与不等式组

例1：求解一元二次不等式

参考表达式：

solve x^2+x-6>0

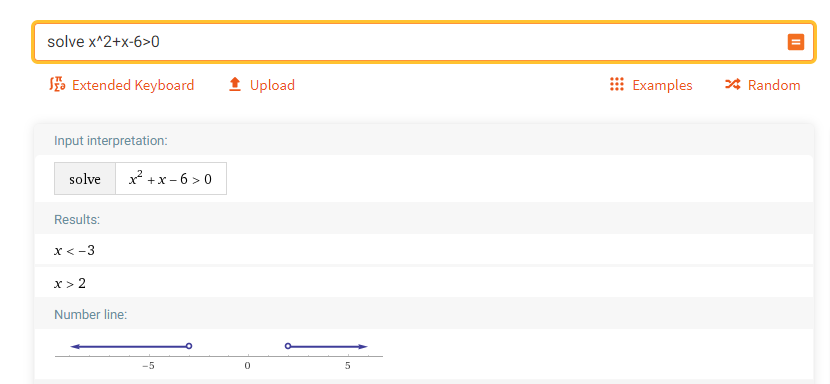
例2：求解一元一次不等式组

参考表达式：

solve 2x+6>7x-9, (4x+2)/5>=(x-1)/2

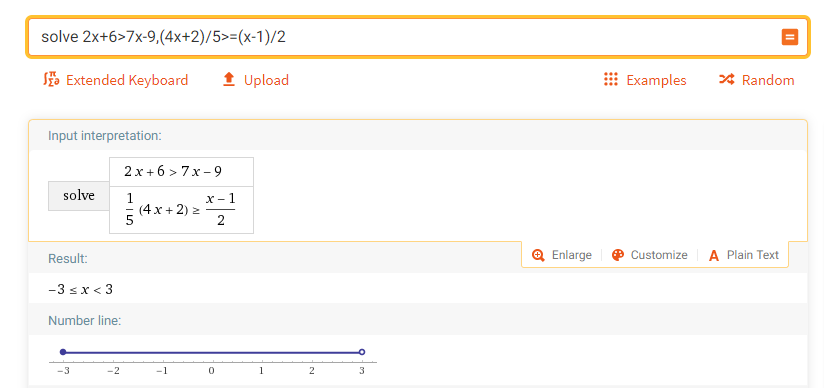
例3：求解二元一次不等式组

参考表达式：

solve x-y>=0,x+2y-4<=0,y+2>=0

3.多项式系列

例1：分解下列多项式

参考表达式：

factor 3x^4-2x^3y+3x^3-x^2y^2-2x^2y+6x^2-xy^2-4xy-2y^2

例2：求最大公因式

参考表达式：

gcd x^4-9x^2-4x+12,x^3+5x^2+2x-8

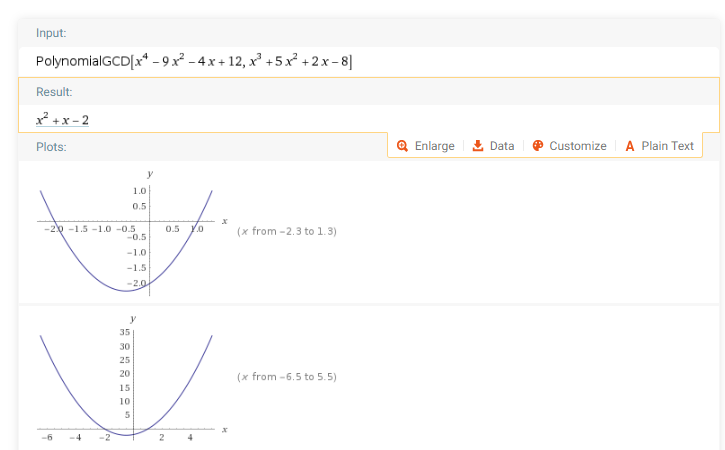
例3：配方

参考表达式：

complete the square ax^2+bx+c

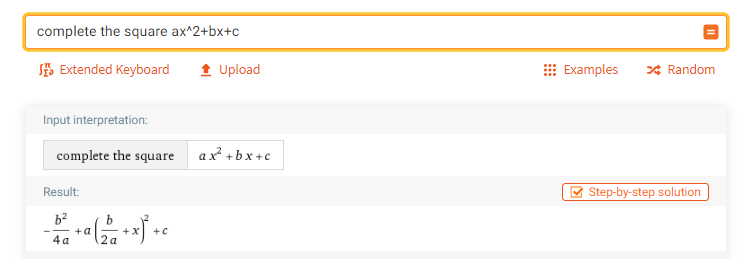
例4：有理式通分

参考表达式：

together a/(ax+b)+1/(x^2+2x-1)

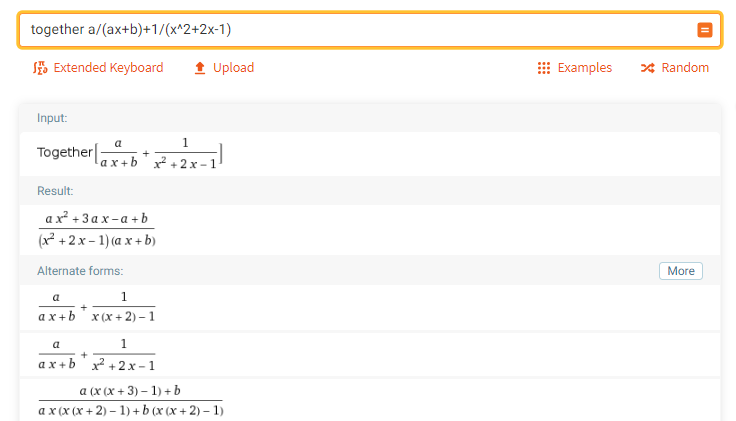
例5：有理式分解

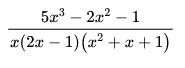
参考表达式：

apart (-1-2x^2+5x^3)/(x (-1+2x) (1+x+x^2))

4.函数定义域与值域

例1：求解下列函数定义域和值域

参考表达式：

domain of f(x,y) = log(y-x)+(x^(1/2))/((1-x^2-y^2)^(1/2)))

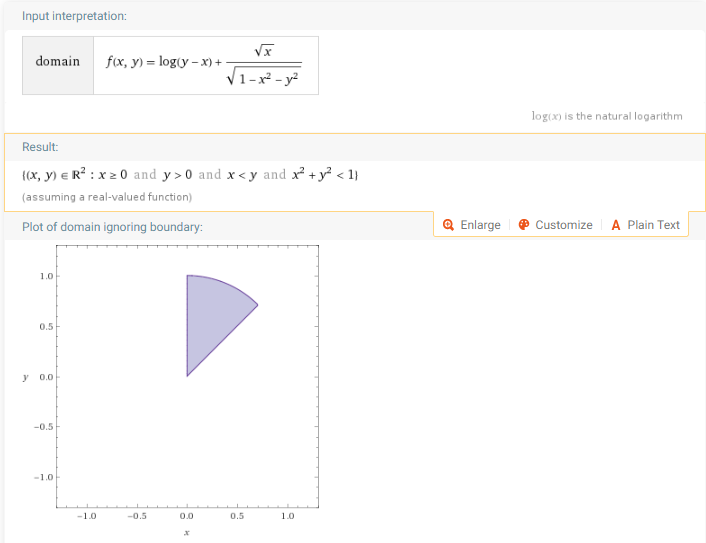
5.数列极限

例1：计算下列数列极限

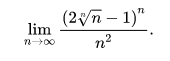
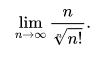
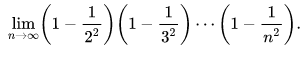
参考表达式：

lim ((2n^(1/n)-1)^n)/(n^2), n->infinity

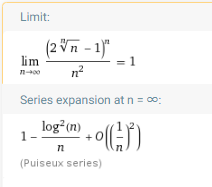
lim n/((n!)^(1/n)), n->infinity

lim sum(1/(k^(1/2)),k=n^2 to (n+1)^2),n->infinity

product 1-1/k^2,k=2 to n,n->Infinity

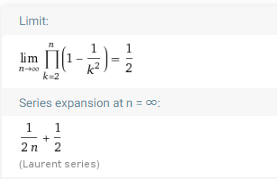
6.函数极限与连续性

例1：一元函数极限

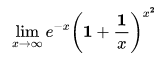
参考表达式：

lim (e^(-x))*(1+1/x)^(x^2), x->infinity

例2：多元函数极限

参考表达式：

lim log(x+e^y)/((x^2+y^2)^(1/2)), (x,y)->(1,0)

例3：函数间断点与类型

从函数表达式可以看到x=0,x=±1为其间断点，输入表达式：

lim (x^2-x)/(|x|(x^2-1)), x->0-

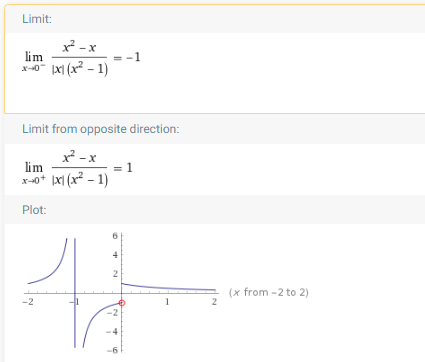
所以x=0是跳跃间断点

输入表达式：

lim (x^2-x)/(|x|(x^2-1)), x->-1+

所以x=±1是无穷间断点

7.函数的导数

例1：一元函数的一阶导数及导数值

计算以下函数的导数，并求在x=1处的导数值

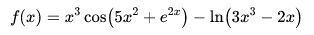
输入表达式：

d/dx((x^3)cos(5x^2+e^(2x))-ln(3x^3-2x)) where x=1

例2：一元函数的高阶导数

计算以下函数的50阶导数：

输入表达式：

d^50/dx^50((x^2)cosx)

例3：复合函数的导数

1)计算下列函数的一阶、二阶导数

输入表达式：

d/dx (x^2)f(3x+4cosx)

d^2/dx^2 (x^2)f(3x+4cosx)

2)求下列函数的混合偏导数

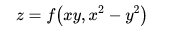
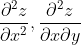
输入表达式：

d^2/dx^2 f(xy, x^2-y^2)

d/dx d/dy f(xy, x^2-y^2)

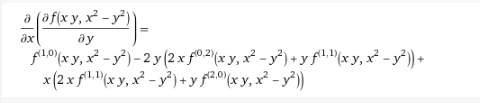
例4：隐函数的导数

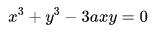
输入表达式：

derivative x^3+y^3-3axy=0 with respect to x

例5：参数方程的导数

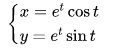
输入表达式：

(d/dt e^t sint)/(d/dt e^t cost)

例6：多元函数的导数

求以下函数关于x的三阶偏导数与关于y的二阶偏导数的混合高阶偏导数

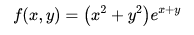
输入表达式：

d^3/dx^3 ((x^2+y^2)e^(x+y))

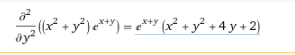
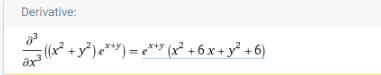
8.函数单调性和临界点

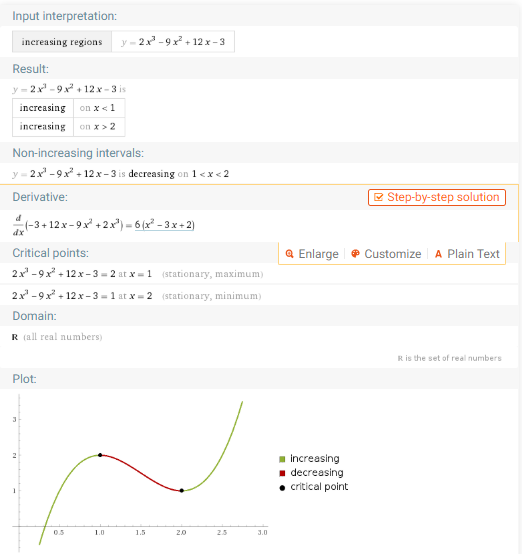
求下列函数的单调区间

输入表达式：

where is 2x^3-9x^2+12x-3 increasing

9.函数驻点与拐点

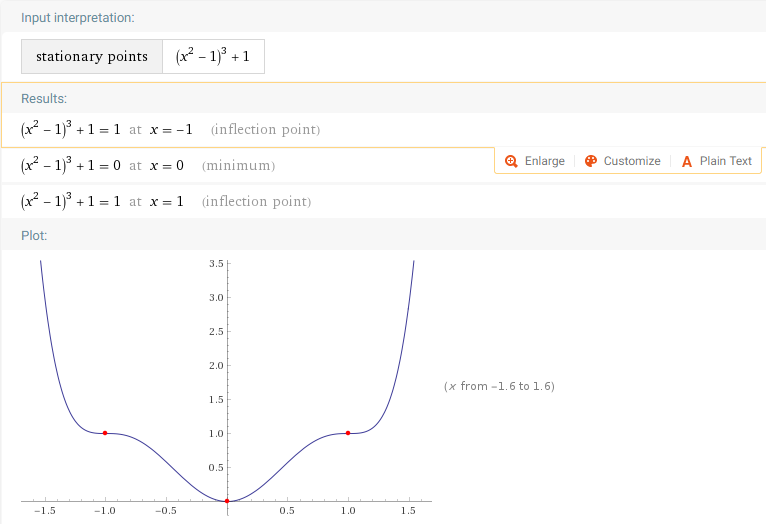
计算以下函数的驻点和拐点

输入表达式：

stationary points of (x^2-1)^3+1

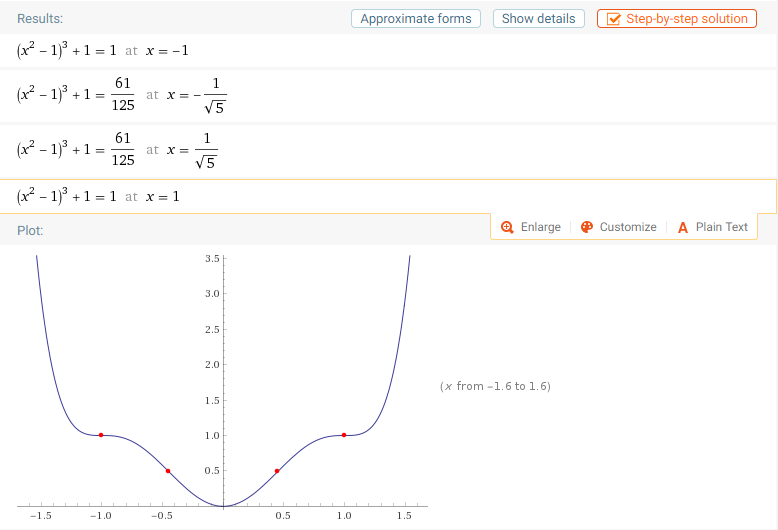
10.函数极值与最值

1)一元函数极值

计算以下函数极值点和极值

输入表达式：

local extrema x^4-8x^2+2

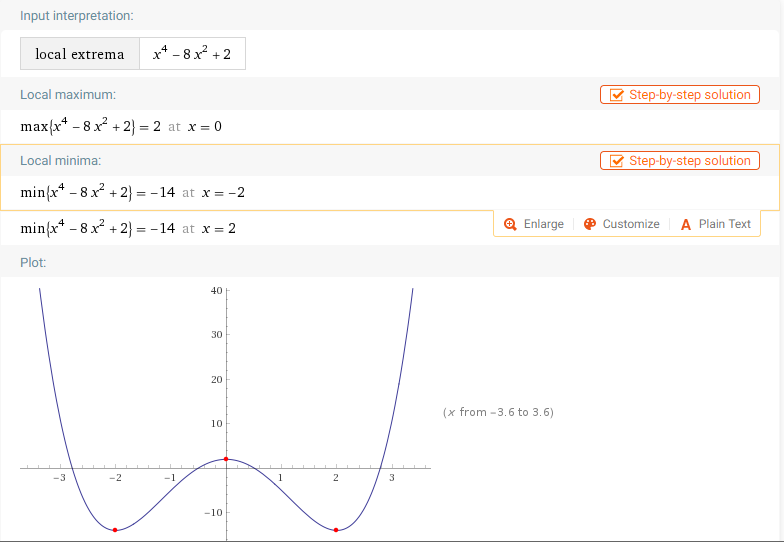
2)一元函数最值

求下列函数在指定范围内的最值

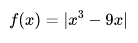
输入表达式：

maximize |x^3-9x|,-3<=x<=5

minimize |x^3-9x|,-3<=x<=5

3)多元函数极值

计算以下函数的驻点/极值点和极值

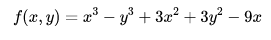
输入表达式：

stationary points of x^3-y^3+3x^2+3y^2-9x

local extrema x^3-y^3+3x^2+3y^2-9x

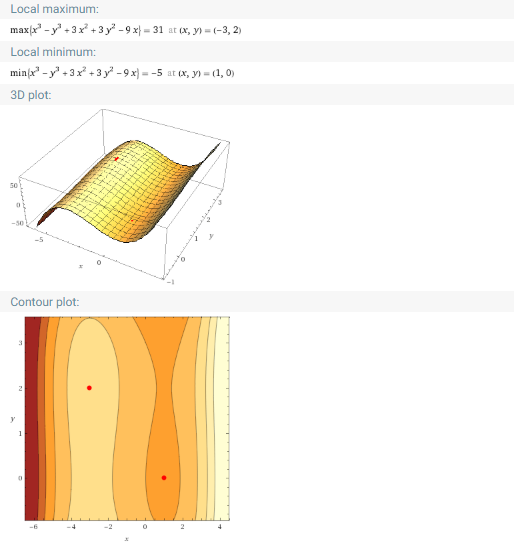
4)多元函数最值

求下列函数在指定范围内的最值

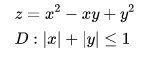
输入表达式：

maximize x^2+y^2-x y on |x|+|y|<=1

minimize x^2+y^2-x y on |x|+|y|<=1

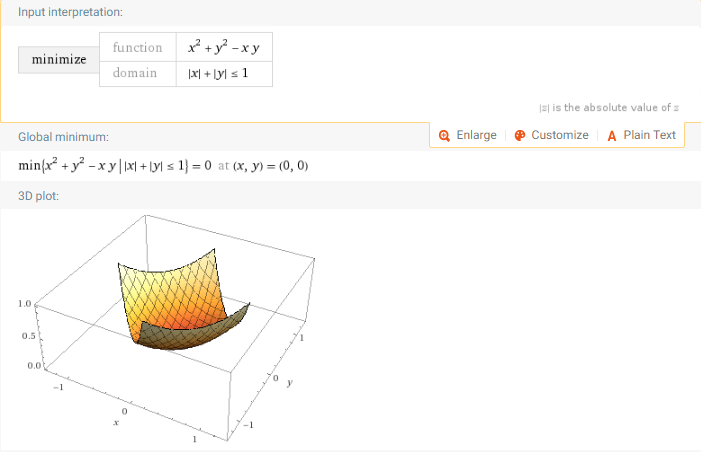
11.全微分计算

计算以下函数的全微分

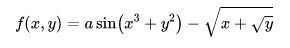
输入表达式：

derivative of asin(x^3+y^2)-(x+y^(1/2))^(1/2)

12.方向导数计算

计算以下函数指定方向和点处的方向导数

输入表达式：derivative 3x^2+2y^2+z^2 in direction (-2,-2,1) at point (1,2,3)