Educational Codeforces Round 151 (Rated for Div

C. Strong Password

给定一个字符串\(s\)，一个密码的长度\(m\)，下界字符串\(l\)和上界字符串\(r\)，上下界字符串长度均为\(m\)，且字符只在0~9范围内，上界字符串的第 \(i\) 位非严格大于下界字符串的第 \(i\) 位，密码的第 \(i\) 位需要位于 \([l_i, r_i]\) 内。问是否存在一个密码不是\(s\)的子序列？

\(1 \leq m \leq 10\)

\(1 \leq |s| \leq 3\times 10^5\)

题解：贪心 + 枚举

• 因为\(m\)的范围比较小，所以我们不妨考虑枚举密码的每一位
• 根据题意得知，第\(i\)位密码\(ch\)必须保证在\([l_i,r_i]\)范围内
• 因为题目给出的是子序列，所以我们一旦选定了第\(i\)位密码为\(ch\)，假设\(ch\)在\(s\)中存在且第一次出现的位置为\(pos\)，那么第\(i+1\)位密码应该从\(s\)的第\(pos\)位之后开始搜索
• 我们不妨设\(s\)的第\(pos\)位之后的部分字符串为\(t\)
• 如果我们枚举到的密码在\(t\)中不存在，那么说明密码一定能被构造出来
• 如果第\(i\)位密码的所有情况在\(t\)中都存在的话，我们贪心地选择\([l_i,r_i]\)中第一次出现且在\(s\)中下标最大的字符作为第\(i\)位密码

#include <bits/stdc++.h>
#define Zeoy std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0)
#define all(x) (x).begin(), (x).end()
#define rson id << 1 | 1
#define lson id << 1
#define int long long
#define mpk make_pair
#define endl '\n'
using namespace std;
typedef unsigned long long ULL;
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<double, double> pdd;
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3f;
const int mod = 1e9 + 7;
const double eps = 1e-9;
const int N = 2e5 + 10, M = 4e5 + 10;

void solve()
{
    string s;
    cin >> s;
    int m;
    cin >> m;
    string l, r;
    cin >> l >> r;
    bool flag = false;
    int p = 0;
    for (int i = 0; i < m; ++i)
    {
        int mx = 0;
        for (char j = l[i]; j <= r[i]; ++j)
        {
            int t = s.find(j, p);
            if (t == -1)
            {
                flag = true;
                break;
            }
            mx = max(mx, t);
        }
        p = mx + 1;
        if (flag)
        {
            cout << "YES" << endl;
            return;
        }
    }
    cout << "NO" << endl;
}
signed main(void)
{
    Zeoy;
    int T = 1;
    cin >> T;
    while (T--)
    {
        solve();
    }
    return 0;
}

D. Rating System

给定对局数\(n\)，以及每个对局会使得\(rating\)的变化值\(a_i\)，初始\(rating\)为\(0\)。问给定的低保线\(k\)（分数到\(k\)后无论\(rating\)怎么变不会低于\(k\)）为多少时，\(n\)个对局后玩家的\(rating\)最高

题解：思维 + 最大后缀

• 容易发现答案应该是前缀和\(pre_i\)中的一个，但是如果我们枚举所有的前缀和复杂度显然为\(O(n^2)\)，所以我们不妨逆向思维来考虑这个问题
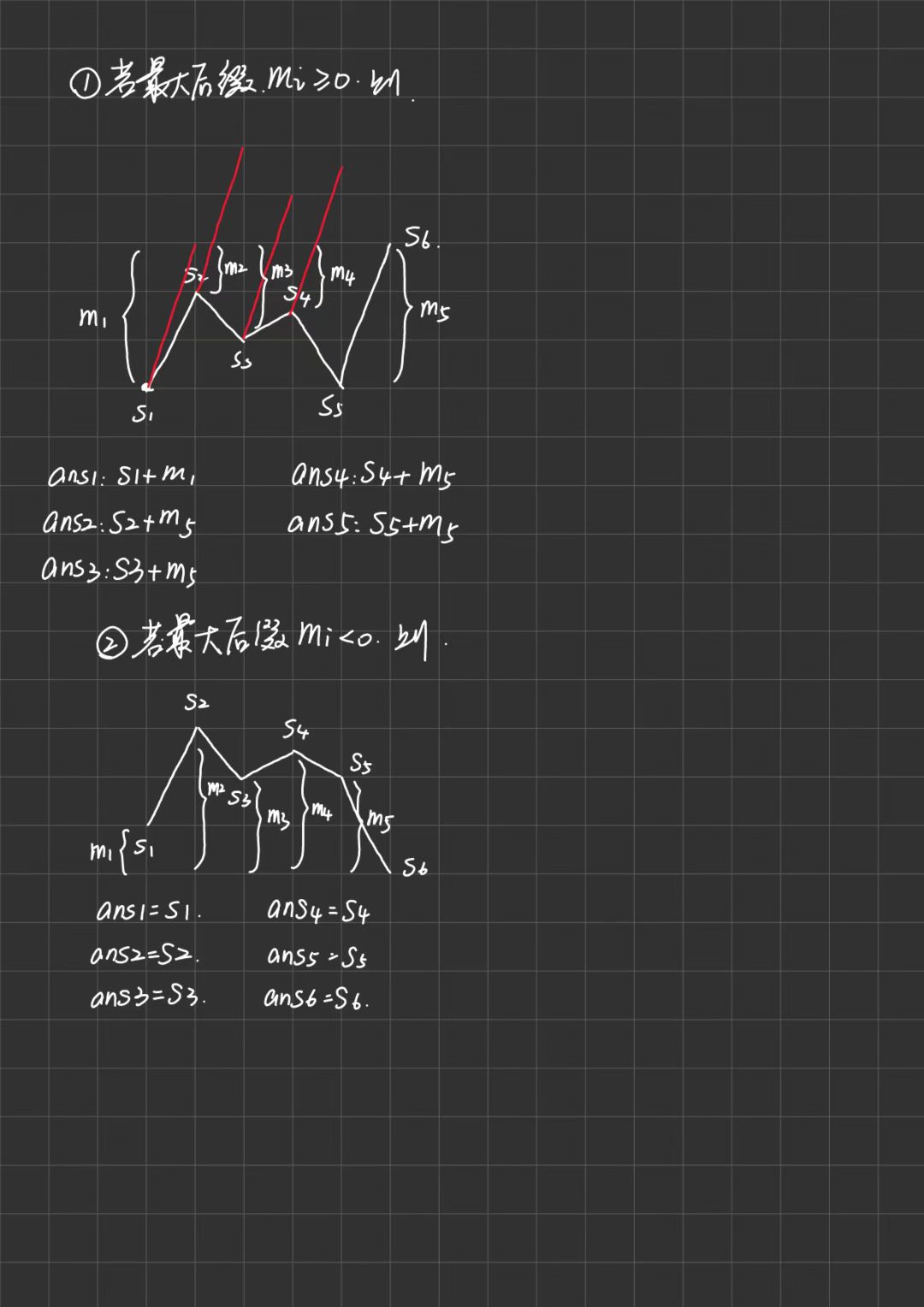
• 设\(suf\_max_i\)为第\(i\)位之后的最大后缀，易得\(suf\_max[i] = max(suf[i+1],pre[n]-pre[i])\)
• 我们手模发现，对于任意一个\(k = pre_i\)，最终的\(rating\)为\(pre_i + suf\_max_i\)
• 
• 这样的话，时间复杂度为\(O(n)\)

#include <bits/stdc++.h>
#define Zeoy std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0)
#define all(x) (x).begin(), (x).end()
#define rson id << 1 | 1
#define lson id << 1
#define int long long
#define mpk make_pair
#define endl '\n'
using namespace std;
typedef unsigned long long ULL;
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<double, double> pdd;
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3f;
const int mod = 1e9 + 7;
const double eps = 1e-9;
const int N = 3e5 + 10, M = 4e5 + 10;

int n;
int a[N];
int pre[N];

void solve()
{
    cin >> n;
    for (int i = 1; i <= n; ++i)
        cin >> a[i];
    for (int i = 1; i <= n; ++i)
        pre[i] = pre[i - 1] + a[i];
    vector<int> suf_max(n + 10);
    for (int i = n; i >= 0; i--)
        suf_max[i] = max(suf_max[i + 1], pre[n] - pre[i]);
    int k = 0;
    for (int i = 1; i <= n; ++i)
    {
        if (pre[k] + suf_max[k] < pre[i] + suf_max[i])
            k = i;
    }
    cout << max(0LL, pre[k]) << endl;
}
signed main(void)
{
    Zeoy;
    int T = 1;
    cin >> T;
    while (T--)
    {
        solve();
    }
    return 0;
}