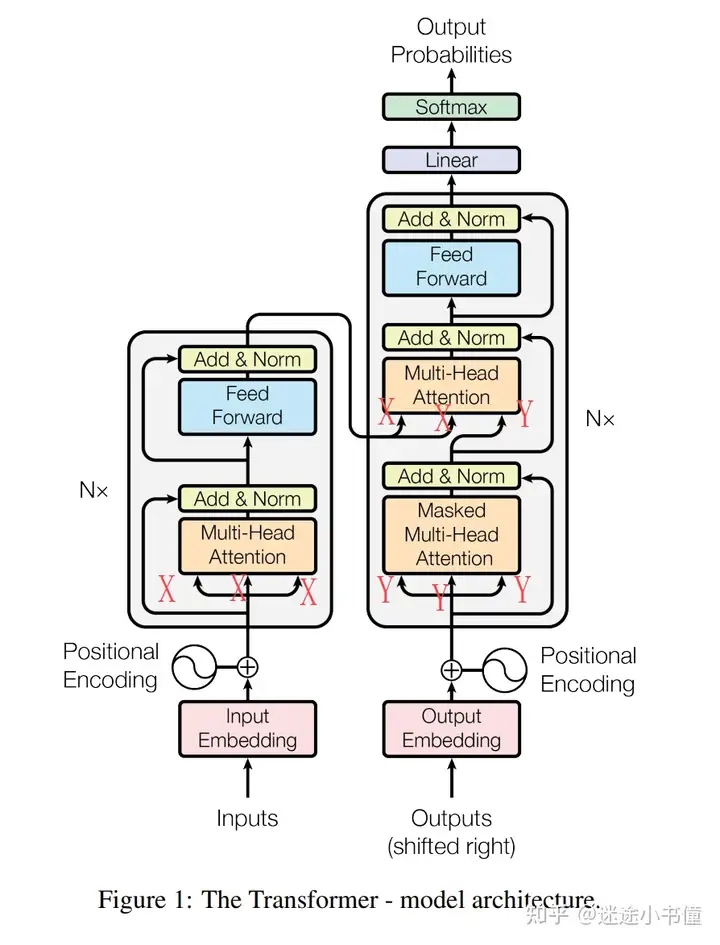
SciTech-BigDataAIML-LLM-Transformer Series-Self-Attention:由Dot-Product(向量点乘)说起
本文公式中变量加粗表示该变量为向量或矩阵
Softmax后每个值\(\in [0, 1)\)且总和为0
经过Softmax的归一化后:
- 每个值是一\(\in [0, 1)\)的权重系数(可理解成一"权重矩阵").
- 且总和为0.
初学Transformer都问Q, K, V怎么来的
把修正前的公式与图 和 真正 "符合代码实现"的 "图与公式" 分别对比, 发现原始论文的图, 绘制的不标准. 原论文: Attention is all you need: https://arxiv.org/pdf/1706.03762.pdf
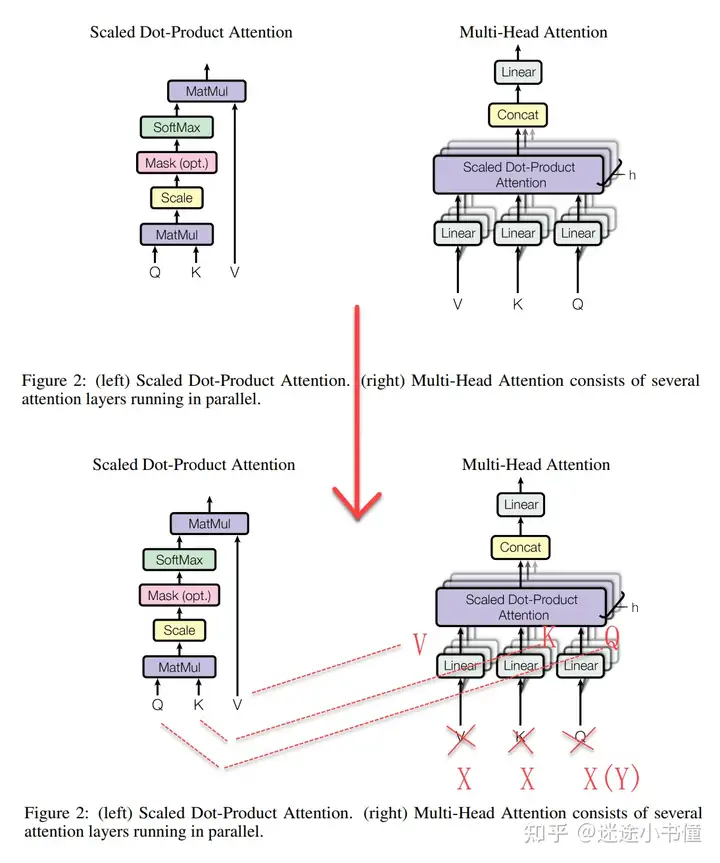
最重要的上图, 绘制的有问题:
- 右边MHA(multi-head attention)的输入的Q, K, V 和
- 左边SDPA(Scaled Dot-Product Attention)的三个输入 Q, K, V,
根本不是一个东西, 这个最容易引起误导。
"右边MHA的Q, K, V" 是经过 "三层线性层" 之后的结果。
而 "三个线性层" 之后得到的, 才是和 "左边SDPA的Q, K, V" 可以一一对应的。
右边MHA的输入( Q, K, V)可能是:
- X, X, X (自注意力)
- X, X, Y (交叉注意力)。
以 Machine Translation Task 为例, - X来自source language sequence,
- Y来自target language sequence。
当然,如果是SA(Self-Attention自注意力),
那么右边MHA(Multi-Head Attention)的三个输入都是同一矩阵: X, X, X。
如果是MSA(Masked Self-Attention), 那么都是Y, Y, Y。见下图:
![]()
区分,SA(X, X, X), 以及 MSA(Y, Y, Y),以及交叉注意力(X, X, Y)。
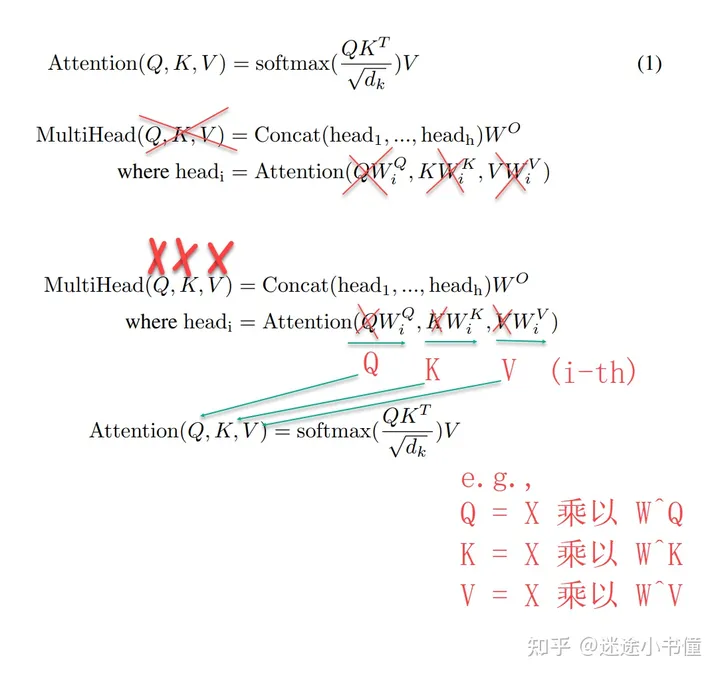
同理,论文的公式,也一样有问题:

上面的公式,让函数Attention 和 MultiHead 都用Q, K, V作为输入, 容易误导初学者。
把上面公式的 MultiHead函数 的输入, 替换成如下更易理解:
- X, X, X( encoder的自注意力),
- Y, Y, Y(decoder的SA自注意力),
- X, X, Y(decoder里面的交叉注意力),
三个线性层,用W矩阵表示了,即\(\large \bf{W_{Q},\ W_{K},\ W _{V}}\):
Self Attention:由Dot-Product(向量点乘)说起
由Dot-Product(向量点乘)起讲 Transformer Self-Attention
Transformer[1]论文提出了一种Self-Attention自注意力机制), Self-Attention的最核心的公式为:
\(\large \begin{align*} \\
& Attention(Q,K,V)=Softmax( \frac{QK^⊤}{\sqrt{d_k}} )V \\
& where, Q : Query,\ K : key,\ V : Value \\
\\
\end{align*} \\
\)
单看这个公式,其实并不能很好地理解Attention到底在做什么,
本文从Transformer所使用的Self-Attention,介绍Attention背后的原理。
Self-Attention:从向量点乘说起
我们先从:\(\large Softmax(XX ^⊤)X\)这样一个公式开始。
\(\large Dot\ Product\)
1 \(\large Dot\ Product \ for Vectors\)
首先需要复习\(\large Dot\ Product\)(向量点乘)的概念。对于两个\(\large 行向量x和y\):
\(\large \begin{align*} \\
\bf{x} &=[& x_0 &, & x_1 & , & \cdots &, & x_n &] \\
\bf{y} &=[& y_0 &, & y_1 & , & \cdots &, & y_n &] \\
\bf{x \cdot y} &= & x_0 \cdot y_0 & + & x_1 \cdot y_1 & + & \cdots & + & x_n \cdot y_n &\ \\
\end{align*} \\
\)
向量点乘的几何意义是:
向量 \(\large \bf{x}\) 在向量 \(\large \bf{y}\) 方向上的投影向量 与向量\(\large \bf{x}\) 的乘积.
向量点乘能够反映两个向量的相似度。点乘结果越大,两个向量越相似。
2 $\large Dot\ Product \ for Matrices $
一个矩阵 \(\large \bf{X}\) 由 \(\large {n}\) 行向量组成。
比如,我们可以将某一行向量 \(\large \bf{X_i}\) 理解成一个词的词向量,
共有 \(\large {n}\) 个行向量组成 \(\large {n \times n}\)的方形矩阵:
\(\large \begin{align*} \\
\bf{X} = \begin{bmatrix} X_0 \\
X_1 \\
\vdots \\
X_n \\
\end{bmatrix} \text{, then } \bf{X^T} = \begin{bmatrix} X_0^T, X_1^T, \cdots, X_n^T \end{bmatrix} \\
\end{align*} \\
\)
矩阵 \(\large \bf{X}\) 与矩阵的转置 \(\large \bf{X^T}\) 矩阵乘法:
\(\large \bf{X}\) 的\(第\)i\(行\)与 \(\large \bf{X^T}\) 的$ 第\(j\)列$相乘, 得到 \(目标矩阵\bf{Y}\) 的\(一个元素 Y_{ij}\),
$\large \bf{X} \bf{X^T} $ 可表示为:
\(\large \begin{align*} \\
\bf{Y} = \bf{X} \bf{X^T} = \begin{bmatrix} X_0 \cdot X_0,& X_0 \cdot X_1, & \cdots, & X_0 \cdot X_n \\
X_1 \cdot X_0, & X_1 \cdot X_1, & \cdots, & X_1 \cdot X_n \\
\vdots & \vdots & & \vdots \\
X_n \cdot X_0, & X_n \cdot X_1, & \cdots, & X_n \cdot X_n \\
\end{bmatrix} \\
\end{align*} \\
\)
$\large \bf{X} \bf{X^T} $ 的任一元素 \(\large \bf{ X_{ij} }\) , 是向量 \(\large \bf{X_i}\) 与 \(\large \bf{X_j}\) 做\(Dot Product\)(点乘):
\(第1行第1列元素\) , $\large x_0 \cdot x_0 $ , 就是 \(\large x_0\) 自身与自身的相似度,
\(第1行第2列元素\) , $\large x_0 \cdot x_1 $ , 就是 \(\large x_0\) 与 \(\large x_1\) 的相似度。
\(\large Softmax(XX ^⊤)X\)三步曲
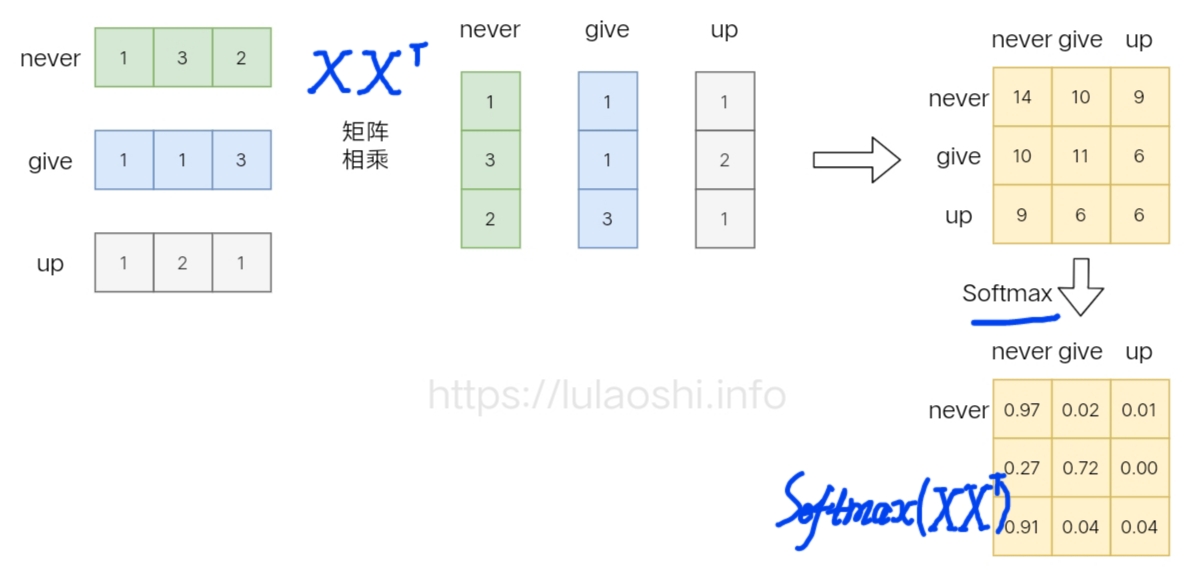
1 词向量矩阵 与自身的转置"矩乘"生成相似度矩阵
下面以词向量矩阵为例,这个矩阵的每行为一个词的词向量。
矩阵与自身的转置"矩乘",生成目标矩阵(就是一个词的词向量与各个词的词向量的相似度。
2 Softmax归一化相似度矩阵(词向量矩阵的)
如果再加上Softmax呢?我们先计算\(\large Softmax(XX ^⊤)\)。
Softmax的作用是对向量做归一化(就是对相似度的归一化), 得到一个归一化的权重矩阵,
矩阵中,某个值(权重)越大,表示相似度越高。
3 Softmax归一化的相似度矩阵 与 原词向量矩阵的矩乘 加权求和
在这个基础上,再进一步计算:\(\large Softmax(XX ^⊤)X\)
将得到的归一化的权重矩阵, 与词向量矩阵做"矩乘"。
权重矩阵的:
- 某一行 分别与 词向量的一列 矩乘,
- 词向量矩阵的一列 代表着任一不同词的某一维度。
经过如此矩阵乘法,就是一个加权求和的过程:
- 结果词向量, 是经过加权求和之后的新表示;
- 权重矩阵, 是通过相似度和归一化两步计算得到的。
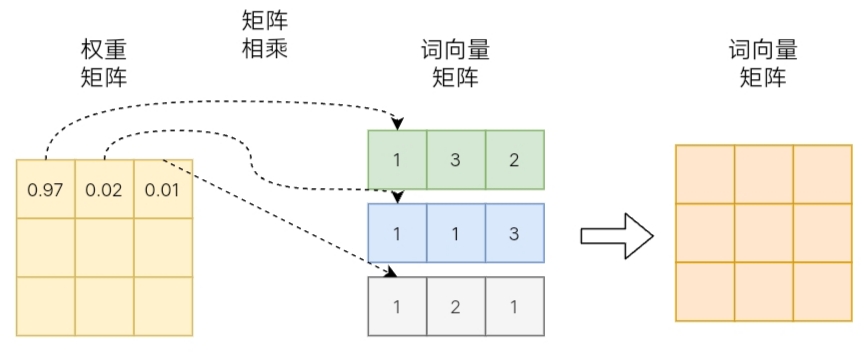
通过与权重矩阵相乘,完成加权求和过程
4 上述过程用 PyTorch 实现
import torch
import torch.nn as nn
x = torch.tensor([[1, 3, 2], [1, 1, 3], [1, 2, 1]], dtype=torch.float64)
attention_scores = torch.matmul(x, x.transpose(-1, -2))
attention_scores = nn.functional.softmax(attention_scores, dim=-1)
print(attention_scores)
Self-Attention的Q、K、V
注意力Attention机制的最核心的公式为:
\(\large \begin{align*} \\
& Attention(Q,K,V)=Softmax( \frac{QK^⊤}{\sqrt{d_k}} )V \\
& where, Q : Query,\ K : key,\ V : Value \\
\\
\end{align*} \\
\)
与我们刚才分析的 \(\large Softmax(XX ^⊤)\) 和 \(\large Softmax(XX ^⊤)X\) 有几分相似。
Transformer论文中将这个Attention公式描述为:"Scaled" Dot-Product Attention。
V是从哪儿来的呢?
在Transformer的Encoder所使用的, , , 其实都是从"同一输入矩阵" 线性变换而来的。
我们可以简单理解成:\(\large \bf{ Q =X W_Q,\ K =X W_K,\ V =X W_V \ }\)
其中,\(\large \bf{W_Q,\ W_K,\ W _V}\)是三个可训练的参数矩阵。
输入矩阵 \(\large \bf{X}\) 分别与 \(\large \bf{W_Q,\ W_K,\ W _V}\) 矩乘 生成 \(\large \bf{Q、K、V}\),近似于一次线性变换。
Attention不直接使用\(\large \bf{X}\),而是使用经过矩阵乘法生成的这三个矩阵,
是因为使用三个可训练的参数矩阵,可增强模型的拟合能力。
Self-Attention可以解释一个句子内不同词的相互关系。
比如下面的句子,“eating”后面会有一种食物,
“eating”与“apple”的Attention Score更高,
而“green”只是修饰食物“apple”的修饰词,和“eating”关系不大。
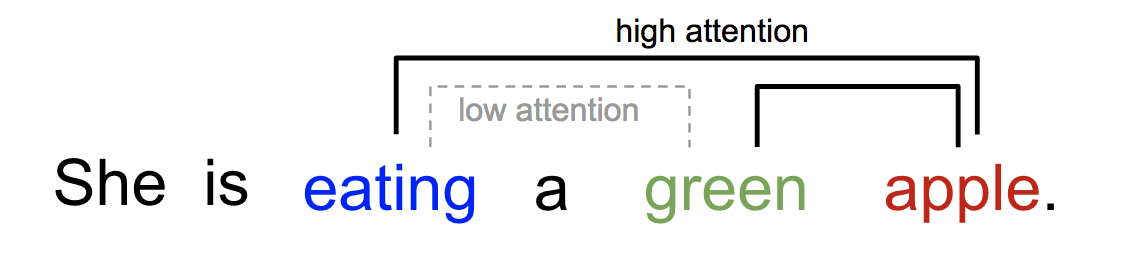
句子内不同词之间的Attention示意图
下面这张图是Transformer论文中描述Attention计算过程的示意图。
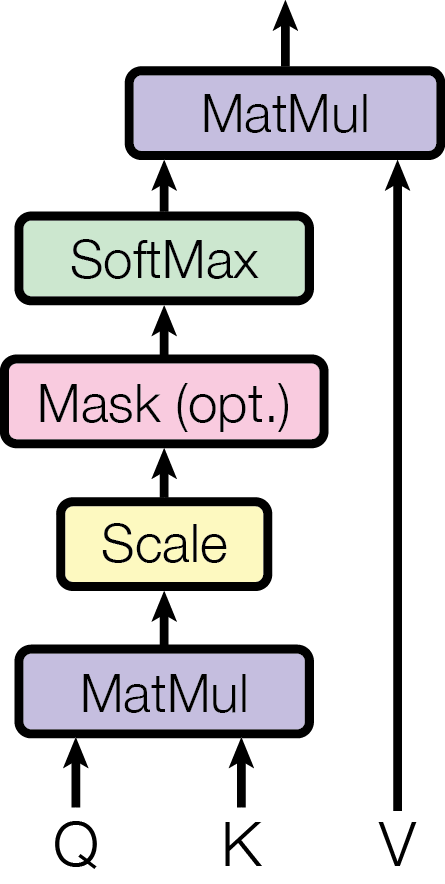
在上图,\(\large \bf{Q}\)与\(\large \bf{K^T}\)经过MatMul,生成相似度矩阵。
对相似度矩阵每个元素除以\(\large \sqrt{d_k}\) ( 这个除法被称为Scale ),
\(\large d_k\) 是 \(\large \bf{K^T}\)的维度大小), 得到\(\large Attention\ Score\ Vector\)。
当 \(\large d_k\) 很大时,\(\large \bf{QK^T}\)的乘法结果方差变大,
Scale可以使结果相似度矩阵的方差稳定,训练时梯度更新更稳定。
MHA(Multi-Head Attention)多头注意力
1 MHA 原理
为增强拟合性能, Transformer继续扩展Attention, 提出MHA(Multiple Head Attention, 多头注意力)。
刚才我们已经理解:
- \(\large \bf{ Q =X W_Q,\ K =X W_K,\ V =X W_V \ }\)
- \(\large \bf{W_Q,\ W_K,\ W _V}\)是三个可训练的参数矩阵。
- 输入矩阵\(\large X\)分别与 \(\large \bf{W_Q,\ W_K,\ W _V}\) 矩乘生成\(\large \bf{Q、K、V}\),近似于一次线性变换。
- Attention不直接使用\(\large \bf{X}\),而是使用经过矩阵乘法生成的这三个矩阵,
是因为使用三个可训练的参数矩阵,可增强模型的拟合能力。
现在,对同一输入 \(\large \bf{X}\) , 我们定义多组不同的 \(\large \bf{W_{Q},\ W_{K},\ W _{V}}\) ,比如:
\(\large \bf{W_{Q0},\ W_{K0},\ W _{V0}}\) 与 \(\large \bf{W_{Q1},\ W_{K1},\ W _{V1}}\) ,
每组分别计算生成不同的\(\large \bf{Q,\ K,\ V}\), 最后学习到不同的参数。
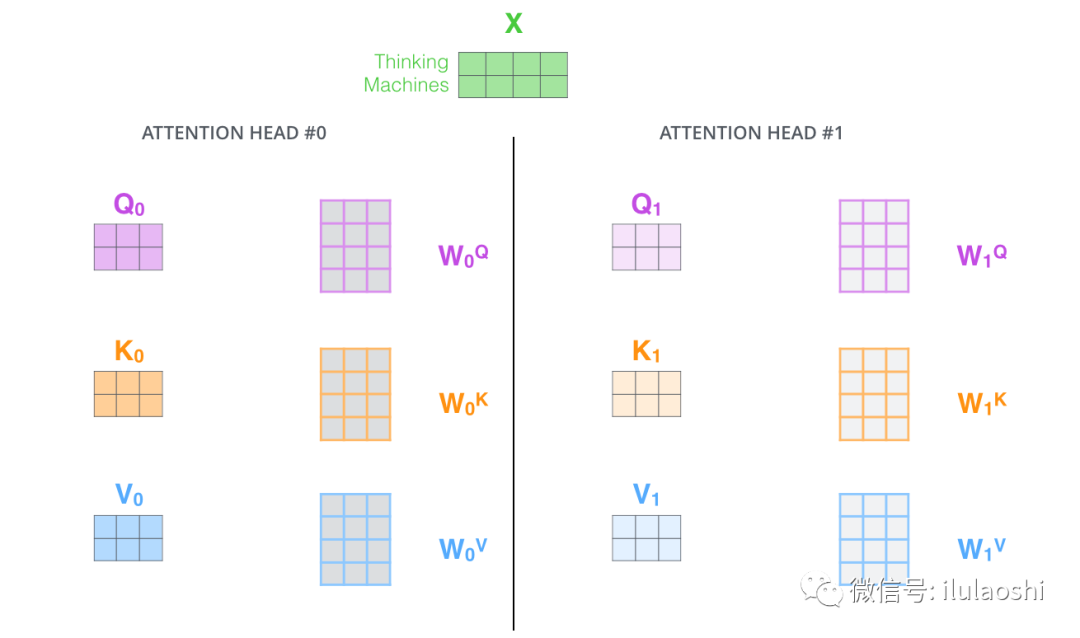
2 多组\(\large \bf{W(Weight\ Parameter)}\) 得多组\(\large \bf{Q,\ K,\ V}\)
比如我们定义8组 \(\large \bf{W}\), 同一输入 \(\large \bf{X}\) , 将得到8个不同的输出: \(\large \bf{Z_0}\) 到 \(\large \bf{Z_0}\)
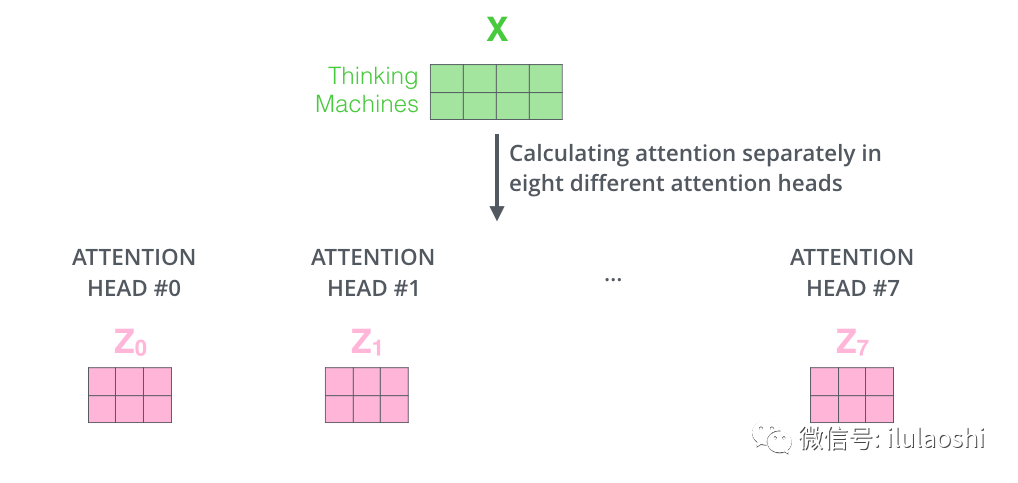
假如定义8组参数
在输出到下一层前,我们需要将8个输出拼接到一起,
乘以矩阵 \(\large \bf{W_O}\) , 将维度降低回我们想要的维度。
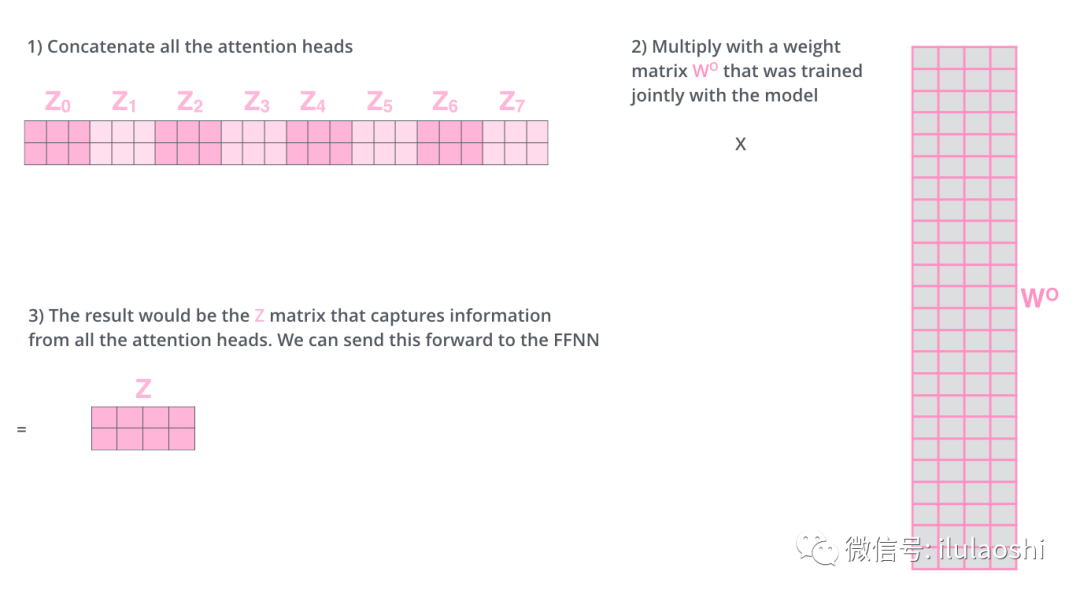
将多组输出拼接后乘以矩阵 \(\large \bf{W_O}\) 以降低维度
多头注意力的计算过程如下图所示。对于下图中的第2)步,
- 当前为第一层时,直接对输入词\(\large \bf{WE}\)(Word Embedding), 生成词向量\(\large \bf{X}\);
- 当前为后续层时,直接使用上一层输出。
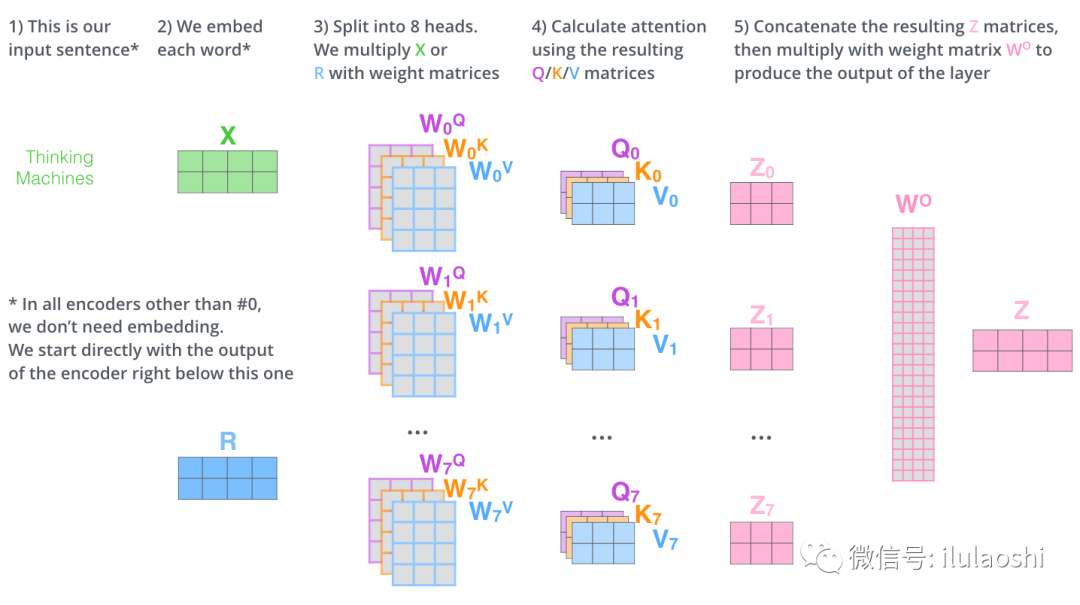
多头注意力计算过程
再去观察Transformer论文给出的多头注意力图示, 更容易理解:
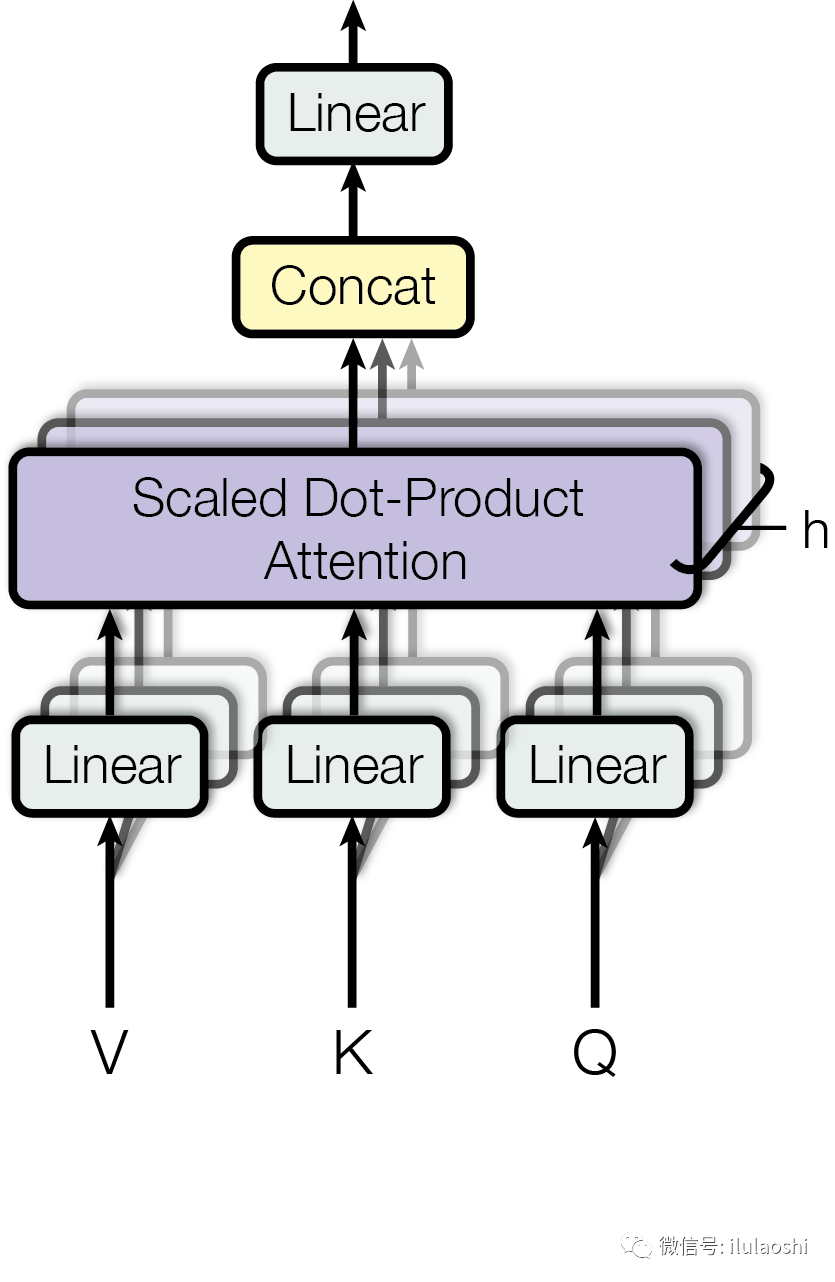
SciTech-BigDataAIML-LLM-Transformer Series-Self-Attention:由Dot-Product(向量点乘)说起的更多相关文章
- 论文翻译——Attention Is All You Need
Attention Is All You Need Abstract The dominant sequence transduction models are based on complex re ...
- NLP学习(5)----attention/ self-attention/ seq2seq/ transformer
目录: 1. 前提 2. attention (1)为什么使用attention (2)attention的定义以及四种相似度计算方式 (3)attention类型(scaled dot-produc ...
- [阅读笔记]Attention Is All You Need - Transformer结构
Transformer 本文介绍了Transformer结构, 是一种encoder-decoder, 用来处理序列问题, 常用在NLP相关问题中. 与传统的专门处理序列问题的encoder-deco ...
- Attention和Transformer详解
目录 Transformer引入 Encoder 详解 输入部分 Embedding 位置嵌入 注意力机制 人类的注意力机制 Attention 计算 多头 Attention 计算 残差及其作用 B ...
- RealFormer: 残差式 Attention 层的Transformer 模型
原创作者 | 疯狂的Max 01 背景及动机 Transformer是目前NLP预训练模型的基础模型框架,对Transformer模型结构的改进是当前NLP领域主流的研究方向. Transformer ...
- A Survey of Visual Attention Mechanisms in Deep Learning
A Survey of Visual Attention Mechanisms in Deep Learning 2019-12-11 15:51:59 Source: Deep Learning o ...
- 用Python手把手教你搭一个Transformer!
来源商业新知网,原标题:百闻不如一码!手把手教你用Python搭一个Transformer 与基于RNN的方法相比,Transformer 不需要循环,主要是由Attention 机制组成,因而可以充 ...
- 一文看懂Transformer内部原理(含PyTorch实现)
Transformer注解及PyTorch实现 原文:http://nlp.seas.harvard.edu/2018/04/03/attention.html 作者:Alexander Rush 转 ...
- (zhuan) Attention in Neural Networks and How to Use It
Adam Kosiorek About Attention in Neural Networks and How to Use It this blog comes from: http://akos ...
- Paper Reading - Attention Is All You Need ( NIPS 2017 ) ★
Link of the Paper: https://arxiv.org/abs/1706.03762 Motivation: The inherently sequential nature of ...
随机推荐
- HarmonyOS运动开发:如何监听用户运动步数数据
前言 在开发运动类应用时,准确地监听和记录用户的运动步数是一项关键功能.HarmonyOS 提供了强大的传感器框架,使得开发者能够轻松地获取设备的运动数据.本文将深入探讨如何在 HarmonyOS 应 ...
- Sentinel——系统规则(系统自适应保护)
目录 系统自适应保护 系统规则 系统自适应保护 Sentinel 系统自适应保护从整体维度对应用入口流量进行控制,结合应用的 Load.总体平均 RT.入口 QPS 和线程数等几个维度的监控指标,让系 ...
- java设置权限过滤器--防止用户未登录访问某些页面
话不多说,上代码!!! package com.store.web.filter; import java.io.IOException; import javax.servlet.Filter; i ...
- 【记录】smartctl|Linux如何通过smartctl查看有没有坏的磁盘?以及使用时长、电源周期、故障记录等
smartctl是一个用于监测和分析硬盘健康状态的工具,可以用于检测是否存在坏的磁盘.以下是使用smartctl检查磁盘健康状态的步骤: 安装smartctl软件 在Linux系统中,smartc ...
- BootStrap CDN收藏,矢量图标
<!-- 新 Bootstrap 核心 CSS 文件 --> <link href="https://cdn.staticfile.org/twitter-bootstra ...
- C#实现MCP Client 与 LLM 连接,抓取网页内容功能!
前面的课程,我们已经用C#实现了,自己的MCP Client. 下面我们一起来实现,MCP Client与LLM 对接. 一.添加依赖库 目前来说,绝大部分的大模型的API,都是遵循OpenAI的接口 ...
- 浅谈Spring、Spring MVC、Spring Boot和Spring Cloud的关系和区别
Spring 框架就像一个家族,有众多衍生产品,例如 boot.security.jpa等等.但它们的基础都是Spring的IOC和AOP等.IOC提供了依赖注入的容器,AOP解决了面向横切面编程 ...
- QRSuperResolutionNet:一种结构感知与识别增强的二维码图像超分辨率网络(附代码解析)
QRSuperResolutionNet:一种结构感知与识别增强的二维码图像超分辨率网络(附代码解析) 趁着 web开发课程 期末考试前夕,写一篇博客.{{{(>_<)}}} 将我最近所做 ...
- Linux系统安全配置相关
一.说明 最近公司安全部门针对我们的系统从系统组件.系统配置.系统应用容器三个层面对系统进行了整体的扫描,针对系统配置这块,有许多安全配置项,这里在这里记录一下,有需要的直接按照介绍的配置进行相应的修 ...
- OceanBase 正式上线 KubeSphere Marketplace
随着云原生与容器化浪潮全面重塑 IT 基础设施,数据库层的"云原生化"也逐渐从趋势演进为现实需求.近日,OceanBase 开源社区的扩展组件 OceanBase Operator ...