luogu-P5320题解

简要题意

设 \(f(n)\) 表示用多米诺骨牌恰好铺满 \(2\times n\) 的平面的方案数，\(g(n)\) 表示用多米诺骨牌恰好铺满 \(3\times n\) 的平面的方案数；设 \(F(n,k)={f(n)\choose k},G(n,k)={g(n)\choose k}\)，求：

\[\begin{aligned}
ans1={1\over r-l+1}\sum_{i=l}^rF(i,k)\\
ans2={1\over r-l+1}\sum_{i=l}^rG(i,k)
\end{aligned}
\]

题解

\(f\) 和 \(g\) 的公式

首先我们需要表示出 \(f\) 和 \(g\)。\(f\) 是好递推的，我们可以用竖着的一张牌把最后一列直接填满，也可以用两张横着的牌填满最后两列，所以就可以直接得出 \(f\) 的递推式：

\[f(n)=f(n-1)+f(n-2),f(0)=1,f(1)=1
\]

然后列出递推式的特征方程：

\[x^2-x-1=0
\]

解得：

\[\begin{cases}
x_1={1-\sqrt5\over2}\\
x_2={\sqrt5+1\over2}
\end{cases}
\]

设 \(f(n)=A\times x_1^n+B\times x_2^n\)，将 \(f(0)=f(1)=1\) 代入可以求得 \(f\) 的通项公式：

\[f(n)={5+\sqrt5\over10}\left({1+\sqrt5\over2}\right)^n+{5-\sqrt5\over10}\left({1-\sqrt5\over2}\right)^n
\]

现在我们尝试推导一下 \(g\) 式子。首先能发现当 \(2\nmid n\) 时无解，所以我们改一下 \(g\) 的定义，设 \(g(n)\) 表示用多米诺骨牌恰好铺满 \(3\times 2n\) 的平面的方案数。如果我们选择最后不去横跨 \(3\times2\) 的方格那么有 \(g(n)\leftarrow 3\times g(n-1)\)；而如果我们选择横跨第 \(i\) 到第 \(n-1\) 个 \(3\times2\) 的方格，可以发现后半部分只有两种情况如下图。

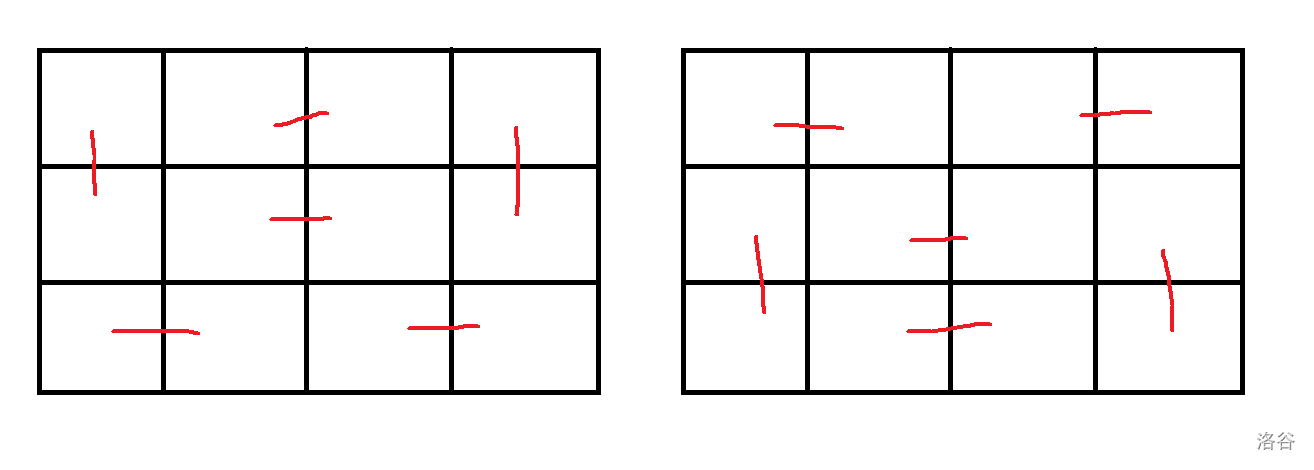
于是对第二种情况我们枚举分界点，可得到完整 \(g\) 的式子：

\[g(n)=3\times g(n-1)+2\sum_{i=0}^{n-2}g(i)
\]

但是呢这个式子实在是太不优美，因为存在 \(O(n)\) 项，于是考虑差分：

\[\begin{aligned}
g(n)-g(n-1)&=3\times g(n-1)-3\times g(n-2)+2\times g(n-2)\\
g(n)&=4\times g(n-1)-g(n-2)
\end{aligned}
\]

求出 \(g\) 的递推式后我们可以依葫芦画瓢得到 \(g\) 的通向式：

\[g(n)={3+\sqrt3\over6}\left(2+\sqrt3\right)^n+{3-\sqrt3\over6}\left(2-\sqrt3\right)^n
\]

后续的推导

求出两个函数的通向式后我们需要解决下面的问题：

\[{1\over r-l+1}\sum_{n=l}^r{Ax_1^n+Bx_2^n\choose k}
\]

因为这里 \(l\) 和 \(r\) 太大了，直接做肯定不行。观察到只有 \(k\) 是小的，所以想把上面的东西变成和 \(k\) 有关的和式。我们先把组合数拆开：

\[ans={1\over(r-l+1)k!}\sum_{n=l}^r\left(Ax_1^n+Bx_2^n\right)^{\underline k}
\]

现在不管和式外面的东西，考虑里面最令人难受的是有一个 k 次下降幂。这启发我们将下降幂转成顺眼的普通幂。斯特林数在此不做展开，如果想学习斯特林数有关的知识这里推荐我的博客。

好了回归正题，我们用下降幂转普通幂就得到：

\[\sum_{n=l}^r\sum_{i=0}^k(-1)^{k-i}{k\brack i}\left(Ax_1^n+Bx_2^n\right)^i
\]

用二项式定理展开最后的普通幂：

\[\sum_{n=l}^r\sum_{i=0}^k(-1)^{k-i}{k\brack i}\sum_{j=0}^i{i\choose j}A^iB^{i-j}\left(x_1^ix_2^{i-j}\right)^n
\]

调一下和式顺序，最后得到：

\[\sum_{i=0}^k(-1)^{k-i}{k\brack i}\sum_{j=0}^i{i\choose j}A^iB^{i-j}\sum_{n=l}^r\left(x_1^ix_2^{i-j}\right)^n
\]

最后面的是等比数列求和，有：

\[\sum_{i=l}^rx^i={x^{r+1}-x^l\over x-1}
\]

记得特判 \(x=1\) 的情况，时间复杂度 \(O(k^2\log r)\)。

对取模意义下根号的处理

在取模意义下并不是所有的数都有二次剩余，所以我们需要寻找新的解决方式。对于此题因为根号下只有一种数，所以我们可以进行一个类似复数的定义：我们将所有数写成 \(a+bi\) 的形式，其中 \(i^2=x\)。举一个例子，若根号下只有 5，也就是 \(f\) 的计算，我们令 \(i^2=5\)，然后类比复数的运算计算答案即可。

代码

const int K = 505, p = 998244353;
int isq;

inline int Add(int x, int y){return x - p + y >= 0 ? x - p + y : x + y;}
inline int Sub(int x, int y){return x < y ? x - y + p : x - y;}
inline int Mul(int x, int y){return 1ll * x * y % p;}
inline int Mo(ll x){return (x % p + p) % p;}

struct cp{int a, b; cp(ll _a = 0, ll _b = 0){a = Mo(_a), b = Mo(_b);}};
inline cp operator + (cp x, cp y){return cp{Add(x.a, y.a), Add(x.b, y.b)};}
inline cp operator - (cp x, cp y){return cp{Sub(x.a, y.a), Sub(x.b, y.b)};}
inline cp operator * (cp x, cp y){return cp{Add(Mul(x.a, y.a), Mul(isq, Mul(x.b, y.b))), Add(Mul(x.a, y.b), Mul(x.b, y.a))};}
inline cp operator ^ (cp x, ll y){cp res = cp(1, 0); for(; y; y >>= 1, x = x * x)if(y & 1)res = res * x; return res;}
inline cp operator / (cp x, cp y){cp t = cp(y.a, - y.b); x = x * t; return x * ((y * t) ^ (p - 2));}
inline bool operator == (cp x, cp y){return x.a == y.a and x.b == y.b;}
inline cp F(cp x, ll l, ll r){return x == cp(1, 0) ? cp(r - l + 1, 0) : ((x ^ (r + 1)) - (x ^ l)) / (x - cp(1, 0));}

cp s1[K][K], C[K][K], fac[K], ifa[K];
cp A, B, x, y;

void prework(){
    s1[0][0] = C[0][0] = C[1][0] = fac[0] = ifa[0] = cp(1, 0);
    for(int i = 1; i < K; ++i)for(int j = 1; j <= i; ++j)s1[i][j] = s1[i - 1][j - 1] + s1[i - 1][j] * cp(i - 1, 0);
    for(int i = 1; i < K; C[++i][0] = cp(1, 0))for(int j = 1; j <= i; ++j)C[i][j] = C[i - 1][j] + C[i - 1][j - 1];
    for(int i = 1; i < K; ++i)fac[i] = fac[i - 1] * cp(i, 0);
    ifa[K - 1] = fac[K - 1] ^ (p - 2);
    for(int i = K - 2; i; --i)ifa[i] = ifa[i + 1] * cp(i + 1, 0);
}
void init(int typ){
    isq = typ & 1 ? 3 : 5;
    A = typ & 1 ? cp(3, 1) / cp(6, 0) : cp(1, 0) / cp(0, 1);
    B = typ & 1 ? cp(3, - 1) / cp(6, 0) : cp(- 1, 0) / cp(0, 1);
    x = typ & 1 ? cp(2, 1) : cp(1, 1) / cp(2, 0);
    y = typ & 1 ? cp(2, - 1) : cp(1, - 1) / cp(2, 0);
}

signed main(){
    prework(); int T = rd(), typ = rd(); init(typ);
    while(T--){
        ll l = rd(), r = rd(), len = r - l + 1; int k = rd(); cp res;
        if(typ & 1)l = (l + 1) / 2, r /= 2; else ++l, ++r;
        for(int i = 0; i <= k; ++i){
            cp tmp;
            for(int j = 0; j <= i; ++j){
                cp t = C[i][j] * (A ^ j) * (B ^ (i - j)) * F((x ^ j) * (y ^ (i - j)), l, r);
                tmp = tmp + t;
            }
            tmp = tmp * s1[k][i];
            res = (k - i & 1 ? res - tmp : res + tmp);
        }
        cout << (res / cp(len, 0) * ifa[k]).a << endl;
    }
    return 0;
}