U559662 不一般的操作-区间dp

U559662 不一般的操作

解析

对于操作次数只有 \(0\) 次的答案，直接判断 \(p\) 数组是否是 \(1\) 到 \(n\) 即可。

对于操作次数只有 \(1\) 次的答案，枚举断点 \(k\) ，此时的话，拆分为两个数组后，只需要判断两个数组是否都是给定的 \(p\) 数组的子序列。

对于 \(100 \%\) 的数据范围，思考整个过程是不是一直枚举断点即可，枚举 \(k\) 次？？？

比如给出一个数据

4 2
5 1
2 1 3 4

实际上，我们可以获悉，为了贡献值最小，可能按照其他方式先排其他位置

[1, 2, 3, 4] 变成 [2, 1, 3, 4]
可以设置断点就是k = 3
[1, 2, 3, 4]拆分为[1]和[2, 3, 4]
然后一次插入就可以搞定，1 放在 2 和 3 的中间
花费是3 * 5 = 15

还可以
第一次操作
    [1, 2, 3, 4] 变成 [1, 3, 2, 4]
    设置断点k = 2
    [1, 2, 3, 4]拆分为[1, 2]和[ 3, 4]
    合并为[1, 3, 2, 4]
第二次操作
    [1, 3, 2, 4]变成[2, 1, 3, 4]
    设置断点k = 2
    [1, 3, 2, 4]拆分为[1, 3]和[2, 4]
    合并为[2, 1, 3, 4]
花费是2 * 5 + 2 * 1 = 12

正向考虑会存在一个不确定性，即使可以获悉最终答案，但是时间仍然非常大。

遇到类似的题，关键要点在于正向考虑过于复杂，反向思考整个过程如何逆序？？

比如正向考虑，划分一个断点，然后进行归并

反向考虑，选取一个子序列，放入到末尾，最终目标是让数组升序。

如果反向想变成 [1,2,3,4]，则说明一定可以找到子序列[1,k]另外剩余的数字也是一个子序列，是[k + 1, 4]

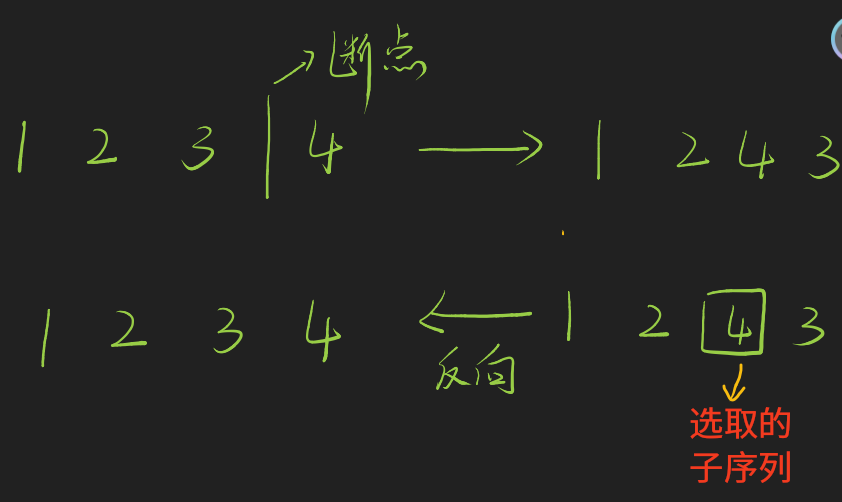
关键点我们可以这样理解：

反向操作实际上就是从右侧序列之中找出两段数字连续上升的子序列，合并为一段数字连续上升，其他值保持不变

比如上图右侧的 \([1, 2, 3]\) 就是其中的数字连续上升的子序列， 其中的 \([4]\) 也是数字连续上升的子序列。

其实我们会发现一个最终问题，如果想把上述序列 \([1, 2, 3, 4]\) 排好序

可能是以下三种情况之一：

子序列 \([1, 2, 3,4]\) 和 子序列 \([]\) 反向合并，右侧找不到子序列 \([]\) ，所以此种合并失败，此时的断点就是 \(k = 0\) 。

子序列 \([1, 2, 3]\) 和 子序列 \([4]\) 反向合并，右侧这两个子序列都存在，合并成功，此时的断点就是 \(k = 1\) 。

子序列 \([1, 2]\) 和 子序列 \([3,4]\) 反向合并，很明显右侧找不出子序列 \([3, 4]\)，所以此种合并失败，此时的断点就是 \(k = 2\) 。

子序列 \([1]\) 和 子序列 \([2,3,4]\) 反向合并，很明显右侧找不出子序列 \([2, 3, 4]\)，所以此种合并失败，此时的断点就是 \(k = 3\) 。

子序列 \([]\) 和 子序列 \([1，2，3，4]\) 反向合并，很明显右侧找不到子序列 \([1，2，3，4]\) ，所以此种合并失败，此时的断点是 \(k = 4\) 。

所以现在反向问题转移到，是否右侧存在子序列 \([1, n - k]\) 以及子序列 \([n - k + 1, n]\) ， 只要存在，就可以满足合法条件，继续往右侧的右侧继续询问，

对于子序列 \([1, n - k]\) ，又可以继续划分，看其右侧的右侧是否可以找到这样的两个子序列。

比如能找到子序列 \([1, 2]\) 和 子序列 \([3]\) ，肯定可以合并为子序列 \([1, 2, 3]\)

现在按照这组数据进行举例

4 2
5 1
2 1 3 4

① 确定状态
dp[x][l][r] 表示数值在[l, r]之内的数字，通过第x次到第t次操作内已经排好序的最小代价
② 确定答案
dp[1][1][n]
③ 确定状态转移方程
// 前面所有操作之中，结合划分为两个非空子段之后，尝试是否存在最小值
dp[x][i][j] = min(dp[x + 1][i][j], dp[x + 1][i][k] + dp[x + 1][k + 1][j] + (j - k) * c[x]);
④ 确定初始值和边界条件
dp[t + 1][i][i] = 0; // p[i]这个点排好序不需要满足任何条件
dp[t + 1][i][j] = 0
满足i到j是单调上升的

最终实现的时间复杂度 \(O(t \times n ^ 3)\) 。

最终可能需要注意到的是，本题可以理解为反向选取两个子序列然后拼接的方式

最坏情况下，最后答案之中一个上升的连续的子序列，比如[1], [1,2],[1,2,3,4]都不存在，

此时一定是 \([n, n - 1 \dots 1]\) 的输入。

另外只要 \(t\) 给的足够大，慢慢逆向也一定可以得到原来的递增数组。