计算几何--判断两条线段相交--poj 2653

Pick-up sticks

Time Limit: 3000MS		Memory Limit: 65536K
Total Submissions: 8862		Accepted: 3262

Description

Stan has n sticks of various length. He throws them one at a time on the floor in a random way. After finishing throwing, Stan tries to find the top sticks, that is these sticks such that there is no stick on top of them. Stan has noticed that the last thrown
stick is always on top but he wants to know all the sticks that are on top. Stan sticks are very, very thin such that their thickness can be neglected.

Input

Input consists of a number of cases. The data for each case start with 1 <= n <= 100000, the number of sticks for this case. The following n lines contain four numbers each, these numbers are the planar coordinates of the endpoints of one stick. The sticks
are listed in the order in which Stan has thrown them. You may assume that there are no more than 1000 top sticks. The input is ended by the case with n=0. This case should not be processed.

Output

For each input case, print one line of output listing the top sticks in the format given in the sample. The top sticks should be listed in order in which they were thrown. 



The picture to the right below illustrates the first case from input.

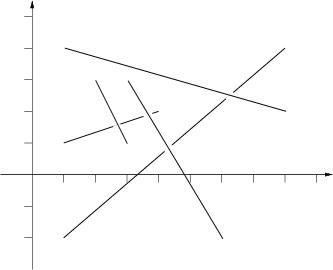
Sample Input

5
1 1 4 2
2 3 3 1
1 -2.0 8 4
1 4 8 2
3 3 6 -2.0
3
0 0 1 1
1 0 2 1
2 0 3 1
0

Sample Output

Top sticks: 2, 4, 5.
Top sticks: 1, 2, 3.

Hint

Huge input,scanf is recommended.

Source

Waterloo local 2005.09.17

题意：

          依次给出n条线段，后添的线段若与先前的线段相交，则会覆盖先前的线段，问最后会有多少天线段，输出所能看见线段的下标。。。。。

          判断两条线段相交

思路：

         判断线段AB与线段CD是否相交；

         1：以线段AB，线段CD为对角线所构成的矩形相交，则继续判断；(用以排除两线段同线但不相交的情况)

         2：用叉积运算判断点A，B是否在线段CD两侧，判断点C，D是否在线段AB两侧，若符合，则两先段相交！

代码：

#include "cstdio"
#include "cmath"
#include "vector"
#include "iostream"

using namespace std;
const double eps = 1e-8;

double max(double a,double b){ return a>b?a:b; }
double min(double a,double b){ return a<b?a:b; }

int cmp(double x){
    if(fabs(x)<eps) return 0;
    if(x>0) return 1;
    return -1;
}

inline double sqr(double x){
    return x*x;
}

struct point{   //点结构体
    double x,y;
    point(){}
    point (double a,double b):x(a),y(b) {} //重载
    void input(){
        scanf("%lf%lf",&x,&y);
    }
    friend point operator + (const point a,const point b){
        return point(a.x+b.x,a.y+b.y);
    }
    friend point operator - (const point a,const point b){
        return point(a.x-b.x,a.y-b.y);
    }
};

double det(const point &a,const point &b){   //向量a与向量b的叉积
    return a.x*b.y-a.y*b.x;
}

struct line{   //线结构体
    point a,b;
    line(){}
    line(point x,point y):a(x),b(y){}
};

bool line_make_point_one(line a,line b){   //判断两线段是否相交，完美代码！
    return
        max(a.a.x,a.b.x) >= min(b.a.x,b.b.x) &&  //前四行判断两向量所形成的矩形是否相交，排除两线段在同一条直线但不相交的可能
        max(b.a.x,b.b.x) >= min(a.a.x,a.b.x) &&
        max(a.a.y,a.b.y) >= min(b.a.y,b.b.y) &&
        max(b.a.y,b.b.y) >= min(a.a.y,a.b.y) &&
        cmp(det(a.a-b.b,b.a-b.b))*cmp(det(a.b-b.b,b.a-b.b))<=0 &&  //判断两线段是否相交
        cmp(det(b.a-a.a,a.b-a.a))*cmp(det(b.b-a.a,a.b-a.a))<=0;
}

int main(){
    int n;
    while(scanf("%d",&n),n!=0)
    {
        line a;
        vector<line> p;  //线段向量
        vector<int> v;  //记录线段向量的下标
        p.clear();
        v.clear();

        scanf("%lf %lf %lf %lf",&a.a.x,&a.a.y,&a.b.x,&a.b.y);
        p.push_back(a);
        v.push_back(1);
        for(int k=2;k<=n;++k)
        {
            scanf("%lf %lf %lf %lf",&a.a.x,&a.a.y,&a.b.x,&a.b.y);
            for(int i=0; i<(int)p.size(); ++i)
            {
                bool flag = line_make_point_one(a,p[i]);
                if(flag==true)
                {
                    p.erase(p.begin()+i);
                    v.erase(v.begin()+i);
                    i--;
                }
            }
            p.push_back(a);
            v.push_back(k);
        }
        printf("Top sticks:");
        int i;
        for( i=0; i<(int)v.size()-1; ++i)
            printf(" %d,",v[i]);
        printf(" %d.\n",v[i]);
    }
    return 0;
}