最大权闭合图 && 【BZOJ】1497: [NOI2006]最大获利

http://www.lydsy.com/JudgeOnline/problem.php?id=1497

最大权闭合图详细请看胡伯涛论文《最小割模型在信息学竞赛中的应用》，我在这里截图它的定义以及一些东西。

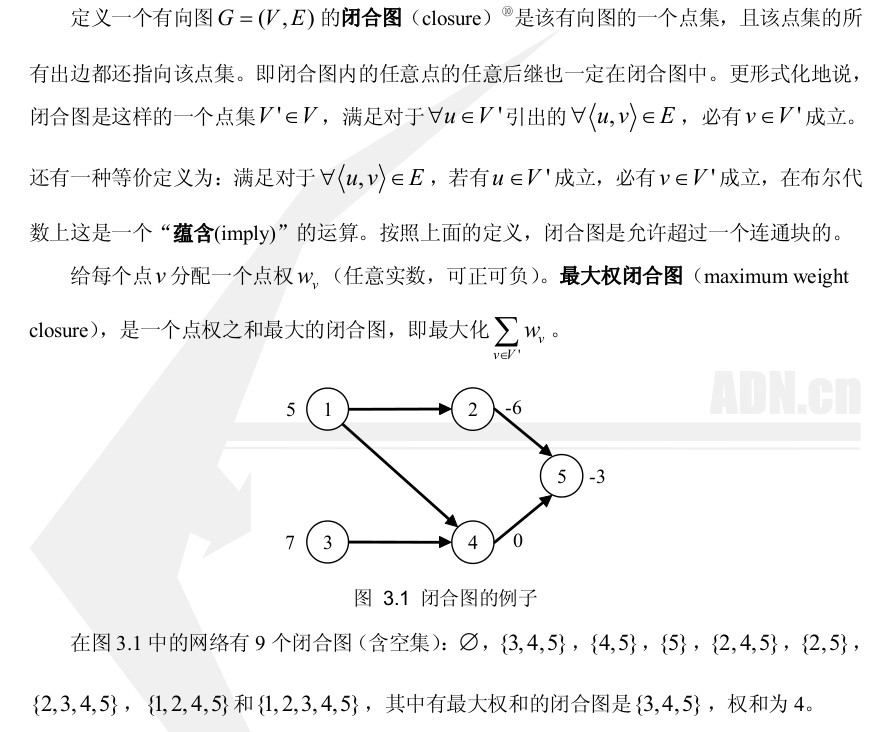
假设我们有一个图，点集的出边都是连到点集的，那么称这个为闭合图。现在这些点集都有个权值，我们要选择某个闭合图使得权值最大。

回到此题：

最大获利这一题，我们可以这样看，用户群和中转站为带权的点集，用户群的权为收益，中转站的权为负的成本，即0-成本，用户群向其中两个中转站连弧，那么这个就是一个闭合图。

我们要求这个闭合图的权值和最大，即最大收益，那么就能转移到上面的求最大权闭合图的做法去了。

做法就是：

从源s连弧到正权值的点，容量为次正权值。
从负权值的点连弧到汇t，容量为负权值的绝对值。
在闭合图中所有的弧换成容量为oo的弧。
答案就是所有正权值的和-最小割的容量（最大流）

那么此题就解决了。

（注意范围啊。，。。我又RE了一次，，好多次都是数组开小了啊>A<。）

#include <cstdio>

using namespace std;

const int N=60000, M=350000, oo=1000000000;

#define min(a,b) ((a)<(b)?(a):(b))

int ihead[N], inext[M], from[M], to[M], cap[M], cnt=1;

int cur[N], gap[N], d[N], p[N];

int isap(int s, int t, int n) {

	int i, maxflow=0, f, u;

	for(i=0; i<=n; ++i) cur[i]=ihead[i];

	gap[0]=n; u=s;

	while(d[s]<n) {

		for(i=cur[u]; i; i=inext[i]) if(d[to[i]]+1==d[u] && cap[i]) break;

		if(i) {

			cur[u]=i; p[to[i]]=i; u=to[i];

			if(u==t) {

				for(f=oo; u!=s; u=from[p[u]]) f=min(f, cap[p[u]]);

				for(u=t; u!=s; u=from[p[u]]) cap[p[u]]-=f, cap[p[u]^1]+=f;

				maxflow+=f;

			}

		}

		else {

			if(!(--gap[d[u]])) break;

			d[u]=n;

			for(i=ihead[u]; i; i=inext[i]) if(cap[i] && d[u]>d[to[i]]+1)

				d[u]=d[to[i]]+1, cur[u]=i;

			++gap[d[u]]; if(u!=s) u=from[p[u]];

		}

	}

	return maxflow;

}

void add(int u, int v, int c) {

	inext[++cnt]=ihead[u]; ihead[u]=cnt; from[cnt]=u; to[cnt]=v; cap[cnt]=c;

	inext[++cnt]=ihead[v]; ihead[v]=cnt; from[cnt]=v; to[cnt]=u; cap[cnt]=0;

}

int main() {

	int n, m, sum=0;

	scanf("%d%d", &n, &m);

	int i, a, b, c;

	for(i=1; i<=n; ++i) {

		scanf("%d", &c);

		add(m+i, n+m+1, c);

	}

	for(i=1; i<=m; ++i) {

		scanf("%d%d%d", &a, &b, &c);

		sum+=c;

		add(i, m+a, oo); add(i, m+b, oo);

		add(0, i, c);

	}

	printf("%d\n", sum-isap(0, n+m+1, n+m+2));

	return 0;

}

Description

新的技术正冲击着手机通讯市场，对于各大运营商来说，这既是机遇，更是挑战。THU集团旗下的CS&T通讯公司在新一代通讯技术血战的前夜，需要做太多的准备工作，仅就站址选择一项，就需要完成前期市场研究、站址勘测、最优化等项目。在前期市场调查和站址勘测之后，公司得到了一共N个可以作为通讯信号中转站的地址，而由于这些地址的地理位置差异，在不同的地方建造通讯中转站需要投入的成本也是不一样的，所幸在前期调查之后这些都是已知数据：建立第i个通讯中转站需要的成本为Pi（1≤i≤N）。另外公司调查得出了所有期望中的用户群，一共M个。关于第i个用户群的信息概括为Ai, Bi和Ci：这些用户会使用中转站Ai和中转站Bi进行通讯，公司可以获益Ci。（1≤i≤M, 1≤Ai, Bi≤N） THU集团的CS&T公司可以有选择的建立一些中转站（投入成本），为一些用户提供服务并获得收益（获益之和）。那么如何选择最终建立的中转站才能让公司的净获利最大呢？（净获利 = 获益之和 - 投入成本之和）

Input

输入文件中第一行有两个正整数N和M 。第二行中有N个整数描述每一个通讯中转站的建立成本，依次为P1, P2, …, PN 。以下M行，第(i + 2)行的三个数Ai, Bi和Ci描述第i个用户群的信息。所有变量的含义可以参见题目描述。

Output

你的程序只要向输出文件输出一个整数，表示公司可以得到的最大净获利。

Sample Input

5 5
1 2 3 4 5
1 2 3
2 3 4
1 3 3
1 4 2
4 5 3

Sample Output

HINT

【样例说明】选择建立1、2、3号中转站，则需要投入成本6，获利为10，因此得
到最大收益4。【评分方法】本题没有部分分，你的程序的输出只有和我们的答案完全一致才能获得满分，否则不得分。【数据规模和约定】
80%的数据中：N≤200，M≤1 000。 100%的数据中：N≤5 000，M≤50 000，0≤Ci≤100，0≤Pi≤100。

Source

网络流