数据结构Java实现06----中缀表达式转换为后缀表达式

本文主要内容：

• 表达式的三种形式
• 中缀表达式与后缀表达式转换算法

一、表达式的三种形式：

• 中缀表达式：运算符放在两个运算对象中间，如：(2+1)*3。我们从小做数学题时，一直使用的就是中缀表达式。
• 后缀表达式：不包含括号，运算符放在两个运算对象的后面，所有的计算按运算符出现的顺序，严格从左向右进行（不再考虑运算符的优先规则），如：2 1 + 3 *。又比如3+(6-4/2)*5=23的后缀表达式为：3642/-5*+# (#符号为结束符)
• 前缀表达式：同后缀表达式一样，不包含括号，运算符放在两个运算对象的前面，如：* + 2 1 3 。前缀表达式和后缀表达式其实是差不多的，只不过符号位置不同而已，前缀表达式不是很常见。

二、中缀表达式转换为后缀表达式：（思路）

1、将中缀表达式转换为后缀表达式：（步骤，有点难理解）

(1)当读到数字直接送至输出队列中；

(2)当读到运算符t时：

　　a.将栈中所有优先级高于或等于t的运算符弹出，送到输出队列中；

　　　　注：这句话不好理解，可以说成这样，从栈顶开始，依次弹出比当前处理的运算符优先级高的运算符，直到一个比它优先级低的或者遇到了一个左括号就停止。

　　b.t进栈；

（3）读到左括号时总是将它压入栈中；

（4）读到右括号时，将靠近栈顶的第一个左括号上面的运算符全部依次弹出，送至输出队列后，再丢弃左括号；

（5）中缀表达式全部读完后，若栈中仍有运算符，将其送到输出队列中。

 

举例：

上图中，左侧的那一列为输出序列，右侧的那一列为栈。

2、运用后缀表达式进行计算：

　　(1)建立一个栈S；

　　(2)从左到右读后缀表达式，读到数字就将它转换为数值压入栈S中，读到运算符则从栈中依次弹出两个数分别到Y和X，然后以“X 运算符 Y”的形式计算机出结果，再压加栈S中；

　　(3)如果后缀表达式未读完，就重复上面过程，最后输出栈顶的数值则为结束。

举例：

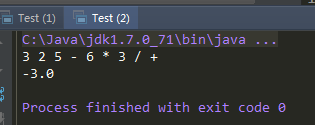
3+(2-5)*6/3=-3 ,其后缀表达式为：325-6*3/+。其运算结果如下：

三、代码实现：将中缀表达式转换为后缀表达式

• JDK  Stack类使用
• 使用泛型

代码实现：

(1)StringToArithmetic.java:（中缀表达式转化为后缀表达式的工具类）

 /**
  * Created by smyhvae on 2015/9/7.
  * 工具类：
  * 1、中缀表达式转化为后缀表达式
  * 2、给出一个算术表达式（中缀表达式），直接得到计算结果
  */

 import java.util.Stack;
 import java.util.regex.Pattern;

 public class StringToArithmetic {

     private StringToArithmetic() {
     }

     //方法：给出一个算术表达式（中缀表达式），得到计算结果。 例如 (5+8+10)*1，返回23
     public static double stringToArithmetic(String string) {
         return suffixToArithmetic(infixToSuffix(string));
     }

     /**
      * 中缀表达式转后缀表达式 只处理了+,-,*,/和括号，没有处理负号及其它运算符，也没对前缀表达式验证。
      * 如要处理负号，可对表达式进行预转义处理，当下面条件成立时，将负号换成单目运算符"!" infix.charAt[i]=='-'&&(
      * i==0||infix.charAt[i-1]=='(')
      * 3*6/4+3
      * 3+6-4           3 6 + 4 -
      * 3+(6-4/2)*5    3 6 4 2 / - 5 * +
      */
     //方法：中缀表达式转成后缀表达式
     public static String infixToSuffix(String infix) {
         Stack<Character> stack = new Stack<Character>();
         String suffix = "";
         int length = infix.length();
         for (int i = 0; i < length; i++) {
             Character temp;
             char c = infix.charAt(i);
             switch (c) {
                 // 忽略空格
                 case ' ':
                     break;
                 // 碰到'('，push到栈
                 case '(':
                     stack.push(c);
                     break;
                 // 碰到'+''-'，将栈中所有运算符弹出，送到输出队列中
                 case '+':
                 case '-':
                     while (stack.size() != 0) {
                         temp = stack.pop();
                         if (temp == '(') {
                             stack.push('(');
                             break;
                         }
                         suffix += " " + temp;
                     }
                     stack.push(c);
                     suffix += " ";
                     break;
                 // 碰到'*''/'，将栈中所有乘除运算符弹出，送到输出队列中
                 case '*':
                 case '/':
                     while (stack.size() != 0) {
                         temp = stack.pop();
                         if (temp == '(' || temp == '+' || temp == '-') {
                             stack.push(temp);
                             break;
                         } else {
                             suffix += " " + temp;
                         }
                     }
                     stack.push(c);
                     suffix += " ";
                     break;
                 // 碰到右括号，将靠近栈顶的第一个左括号上面的运算符全部依次弹出，送至输出队列后，再丢弃左括号
                 case ')':
                     while (stack.size() != 0) {
                         temp = stack.pop();
                         if (temp == '(')
                             break;
                         else
                             suffix += " " + temp;
                     }
                     // suffix += " ";
                     break;
                 //如果是数字，直接送至输出序列
                 default:
                     suffix += c;
             }
         }

         //如果栈不为空，把剩余的运算符依次弹出，送至输出序列。
         while (stack.size() != 0) {
             suffix += " " + stack.pop();
         }
         return suffix;
     }

     /**
      * postfix
      *
      * @return double
      */
     //方法：通过后缀表达式求出算术结果
     public static double suffixToArithmetic(String postfix) {

         Pattern pattern = Pattern.compile("\\d+||(\\d+\\.\\d+)"); //使用正则表达式 匹配数字
         String strings[] = postfix.split(" ");  //将字符串转化为字符串数组
         for (int i = 0; i < strings.length; i++)
             strings[i].trim();  //去掉字符串首尾的空格
         Stack<Double> stack = new Stack<Double>();

         for (int i = 0; i < strings.length; i++) {

             if (strings[i].equals(""))
                 continue;

             //如果是数字，则进栈
             if ((pattern.matcher(strings[i])).matches()) {

                 stack.push(Double.parseDouble(strings[i]));
             } else {
                 //如果是运算符，弹出运算数，计算结果。
                 double y = stack.pop();
                 double x = stack.pop();
                 stack.push(caculate(x, y, strings[i])); //将运算结果重新压入栈。
             }
         }
         return stack.pop(); //弹出栈顶元素就是运算最终结果。

     }

     private static double caculate(double x, double y, String simble) {
         if (simble.trim().equals("+"))
             return x + y;
         if (simble.trim().equals("-"))
             return x - y;
         if (simble.trim().equals("*"))
             return x * y;
         if (simble.trim().equals("/"))
             return x / y;
         return 0;
     }
 }

(2)Test.java:(测试类)

 public class Test {
     public static void main(String[] args) {

         String str = "3+(2-5)*6/3";  //其后缀表达式为325-6*3/+

         //调用方法：中缀表达式转成后缀表达式
         System.out.println(StringToArithmetic.infixToSuffix(str));

         //调用方法：给出一个算术表达式（中缀表达式），得到计算结果
         System.out.println(StringToArithmetic.stringToArithmetic(str));

     }

 }

上方代码中，第07行是根据中缀表达式算出后缀表达式。

第10行：是给出一个中缀表达式，直接的到计算结果，其实它的步骤是：先根据中缀表达式得到后缀表达式，然后根据后缀表达式去计算结果。

运行效果：