Codeforces 1045E. Ancient civilizations 构造 计算几何 凸包

原文链接https://www.cnblogs.com/zhouzhendong/p/CF1045E.html

4K码量构造题，CF血腥残暴！

题解

首先，如果所有点颜色相同，那么直接连个菊花搞定。

然后我们建个凸包。

如果凸包上有大于2段颜色（就是至少四段），比如这样

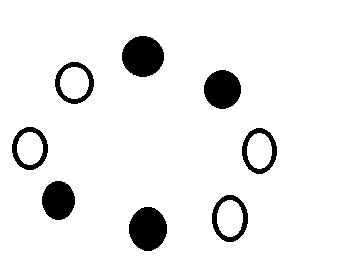
那么必然无解。

否则就只有一段颜色或者两段颜色：

这里我们先不管这个，考虑一个三角形的构造。

考虑三角形三个顶点颜色不全相同的情况，例如：

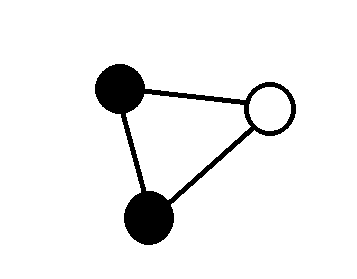
（两个白点的情况是等价的）

假如三角形区域内没有白点，那么直接全部连到其中一个黑点就好了。

否则假设里面有一个白点：

那么我们将白顶点连上这个中间的白点（将红色边加入最终答案），把原三角形划分成3个子问题递归求解即可。

回到原问题：

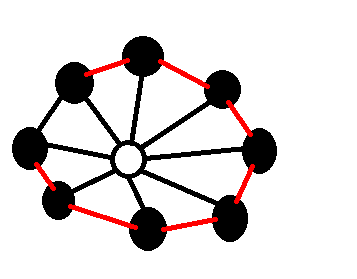
如果凸包上只有一种颜色，那么在里面找一个白点（因为已经排除全部都是黑点的情况了，所以必然有白点），如下图一样将红色边相连，按照红/黑色边将凸包三角划分成子问题解决即可：

如果凸包上有两种颜色，那么就类似地：

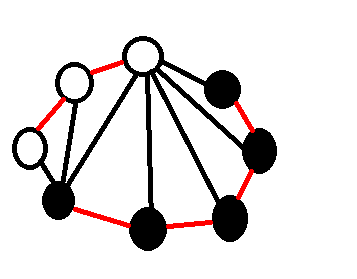
划分集合的暴力枚举点判定是否在三角形内就好了。

代码

#include <bits/stdc++.h>
#define clr(x) memset(x,0,sizeof (x))
using namespace std;
typedef long long LL;
LL read(){
	LL x=0,f=0;
	char ch=getchar();
	while (!isdigit(ch))
		f|=ch=='-',ch=getchar();
	while (isdigit(ch))
		x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
	return f?-x:x;
}
const int N=1005;
int n;
struct Point{
	int x,y;
	Point(){}
	Point(int _x,int _y){
		x=_x,y=_y;
	}
	friend Point operator + (Point A,Point B){
		return Point(A.x+B.x,A.y+B.y);
	}
	friend Point operator - (Point A,Point B){
		return Point(A.x-B.x,A.y-B.y);
	}
	friend bool operator == (Point A,Point B){
		return A.x==B.x&&A.y==B.y;
	}
	friend bool operator != (Point A,Point B){
		return A.x!=B.x||A.y!=B.y;
	}
}O;
int cross(Point A,Point B){
	return A.x*B.y-B.x*A.y;
}
int cross(Point A,Point B,Point C){
	return cross(B-A,C-A);
}
int Dot(Point A,Point B){
	return A.x*B.x+A.y*B.y;
}
int Dis(Point A,Point B){
	return Dot(A-B,A-B);
}
struct civ{
	Point p;
	int c,id;
	civ(){}
	civ(Point _p,int _c,int _id){
		p=_p,c=_c,id=_id;
	}
};
civ Get_civ(int id){
	Point p;
	p.x=read(),p.y=read();
	int c=read();
	return civ(p,c,id);
}
vector <civ> p,con;
bool cmpO(Point a,Point b){
	return a.y!=b.y?a.y<b.y:a.x<b.x;
}
bool cmpAngle_civ(civ a,civ b){
	int c=cross(O,a.p,b.p);
	return c?c>0:Dis(O,a.p)<Dis(O,b.p);
}
vector <civ> Get_Convex(vector <civ> p){
	vector <civ> st(0);
	int n=p.size();
	for (int i=1;i<n;i++)
		if (!cmpO(p[0].p,p[i].p))
			swap(p[0],p[i]);
	O=p[0].p;
	sort(p.begin()+1,p.end(),cmpAngle_civ);
	for (int i=0;i<n;i++){
		while (st.size()>1&&cross(st[st.size()-2].p,st.back().p,p[i].p)<=0)
			st.pop_back();
		st.push_back(p[i]);
	}
	return st;
}
int check_same(){
	for (int i=1;i<n;i++)
		if (p[i].c!=p[0].c)
			return 0;
	return 1;
}
int check_inside(Point A,Point B,Point C,Point P){
	if (P==A||P==B||P==C)
		return 0;
	int S1=abs(cross(A,B,C));
	int S2=abs(cross(P,A,B))+abs(cross(P,B,C))+abs(cross(P,C,A));
	return S1==S2;
}
vector <civ> get_inside(Point A,Point B,Point C,vector <civ> S){
	static vector <civ> res;
	res.clear();
	for (auto v : S)
		if (check_inside(A,B,C,v.p))
			res.push_back(v);
	return res;
}
vector <pair <int,int> > ans;
void solve(civ A,civ B,civ C,vector <civ> S){
	int flag=0;
	civ p;
	for (auto c : S)
		if (c.c!=A.c){
			flag=1,p=c;
			break;
		}
	if (!flag){
		for (auto c : S)
			ans.push_back(make_pair(A.id,c.id));
		return;
	}
	ans.push_back(make_pair(C.id,p.id));
	solve(A,B,p,get_inside(A.p,B.p,p.p,S));
	solve(C,p,A,get_inside(C.p,p.p,A.p,S));
	solve(C,p,B,get_inside(C.p,p.p,B.p,S));
}
int main(){
	n=read();
	for (int i=1;i<=n;i++)
		p.push_back(Get_civ(i));
	con=Get_Convex(p);
	int cnt=con[0].c^con.back().c;
	for (int i=1;i<con.size();i++)
		cnt+=con[i-1].c^con[i].c;
	if (cnt>2)
		return puts("Impossible"),0;
	ans.clear();
	if (cnt==0){
		if (check_same()){
			printf("%d\n",n-1);
			for (int i=1;i<n;i++)
				printf("%d %d\n",0,i);
			return 0;
		}
		for (int i=1;i<con.size();i++)
			ans.push_back(make_pair(con[i-1].id,con[i].id));
		civ mid;
		for (auto c : p)
			if (c.c!=con[0].c){
				mid=c;
				break;
			}
		solve(con[0],con.back(),mid,get_inside(con[0].p,con.back().p,mid.p,p));
		for (int i=1;i<con.size();i++)
			solve(con[i-1],con[i],mid,get_inside(con[i-1].p,con[i].p,mid.p,p));
	}
	else {
		vector <civ> _con(0);
		int stco=con[0].c^1,i;
		int m=con.size();
		for (i=0;;i=(i+1)%m)
			if (con[i].c==stco){
				_con.push_back(con[i]);
				if (con[(i+1)%m].c!=stco)
					break;
			}
		stco^=1;
		for (i=(i+1)%m;;i=(i+1)%m)
			if (con[i].c==stco){
				_con.push_back(con[i]);
				if (con[(i+1)%m].c!=stco)
					break;
			}
		con=_con;
		for (i=0;i<m;i++)
			if (con[i].c!=con[(i+1)%m].c)
				break;
		int b=i;
		for (int i=0;i<b;i++)
			ans.push_back(make_pair(con[i].id,con[i+1].id));
		for (int i=b+1;i<m-1;i++)
			ans.push_back(make_pair(con[i].id,con[i+1].id));
		b++;
		for (int i=0;i<b-1;i++)
			solve(con[i],con[i+1],con[b],get_inside(con[i].p,con[i+1].p,con[b].p,p));
		for (int i=b;i<m-1;i++)
			solve(con[i],con[i+1],con[0],get_inside(con[i].p,con[i+1].p,con[0].p,p));
	}
	printf("%d\n",(int)ans.size());
	for (auto e : ans)
		printf("%d %d\n",e.first-1,e.second-1);
	return 0;
}