【LeetCode每天一题】Unique Paths(唯一的路径数)

A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below).  How many possible unique paths are there?

Note: m and n will be at most 100.

Example 1:

Input: m = 3, n = 2
Output: 3
Explanation:
From the top-left corner, there are a total of 3 ways to reach the bottom-right corner:
1. Right -> Right -> Down
2. Right -> Down -> Right
3. Down -> Right -> Right

Example 2:

Input: m = 7, n = 3
Output: 28

思路

---

　　在求路径数这一方面的问题时，第一想到的就是回溯法求解。因为每次只能左移动和下移动，因此移动之后判断以下是否超出运动范围，然后再继续向左或向下移动。使用一个变量来记录路径数。
　　使用回溯法写完之后发现运行时间超时了，那就说明回溯法不是这道题的最优解，因此我们可以使用动态规划来解决，我们申请一个辅助矩阵，然后值都初始化为1， 行和列都是从1开始开始计数，动态方程为dp[i][j] = dp[i-1][j] + dp[i][j-1] 。一直到矩阵的最后一个元素。而该元素的值就是结果数。
　　另外因此根据这个动态方程我们可以发现每次只用到了上一行同位置的元素和同行中前一个位置的元素。根据这个特点我们可以设置一个长度和列长相等的辅助数据，然后动态方程为dp[j] += dp[j-1]。循环row次，最终数组中最后一个元素的值就为结果。时间复杂度为O(row*cloum), 空间复杂度为O(cloum)。
动态规划的图示步骤

---

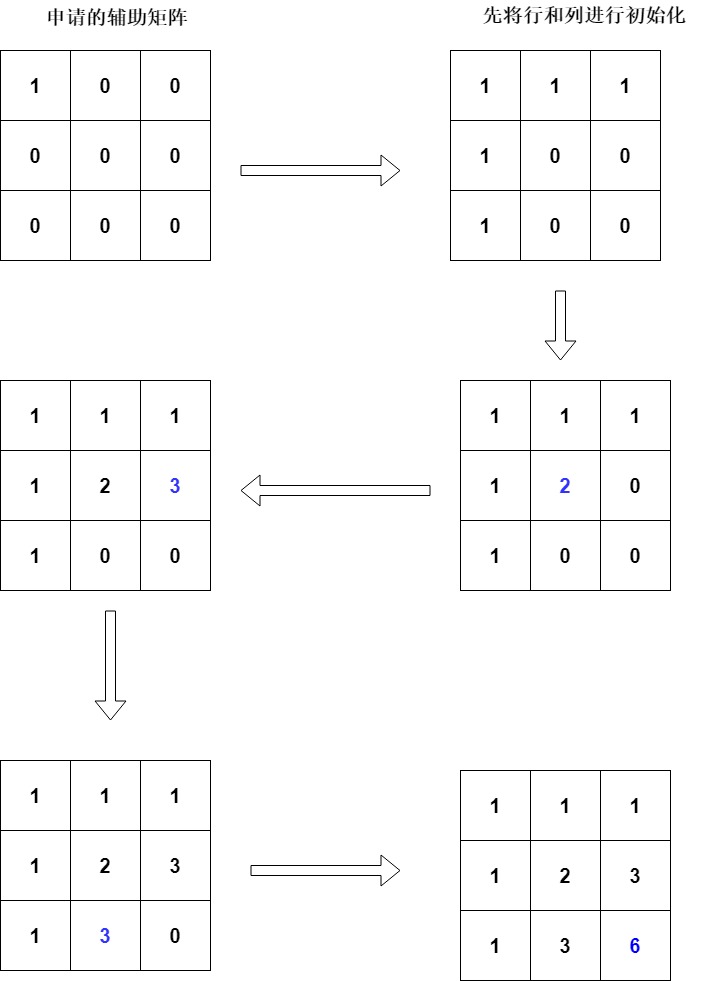
解决代码

---

    回溯法

 class Solution(object):
     def uniquePaths(self, m, n):
         """
         :type m: int
         :type n: int
         :rtype: int
         """         count = [0]        # 记录结果数
         self.Backtracking(m-1, n-1, 0, 0, count)
         return count[0]      # 返回结果

     def Backtracking(self, m, n,row, cloum, count):        # 回溯函数
         if row == m and cloum == n:             # 达到右下角，增加数量
             count[0] += 1
             return
         if row > m or cloum > n:             # 越界直接返回
             return
         if row != m:                           # 等于m的时候不能向下走
             self.Backtracking(m, n, row+1, cloum, count)
         if cloum != n:                        # 等于n的时候不能向右走。
             self.Backtracking(m, n, row, cloum+1, count)

　　动态规划(第一种办法)

 class Solution(object):
     def uniquePaths(self, m, n):
         """
         :type m: int
         :type n: int
         :rtype: int
         """
         dp = []
         for i in range(m):          # 申请一个m*n的矩阵，并将值初始化为1
             dp.append([1]*n)

         for i in range(1, m):         # 从1开始遍历，得到每一个位置的路径树
             for j in range(1, n):
                 dp[i][j] = dp[i-1][j] + dp[i][j-1]

         return dp[m-1][n-1]       # 最终结果
         

　　动态规划第二种思路

 class Solution(object):
     def uniquePaths(self, m, n):
         """
         :type m: int
         :type n: int
         :rtype: int
         """         dp = [1]*n            # 申请长度为n的数组
         for i in range(1, m):       # 遍历m行，每行n个位置
             for j in range(1,n):
                     dp[j] += dp[j-1] 

         return dp[-1]  返回结果