week01-绪论

一.作业题目

仿照三元组或复数的抽象数据类型写出有理数抽象数据类型的描述 （有理数是其分子、分母均为整数且分母不为零的分数）。
           有理数基本运算：

1. 构造有理数T，元素e1,e2分别被赋以分子、分母值
2. 销毁有理数T
3. 用e(引用类型参数)返回有理数T的分子或分母,当入参i为1时返回分子, i为2是返回分母。
4. 将有理数T的分子或分母更改为e,入参i为1时改变分子, i为2是改变分母
5. 有理数T1,T2相加,结果存入有理数T3
6. 有理数T1,T2相减,结果存入有理数T3
7. 有理数T1,T2相乘,结果存入有理数T3
8. 有理数T1,T2相除,结果存入有理数T3
   实验要求：
9. 抽象数据类型名为Rational。
10. 有理数分母不能为负数或者0，类似输入请提示重输入。
11. 数据对象和数据运算的表示与数据操作的实现分离。表示用头文件完成，实现用CPP文件完成。Main.cpp文件实现数据输入输出。
12. 数据输入输出格式参考如下：
    输入：
    1 3 //T1的分子、分母
    1 2 //T2的分子、分母
    ** 输出：**
        5 6  //两个有理数相加
        -1 6  //两个有理数相减
         1 6  //两个有理数相乘
         2 3  //两个有理数相除

程序应对异常输入或者出错必要处理和提示，比如提示：“分数是否需要约分等”。

二.作业内容

1、用ADT的抽象数据模型描述你的有理数数据类型

    ADT Rational-Num{

数据对象：D = {T1,T2,T3|T1,T2,T3为有理数}
数据关系：R = {<T1,T2>,<T2,T3>}
基本操作：
InitTriplet(Triplet &T, ElemType v1, ElemType v2)
操作结果：构造一个有理数T，其分子和分母分别为e1和e2
DestroyTriplet(Triplet &T)
操作结果：销毁有理数T
Get(Triplet T, int i, ElemType &e)
操作结果：用e返回有理数T的分子或分母,i为1时返回分子, i为2是返回分母
Put(Triplet &T, int i, ElemType e)
操作结果：将有理数T的分子或分母更改为e,i为1时改变分子, i为2是改变分母
Add(Triplet &T1,Triplet &T2,Triplet &T3)
操作结果：将T1，T2相加，结果存入T3
Sub(Triplet &T1,Triplet &T2,Triplet &T3)
操作结果：将T1，T2相减，结果存入T3
Mul(Triplet &T1,Triplet &T2,Triplet &T3)
操作结果：将T1，T2相乘，结果存入T3
Div(Triplet &T1,Trplet &T2,Triplet &T3)
操作结果：将T1，T2相除，结果存入T3
} ADT Rational-Num

2.数据结构，函数说明

3.代码实现说明

相加

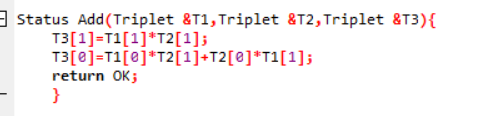
相减

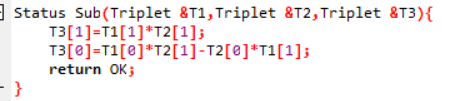
相乘

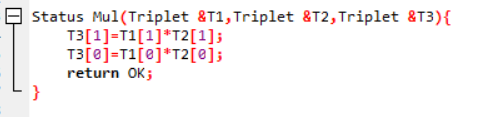
相除

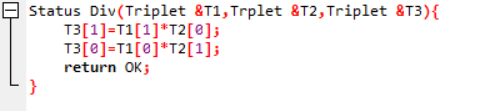
计算公约数方法：辗转相除法

运行结果

总结：学会了数据结构的运用，辗转相除法的运用