Project Euler 108：Diophantine reciprocals I 丢番图倒数I

Diophantine reciprocals I

In the following equation x, y, and n are positive integers.

For n = 4 there are exactly three distinct solutions:

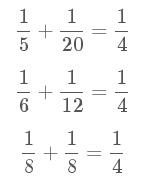
What is the least value of n for which the number of distinct solutions exceeds one-thousand?

NOTE: This problem is an easier version of Problem 110; it is strongly advised that you solve this one first.

---

丢番图倒数I

在如下方程中，x、y、n均为正整数。

对于n = 4，上述方程恰好有3个不同的解：

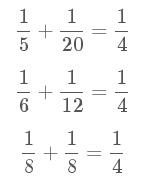
使得不同的解的数目超过1000的最小n值是多少？

注意：这个问题是第110题的简单版本；强烈推荐先解决这一题。

解题

这是一道很难的题目

先说暴力解法，普通暴力不行

1/x + 1/y = 1/n -> y = (n*x)/(x -n) 可以发现 只要 n*x能够整除（x-n）就是一个解了

能够找出x的范围就可以暴力解决

y = (n*x)/(x -n)  可以发现 x一定大于n，由于x y一定要是正数。

x=y=2n的时候上面等式也成了

假设x<=y 则y/x>=1  n/(x-n)>=1

2n>=x

x的取值范围就是n 到 2n

用javalong出现溢出的情况，Python好像时间很长，我用180180验证能够出来的

# coding=gbk

def run():
    for n in range(10,180181):
        count = 0
        for x in range(n+1,2*n+1):
            if (n*x)%(x-n)==0:
                count+=1
        if count>1000:
                    print n 

if __name__ == '__main__':
    run()
    

技巧性解题

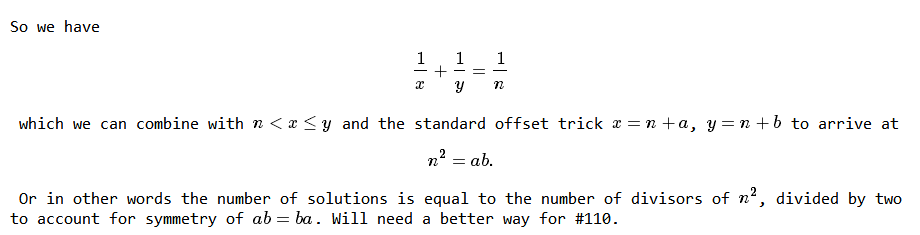
截图于mathblog

问题就转化为求d(N)  下面就很简单了

1，如何求许多素数，筛选法求素数

2，其他根据上面的就可以直接求解了

学会分析问题很重要，根据已学到的知识，解决没有见过的问题

package Level4;

import java.util.ArrayList;
import java.util.Collection;
import java.util.HashMap;
import java.util.Set;

public class PE0108{
    public static void run(){
        ArrayList<Integer> prime = getPrime(20);

        int n=2;
        while(true){

            int count = getDiophantine(n,prime);
            count = (count+1)/2;

            if(count> 500){
                System.out.println(n+"\t"+count);
                if(count>1000)
                break;
            }
            n++;
        }
    }
//    174720    608
//    175560    851
//    176400    563
//    177840    608
//    179520    527
//    180180    1013
    public static int getDiophantine(int n,ArrayList<Integer> prime){

        int count = 1;
        int i=0;
        for(i=0;i<prime.size();i++){
            int p = prime.get(i);

            int exp = 1;
            while(n %p ==0){
                exp+=2;
                n=n/p;
            }
            count *=exp;
            if(n==1)
                return count;
        }
        return count;
    }

    // 求 前num个素数
    public static ArrayList<Integer> getPrime(int num){
        ArrayList<Integer> prime=new ArrayList<Integer>();
        prime.add(2);
        // 除以已经判断是素数的数
        boolean isPrime = true;
        for(int i=3;prime.size()<num;i++){
            isPrime = true;
            for(int j=0;j<prime.size();j++){
                if(i%prime.get(j) ==0){
                    isPrime = false;
                    break;
                }
            }
            if(isPrime == true){
                prime.add(i);
            }
        }
        return prime;
    }
    public static void run1(){
        int MAX = 1000;
        int n=4;
        // 内存溢出使得程序运行错误
        System.out.println(getCount(180180));
        while(true){
            int count =getCount(n);

            if(count >=600){
                System.out.println(n+"\t"+count);
                if(count>MAX)
                break;
            }
            n++;
        }
    }
    public static int getCount(int n){
        int count =0;

        for(int x=n+1;x<=2*n;x++){
            long nx = n*x;
            System.out.println(nx);
            if( nx%(x-n)==0){
                count++;
            }
        }
        return count;
    }

    public static void main(String[] args){
        long t0 = System.currentTimeMillis();
        run1();
        long t1 = System.currentTimeMillis();
        long t = t1 - t0;
        System.out.println("running time="+t/1000+"s"+t%1000+"ms");
    }
}

Java Code