Poj2420 A Star not a Tree? 模拟退火算法

题目链接：http://poj.org/problem?id=2420

题目大意：每组数据中给n个点(n<=100)，求平面中一个点使得这个点到n个点的距离之和最小。

分析：一开始看到这个题想必是不好做的...因为平面太大了，不能使用枚举的方法，于是想到随机点出来比较。可是总不能无限的枚举，而且随机点出的答案需要是最优值还是一个玄学问题。所以想到了模拟退火的方法。

具体操作：首先随意找一个点作为出发点，然后设置一个初始温度，使得这个点可以在这个温度下乱跑[但是只让它往上下左右跑]温度越高，这个点就越活跃，在所找到的区域中选一个到其他点距离和最小的点，然后跳过去。完成这一步后，温度降低，再在新的点附近搜。联想到刚开始学模拟退火时看到的一张图：

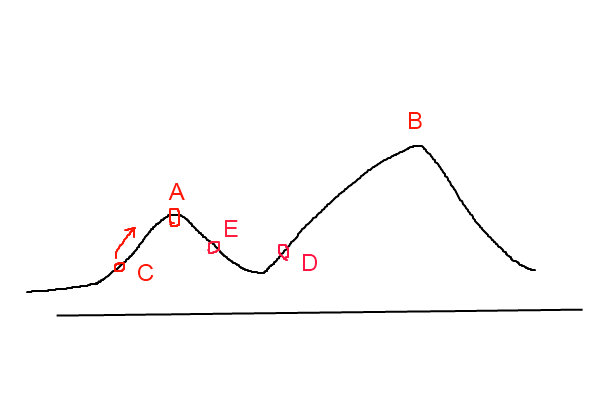
再配上一句经典的话：

爬山算法：兔子朝着比现在高的地方跳去。它找到了不远处的最高山峰。但是这座山不一定是珠穆朗玛峰。这就是爬山算法，它不能保证局部最优值就是全局最优值。

模拟退火：兔子喝醉了。它随机地跳了很长时间。这期间，它可能走向高处，也可能踏入平地。但是，它渐渐清醒了并朝最高方向跳去。这就是模拟退火。

可以把我们的题目想像到这个图中去：

　　山峰类似距离和的函数，求最小值相当于找最高峰，一开始允许随便找，就可以跨过第一座看上去是最高的峰顶而去往其他的位置。当时当温度降下来[或是酒慢慢醒了]就只能在比较近的位置找了，直到某个位置跳上了最高峰，得到最后的答案。

但是毕竟这个起始温度和降低温度的速度还是有些玄学的。所以不妨开得大一点保险好了...

AC代码

 #include<cstdio>
 #include<cmath>

 using namespace std;

 const int maxn=;
 const int T=;
 const int INF=0x7fffffff;
 const double eps=1e-;
 const double delta=0.98;

 struct Node{double x,y;}node[maxn];

 int n;
 int dx[]={,,,-};
 int dy[]={,-,,};

 inline double dis(Node A,Node B){
     return sqrt((A.x-B.x)*(A.x-B.x)+(A.y-B.y)*(A.y-B.y));
 }

 double sum_dis(Node A){
     double sum=;
     for(int i=;i<=n;i++)
         sum+=dis(A,node[i]);
     return sum;
 }

 void search(){
     Node Ans=node[],Now;
     double t=T,res=INF;
     bool find;
     while(t>eps){
         find=true;
         while(find){
             find=false;
             for(int j=;j<;j++){
                 Now.x=Ans.x+dx[j]*t;
                 Now.y=Ans.y+dy[j]*t;
                 double Dis=sum_dis(Now);
                 if(Dis<res)
                     res=Dis,Ans=Now,find=true;
             }
         }
         t=t*delta;
     }
     if(res-(int)(res)>0.5)
         printf("%d\n", (int)(res+));
     else
         printf("%d\n", (int)(res));
 }

 int main(){
 #ifndef ONLINE_JUDGE
     freopen("Poj2420.in","r",stdin);
     freopen("Poj2420.out","w",stdout);
 #endif

     while(~scanf("%d",&n)){
         for(int i=;i<=n;i++)
             scanf("%lf%lf",&node[i].x,&node[i].y);
         search();
     }

     return ;
 }