javascript实现数据结构与算法系列：栈 -- 顺序存储表示和链式表示及示例

栈（Stack）是限定仅在表尾进行插入或删除操作的线性表。表尾为栈顶（top），表头为栈底（bottom），不含元素的空表为空栈。

栈又称为后进先出（last in first out）的线性表。

堆栈可以用链表和数组两种方式实现，一般为一个堆栈预先分配一个大小固定且较合适的空间并非难事，所以较流行的做法是 Stack 结构下含一个数组。如果空间实在紧张，也可用链表实现，且去掉表头。

栈的链式表示结构图：

用js数组可以非常简单地实现栈的顺序表示，故这里不赘述。这里主要讲解一下栈的链式表示。

 // 找的链式表示
 function Stack() {
   this.top = null;
   this.size = 0;
 }
 module.exports = Stack;
 Stack.prototype = {
   constructor: Stack,
   push: function (data) {
     var node = {
       data: data,
       next: null
     };

     node.next = this.top;
     this.top = node;
     this.size++;
   },
   peek: function () {
     return this.top === null ?
       null :
       this.top.data;
   },
   pop: function () {
     if (this.top === null) return null;

     var out = this.top;
     this.top = this.top.next;

     if (this.size > 0) this.size--;

     return out.data;
   },
   clear: function () {
     this.top = null;
     this.size = 0;
   },
   displayAll: function () {
     if (this.top === null) return null;

     var arr = [];
     var current = this.top;

     for (var i = 0, len = this.size; i < len; i++) {
       arr[i] = current.data;
       current = current.next;
     }

     return arr;
   }
 };

 var stack = new Stack();

 stack.push(1);
 stack.push('asd');

 stack.pop();
 stack.push({a: 1});
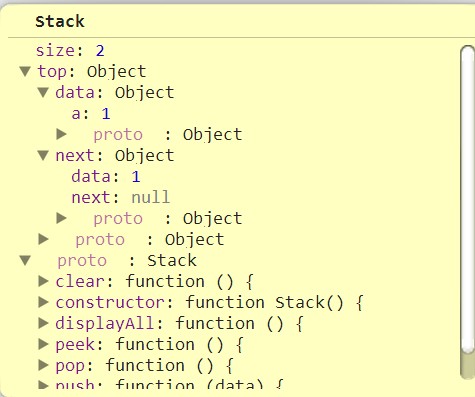
 console.log(stack);

相关单元测试：

 describe('stack tests', function(){
   var stack = new Stack();

   it('should push into stack', function(){
     stack.push(1);
     expect(stack.peek()).toBe(1);
     stack.push('asd');
     expect(stack.peek()).toBe('asd');
     expect(stack.size).toBe(2);
   });

   it('should pop from stack', function(){
     stack.pop();
     expect(stack.peek()).toBe(1);
     expect(stack.size).toBe(1);
     stack.push({a: 1});
     expect(stack.peek()).toEqual({a: 1});
     expect(stack.size).toBe(2);
   });

   it('should be an empty stack', function(){
     stack.pop();
     expect(stack.peek()).toBe(1);
     stack.pop();
     expect(stack.peek()).toBe(null);
     expect(stack.size).toBe(0);
   });
 });

堆栈的应用

• 回溯
• 递回
• 深度优先搜寻

示例1：数值进制转换

公式： N = (N / d) * d + N % d
N：十进制数值， d：需要转换的进制数

 function numTransform(number, rad) {
   var s = new Stack();

   while (number) {
     s.push(number % rad);
     number = parseInt(number / 8, 10);
   }

   var arr = [];
   while (s.top) {
     arr.push(s.pop());
   }
   console.log(arr.join(''));
 }

 numTransform(1348, 8);
 numTransform(1348, 2);

示例2：括号匹配检查

在算法中设置一个栈，每读入一个括号，若是右括号，则或者使置于栈顶的最急迫的期待得以消解，或者是不合法的情况；若是左括号，则作为一个新的更急迫的期待压入栈中，自然使得原有的在栈中的所有未消解的期待的急迫性都降一级。另外，在算法开始和结束时，栈都应该是空的。

 function bracketsMatch(str) {
   var stack = new Stack();
   var text = '';

   for (var i = 0, len = str.length; i < len; i++) {
     var c = str[i];
     if (c === '[') {
       stack.push(c);
     } else if (c === ']') {
       if (!stack.top || stack.pop() !== '[') throw new Error('unexpected brackets:' + c);
     } else {
       text += c;
     }
   }
   console.log(text);
 }

 console.log(bracketsMatch('[asd]'));

 function Matcher(left, right) {
   this.left = left;
   this.right = right;
   this.stack = new Stack();
 }
 Matcher.prototype = {
   match: function (str) {
     var text = '';

     for (var i = 0, len = str.length; i < len; i++) {
       var c = str[i];
       if (c === this.left) {
         this.stack.push(c);
       } else if (c === this.right) {
         if (!this.stack.top || this.stack.pop() !== this.left) {
           throw new Error('unexpected brackets:' + c);
         } else {
           text += ',';
         }
       } else {
         text += c;
       }
     }
     console.log(text);
     return text;
   }
 };
 var m = new Matcher('{', '}');
 m.match('[{123}123');

示例3：行编辑

当用户发现刚刚键入的一个字符是错的时，可补进一个退格符“#”,以表示前一个字符无效；如果发现当前键入的行内差错较多或难以补进，则可以键入一个退行符“@”

，以表示当前行中的字符均无效。

为此，可设这个输入缓冲区为一个栈结构，每当从终端接收了一个字符之后先做如下判断：

如果它既不是"#"也不是"@"，则将字符压入栈；

如果是"#"，则从栈顶删去一个字符；

如果是"@"，则清空栈。

 function LineEditor(str) {
   this.stack = new Stack();
   this.str = str || ''
 }
 LineEditor.prototype = {
   getResult: function () {
     var stack = this.stack;
     var str = this.str;
     for (var i = 0, len = str.length; i < len; i++) {
       var c = str[i];
       switch (c) {
         case '#':
           stack.pop();
           break;
         case '@':
           stack.clear();
           break;
         default:
           stack.push(c);
           break;
       }
     }

     var result = '';
     var current = stack.top;
     while (current) {
       result = current.data + result;
       current = current.next;
     }

     return result;
   }
 };

 var le = new LineEditor('whli##ilr#e(s#*s)\
     \noutcha@putchar(*s=#++)');
 console.log(le.getResult());

示例4：表达式求值

表达式求值是程序设计语言编译中的一个最基本问题、它的实现是栈应用的又一个典型例子。这里介绍一种简单直观，广为使用的算法，通常称为“运算符优先法”。

 // from： http://wuzhiwei.net/ds_app_stack/

 var prioty = {
   "+": 1,
   "-": 1,
   "%": 2,
   "*": 2,
   "/": 2,
   "^": 3,
   "(": 0,
   ")": 0,
   "`": -1
 };

 function doop(op, opn1, opn2) {
   switch (op) {
     case "+":
       return opn1 + opn2;
     case "-":
       return opn1 - opn2;
     case "*":
       return opn1 * opn2;
     case "/":
       return opn1 / opn2;
     case "%":
       return opn1 % opn2;
     case "^":
       return Math.pow(opn1, opn2);
     default:
       return 0;
   }
 }

 function opcomp(a, b) {
   return prioty[a] - prioty[b];
 }

 function calInfixExpression(exp) {
   var cs = [];
   var ns = [];
   exp = exp.replace(/\s/g, "");
   exp += '`';
   if (exp[0] === '-') {
     exp = "0" + exp;
   }
   var c;
   var op;
   var opn1;
   var opn2;
   for (var i = 0; i < exp.length; ++i) {
     c = exp[i];
     // 如果是操作符
     if (c in prioty) {
       // 如果右边不是左括号且操作符栈的栈顶元素优先权比右边大
       // 循环遍历进行连续运算
       while (c != '(' && cs.length && opcomp(cs[cs.length - 1], c) >= 0) {
         // 出栈的操作符
         op = cs.pop();
         // 如果不是左括号或者右括号，说明是运算符
         if (op != '(' && op != ')') {
           // 出栈保存数字的栈的两个元素
           opn2 = ns.pop();
           opn1 = ns.pop();
           // 将与操作符运算后的结果保存到栈顶
           ns.push(doop(op, opn1, opn2));
         }
       }
       // 如果右边不是右括号，保存到操作符栈中
       if (c != ')') cs.push(c);
     } else {
       // 多位数的数字的情况
       while (!(exp[i] in prioty)) {
         i++;
         c += exp[i];
       }
       ns.push(parseFloat(c));
       i--;
     }
   }
   return ns.length ? ns[0] : NaN;
 }

 var exp1 = calInfixExpression('5+3*4/2-2^3+5%2');
 console.log(exp1);

栈与递归调用的实现：

栈的另一个重要应用是在程序设计语言中实现递归调用。

递归调用：一个函数(或过程)直接或间接地调用自己本身，简称递归(Recursive)。

递归是程序设计中的一个强有力的工具。因为递归函数结构清晰，程序易读，正确性很容易得到证明。

为了使递归调用不至于无终止地进行下去，实际上有效的递归调用函数(或过程)应包括两部分：递推规则(方法)，终止条件。

为保证递归调用正确执行，系统设立一个“递归工作栈”，作为整个递归调用过程期间使用的数据存储区。

每一层递归包含的信息如：参数、局部变量、上一层的返回地址构成一个“工作记录” 。每进入一层递归，就产生一个新的工作记录压入栈顶；每退出一层递归，就从栈顶弹出一个工作记录。

从被调函数返回调用函数的一般步骤：

(1) 若栈为空，则执行正常返回。

⑵ 从栈顶弹出一个工作记录。

⑶ 将“工作记录”中的参数值、局部变量值赋给相应的变量；读取返回地址。

⑷ 将函数值赋给相应的变量。

(5) 转移到返回地址。

相关：

javascript实现数据结构与算法系列