机器人学 —— 机器人视觉（Bundle Adjustment）
今天完成了机器人视觉的所有课程以及作业，确实是受益匪浅啊！
最后一个话题是Bundle Adjustment. 机器人视觉学中，最顶尖的方法。
1、基于非线性优化的相机位姿估计
之前已经在拟合一篇中，已经补完了非线性最小二乘拟合问题。Bundle Adjustment，中文是光束平差法，就是利用非线性最小二乘法来求取相机位姿，三维点坐标。在仅给定相机内部矩阵的条件下，对四周物体进行高精度重建。Bundle Adjustment的优化目标依旧是最小重复投影误差。
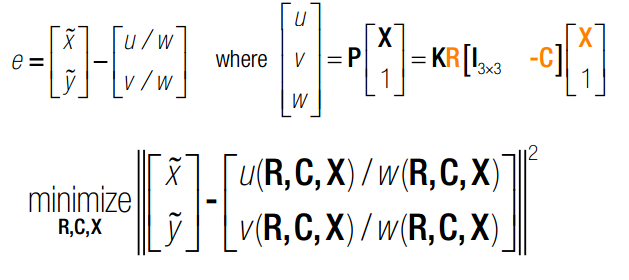
与利用non-linear mean square 解三角同，bundle adjustment 中所有的参数，RCX均为变量。N幅图则有N个位姿，X个点，我们会得到非常大的jacobbian Matrix.本质上，需要使用雅克比矩阵进行梯度下降搜索。详细见博客——拟合
2、雅克比矩阵
雅克比矩阵的行代表信息，列代表约束
每一行是一个点在该位姿下的误差，每一列代表f对x分量的偏导数。
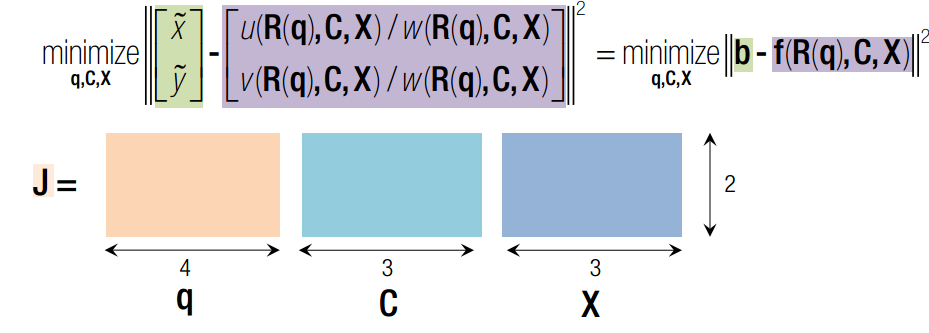
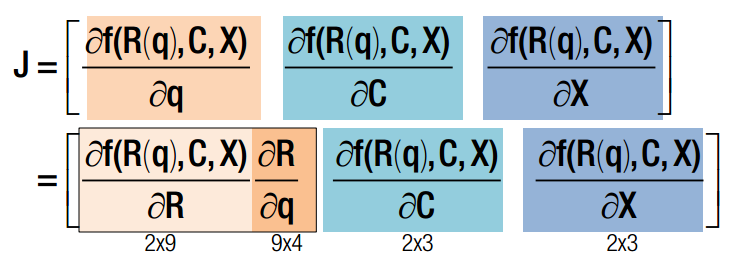
q x c 均为变量，q是旋转四元素，x 是三维点空间坐标，c 是相机光心在世界坐标系下的坐标。J 可以分为三部分，前4列代表对旋转求导，中间三列代表对c求导，最后三列代表对x求导。其中，对旋转求导又可以分解为对旋转矩阵求导X旋转矩阵对四元素q求导。一旦获得J的表达式，我们就可以使用Newton-Gaussian 迭代对x寻优了。求导后的数学表达式如下：
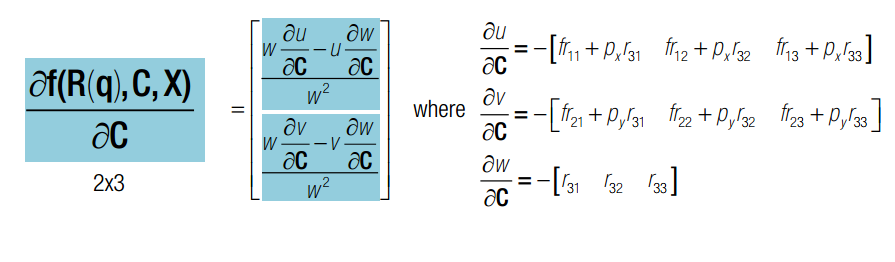
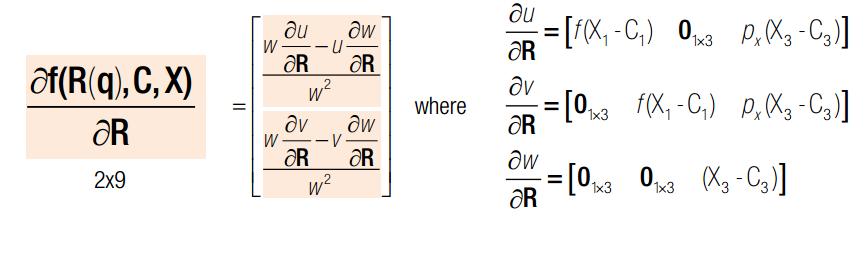
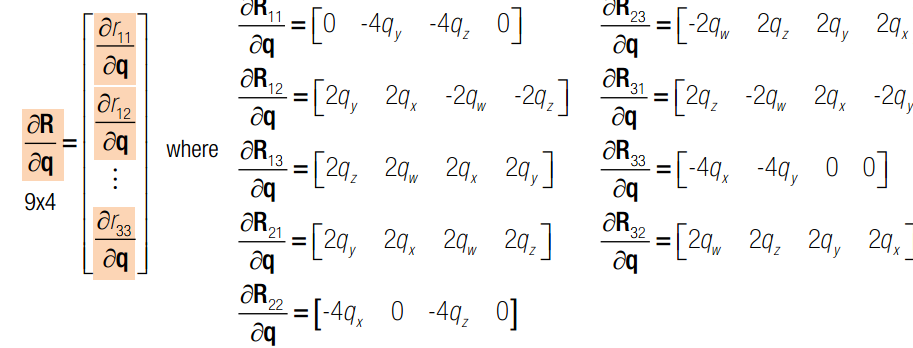
如果有两个相机，则总的雅克比矩阵如下：
通过同时迭代所有的q C X ，最终可以同时得到世界点坐标，相机位姿 == SLAM!!!
机器人学 —— 机器人视觉（Bundle Adjustment）的更多相关文章
- Bundle Adjustment光束平差法概述
http://blog.csdn.net/abcjennifer/article/details/7588865 http://blog.csdn.net/ximenchuixuezijin/arti ...
- 机器人学 —— 机器人感知（Gaussian Model）
机器人感知是UPNN机器人专项中的最后一门课程,其利用视觉方法来对环境进行感知.与之前提到的机器人视觉不同,机器人感知更侧重于对环境物体的识别与检测.与计算机视觉不同,机器人视觉所识别的物体往往不需要 ...
- bundle adjustment 玩具程序
结合 bundle adjustment原理(1) 和 Levenberg-Marquardt 的 MATLAB 代码 两篇博客的成果,调用MATLAB R2016a中 bundleAdjustmen ...
- bundle adjustment原理(1)
那些光束平差的工具,比如SBA.SSBA之类的虽然好,然而例子和教程都不够多且不够详细,让初学者难以上手. 要传入的参数虽然有解释,然而却也不是十分清楚其含义,具体要怎么生成,生成为什么形式. 我在折 ...
- bundle adjustment原理(1)转载
转自菠菜僵尸 http://www.cnblogs.com/shepherd2015/p/5848430.html bundle adjustment原理(1) 那些光束平差的工具,比如SBA.SSB ...
- 机器人学 —— 机器人感知（Kalman Filter）
对于机器人感知任务而言,经常需要预判物体的运动,保证机器人在物体与自身接触之前进行规避.比如无人机与障碍物的碰撞,足球机器人判断足球的位置.预判的前提是对当前状态进行准确的估计,比如足球的速度,障碍物 ...
- 机器人学 —— 机器人感知（Location）
终于完成了Robotic SLAM 所有的内容了.说实话,课程的内容比较一般,但是作业还是挺有挑战性的.最后一章的内容是 Location. Location 是 Mapping 的逆过程.在给定ma ...
- 机器人学 —— 机器人感知（Mapping）
对于移动机器人来说,最吸引人的莫过于SLAM,堪称Moving Robot 皇冠上的明珠.Perception 服务于 SLAM,Motion Plan基于SLAM.SLAM在移动机器人整个问题框架中 ...
- VIO的Bundle Adjustment推导
IMU模型和运动积分 $R_{\tiny{WB}} \left( t +\Delta{t} \right) = R_{\tiny{WB}} \left( t \right) Exp\left( \in ...
随机推荐
- Ext中如何校验TextField的字段被修改了？
场景描述: 在form表单中有个sfzhm的字段,需要去后台进行sfzhm是否重复的校验,一开始使用了blur的event来去后台进行校验,后来发现在焦点离开时,及时数据没有发生变化,也会造 ...
- 装载：对CSS中的Position、Float属性的一些深入探讨
对CSS中的Position.Float属性的一些深入探讨 对CSS中的Position.Float属性的一些深入探讨 对于Position.Float我们在平时使用上可以说是使用频率非常高的两个 ...
- JS--中的 Cookie 与存储
Cookie 主要是在客户端进行一些简单的数据存储等,使用来提供本地化存储的脚本功能.Cookie 的处理环境本身是需要在服务器下进行的,但是现在的大部分浏览器都已经支持Cookie本地化的存储于处理 ...
- Application, JDBC, 数据库连接池, Session, 数据库的关系
RT,这几个东东已经困扰我很长一段时间了... 这次争取把她们理清楚了! 参考资料: 1. 数据库连接池:http://www.cnblogs.com/shipengzhi/archive/2011/ ...
- opencv中的Bayes分类器应用实例
转载:http://blog.csdn.net/yang_xian521/article/details/6967515 PS:很多时候,我们并不需要特别精通某个理论,而且有的时候即便你非常精通,但是 ...
- Leetcode#148 Sort List
原题地址 链表归并排序 真是恶心的一道题啊,哇了好多次才过. 代码: void mergeList(ListNode *a, ListNode *b, ListNode *&h, ListNo ...
- Leetcode#49 Anagrams
原题地址 Anagram:变位词.两个单词是变位词关系的条件是:组成单词的字符相同,只是顺序不同 第一次看这道题看了半天没明白要干嘛,丫就不能给个样例输入输出么..后来还是看网上其他人的总结知道是怎么 ...
- PHP 扩展库
表 6.1. PHP 扩展库 扩展库 说明 注解 php_bz2.dll bzip2 压缩函数库 无 php_calendar.dll 历法转换函数库 自 PHP 4.0.3 起内置 php_cpdf ...
- Spring.net Could not load type from string value
最近有点懒了啊,都没有按时上来博客园更新下,个人觉得遇到难题的时候在这里留下脚印也亦造福他人,进来 晓镜水月 被项目围的团团转,asp.net MVC项目来的,但是我还是不务正业啊,在弄网络爬虫,这个 ...
- c# 与flash通信简介
许久不曾写随笔,即使许久的怠惰,是该抬抬头,看看天了. 公司项目,项目要求是在winForm端先获取下位机的肌电信号采集数据,然后根据这些数据的变化来控制flash游戏,这样一些患者在flash游戏中 ...