【思维题 集合hash 树上差分】11.5撸树

要注重问题的转化和一些结论的推断

题目描述

要致富，先撸树。

一棵树的形状可以简化为一张 $N$ 个点 $M$ 条边的图，由于装备条件限制，你只有撸两次，也就是删去两条边，当这张图不联通时，就意味着树倒了。

现在你想知道有多少种方案能撸倒这棵树。

输入格式

第一行两个正整数 $n,m$

接下来 $m$ 行，每行两个正整数，表示一条边。

输出格式

输出一个数，表示方案数。

数据规模与约定

对于 $30\%$ 的数据，$1\le N\le 20，1\le M\le40$

对于$50\%$的数据，$1\le N\le500，1\le M\le1000$

对于$100\%$的数据，$1\le N\le50000，1\le M\le100000$

保证刚开始图是联通的。

时间限制:1s

空间限制:512M

---

题目分析

题外话

有重边

好好分析一下

图的问题先转化为树，于是先预处理出树边与非树边，再来考虑非树边对于树的影响。

首先是一些定义：对每一条边，如果是树边就使用哈希记录下经过它的非树边，并将这个哈希值称作“经过哈希值”、边的数量称作“经过数”；如果是非树边，“经过哈希值”就是它的哈希值本身、“经过数”不计。

然后是结论：若一条边（树边）的经过数为0（也就意味着它是一条割边），说明选了它再任选一条边都可行；若两条边的经过哈希值相同，意味着必须同时取两条这种边才能将图分为两半。

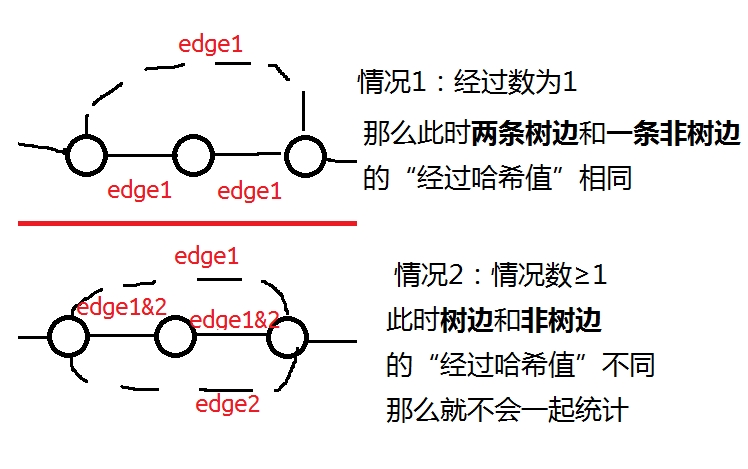
接下去考虑算法实现。

注意到这里哈希是集合哈希，那么一种经典方法就是rand一个大数（long long），再异或起来。对于一条非树边$(u,v)$，我们需要把树上路径$u->v$这一段都加上标记，因此考虑树上差分。这里有一个小技巧，因为此处操作是异或，而两端点同时异或一个相同的数，那么就不用像常规那样求出lca并除去贡献，只需要在打完标记之后再从上至下dfs一遍记录每一条边的哈希值。

还有一个处理的技巧：将哈希开成unsigned long long；双哈希开std::pair。如此一来排序时候就自然而然将经过数为0的边排在前面，天然保证了答案的顺序。

 #include<bits/stdc++.h>
 typedef unsigned long long ll;
 typedef std::pair<ll, ll> pr;
 const int maxn = ;
 const int maxm = ;

 struct Edge
 {
     int v,id;
     Edge(int a=, int b=):v(a),id(b) {}
 }edges[maxm];
 int n,m,u[maxm],v[maxm],fa[maxn];
 int edgeTot,head[maxn],nxt[maxm];
 pr eval[maxm],ev[maxn];
 ll ans;

 int read()
 {
     char ch = getchar();
     int num = ;
     bool fl = ;
     for (; !isdigit(ch); ch=getchar())
         if (ch=='-') fl = ;
     for (; isdigit(ch); ch=getchar())
         num = (num<<)+(num<<)+ch-;
     if (fl) num = -num;
     return num;
 }
 pr operator ^(pr a, pr b){return pr(a.first^b.first, a.second^b.second);}
 int get(int x){return x==fa[x]?x:fa[x]=get(fa[x]);}
 void addedge(int u, int v, int id)
 {
     edges[++edgeTot] = Edge(v, id), nxt[edgeTot] = head[u], head[u] = edgeTot;
     edges[++edgeTot] = Edge(u, id), nxt[edgeTot] = head[v], head[v] = edgeTot;
 }
 void count(int x, int fa)
 {
     for (int i=head[x]; i!=-; i=nxt[i])
     {
         int v = edges[i].v, id = edges[i].id;
         if (v!=fa)
             count(v, x), ev[x] = ev[x]^ev[v], eval[id] = ev[v];
     }
 }
 int main()
 {
     freopen("lutree.in","r",stdin);
     freopen("lutree.out","w",stdout);
     memset(head, -, sizeof head);
     srand(), n = read(), m = read();
     for (int i=; i<=n; i++) fa[i] = i;
     for (int i=,uf,vf; i<=m; i++)
     {
         uf = get(u[i] = read()), vf = get(v[i] = read());
         if (uf^vf){
             addedge(u[i], v[i], i), fa[uf] = vf;
         }else{
             eval[i] = pr(1ll*rand()*rand()*rand()*rand()*rand(), 1ll*rand()*rand()*rand()*rand()*rand());
         }
     }
     for (int i=; i<=m; i++)
         if (eval[i].first||eval[i].second){
             ev[u[i]] = ev[u[i]]^eval[i], ev[v[i]] = ev[v[i]]^eval[i];
         }
     count(, );
     std::sort(eval+, eval+m+);
     for (int i=, j=; i<=m; i=j)
     {
         if ((eval[i].first==)&&(eval[i].second==))
             ans += m-i, j = i+;
         else{
             for (j=i; j<=m&&eval[i]==eval[j]; j++);
             ans += 1ll*(j-i-)*(j-i)/2ll;
         }
     }
     printf("%lld\n",ans);
     return ;
 }

END