再回首数据结构—AVL树（二）

前面主要介绍了AVL的基本概念与结构，下面开始详细介绍AVL的实现细节；

AVL树实现的关键点

　　AVL树与二叉搜索树结构类似，但又有些细微的区别，从上面AVL树的介绍我们知道它需要维护其左右节点平衡，实现AVL树关键在于标注节点高度、计算平衡因子、维护左右子树平衡这三点，下面分别介绍；

标注节点高度

　　从上面AVL树的定义中我们知道AVL树其左右节点高度差不能超过一，所以我们需要标注出每个节点高度；

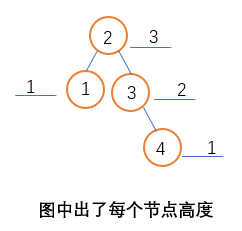
　　1、节点高度为最大的子节点高度加1，其中叶子节点高度为1；

　　2、1与4叶子节点高度为1，节点3高度为节点4的高度加1，节点2高度为1与3节点中最大的高度加1；

　　3、节点初始化时高度为1，当在AVL中添加与删除节点时需要维护其节点高度，在AVL添加节点后需要重新计算当前添加节点的高度；

计算平衡因子

　　标注了每个节点高度后此时可以轻松算出每个节点的平衡因子，只需其节点左子树与右子树的高度差的绝对值即可；

　　1、1、4叶子节：平衡因子为0

　　2、节点3：右子树高度为1，左子树其高度为0，0-1绝对值为1，此节点平衡因子为1

　　3、节点2：左子树高度为1，右子树高度为2，1-2绝对值为1，此节点平衡因子为1

维护左右子树平衡

　　当在AVL中添加与删除节点时都可能造成AVL变成失去平衡状态使之退化为二叉搜索树，AVL中主要在添加节点与删除节点时需要维护其左右子树的平衡因子；

添加节点

　　添加节点最终都是添加到叶子节点上，节点添加后其先祖节点可能出现了失去平衡的情况，需要从添加的节点开始向上维护平衡性，向上查找不平衡节点；

右旋转

　　新增节点在不平衡节点左侧的左侧，同时不平衡节点左子树高度大于等于右子树高度（左子树平衡因子大于等于右子树平衡因子）；

　　添加节点1后第一个不平衡节点为节点3，同时节点3左子树高度大于右子树高度，此时需要不平衡节点向右旋转；

通过如下操作完成节点右旋转；

 T = 2.right

 2.right = 3

 3.left = T

左旋转

　　新增节点在不平衡节点右侧的右侧，同时不平衡节点右子树高度大于等于左子树高度（右子树平衡因子大于等于左子树平衡因子）；

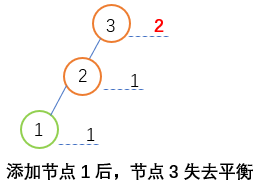
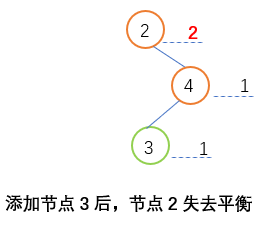
添加节点3后，节点1失去平衡添加节点3后第一个不平衡节点为节点1，同时节点1右子树高度大于左子树高度，此时需要不平衡节点向左旋转；

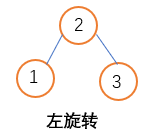
通过如下操作完成节点左旋转；

 T = 2.left

 2.left = 1

 1.right = T

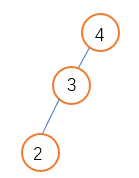
先左旋转后右旋转

新增节点在不平衡节点左侧的右侧

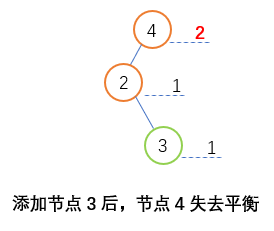
先左旋转，变成了右旋转问题，重复上面说所的右旋转；

 T = 4.left

 Y = T.right

 Z = Y.left

 Y.left = T

 T.right = Z

 4.left = Y

先右旋转后左旋转

新增节点在不平衡节点右侧的左侧

先右旋转，变成了左旋转问题，重复上面说所的左旋转；

 T = 2.right

 Y = T.left

 Z = Y.right

 Y.right = T

 T.left = Z

 2.right = Y

删除节点

　　删除节点是AVL树也可能会失去平衡，因此也需要维护AVL的平衡性；

节点的删除右这么几个步骤：

1、要删除的节点比当前节点小时在左子树查找

2、要删除的节点比当前节点大时在右子树查找

3、要删除节点为当前节点且左子树为空时右子树顶上

4、要删除节点为当前节点且右子树为空时左子树顶上

5、要删除节点左右子树均存在时，大于当前节点的最小节点顶上

6、更新节点高度值

7、计算节点平衡因子

8、进行与添加节点时一样的平衡因子维护操作

文章首发地址：Solinx

http://www.solinx.co/archives/1330