【Sprint3冲刺之前】项目可行性研究报告

TD校园手机助手软件可行性研究报告

1.引言

在信息化时代高速发展的今天，手机成了每个人的必备物品之一。随着科技的迅猛发展，人们已经不仅仅满足于用手机发短信，打电话，因此，android手机应运而生，特别是近几年，其发展的速度更是惊人，它还提供了听歌、看视频、用蓝牙传输数据、玩游戏、上网等功能。我们的生活因此更加方便。为了更好地服务于铁大的学生，我们研究出一款校园手机助手的软件，方便同学们的生活。

1.1背景

1.1.1Android发展背景

Android是一套真正意义的开放性移动设备综合平台，它包括操作系统、中间件和一些关键的平台应用。Android的Java程序运行环境包含一组Java核心函数库及Dalvik虚拟机，他们有效地优化了Java程序的运行过程。Android系统平台基于优化了的Linux内核，它提供诸如内存管理、进程管理、设备驱动等服务，同时也是手机硬件的连接层。

Android最大的优点在于它是一个开放的体系结构，具有非常好的开发和调试环境，而且还制成各种可扩展的用户体验，Android里面有非常丰富的图形系统，对多媒体的支持功能和非常强大的浏览器。

Android平台的开放性特点既能促进技术的创新，又有助于降低开发成本，还可以使运营商能非常方便地地址特色化产品，因此，它具有很大的市场发展潜力。

1.1.2软件开发背景

本软件名称为TD校园手机助手，开发的初衷是在软件工程课上老师安排我们的作业，我们小组成员在老师的指点以及大家的商讨下，决定开发本软件。本软件是特别针对铁道大学内部学生所开发的软件，针对大家的衣食住行等方面的建议，并提供日程信息的增加、删除、修改等功能，方便同学管理自己的生活。同时，以3D效果的形式展现学校的美景美图，让大家足不出户了解和欣赏校园的美景。

2.可行性研究的前提

通过本软件，希望能够解决本校学生在生活中的衣食住行以及上自习和上课教室的问题和平时的日程管理的问题。

2.1软件功能及要求

2.1.1学生日程管理

（1）日程的增、删、改、查。添加事件包括：学生实验、练习、所做项目、会议情况；对于平时的生活进行规划和调整，合理地安排生活和学习。

（2）以时间表的形式，在日历里管理并显示日程的进展情况。按主题显示学生每学期任务的安排、计划、完成情况，方便用户获知信息；通过主界面用户可以知道自己的行程安排、每日安排以及实现跳转其他界面的功能；以日历界面的形式显示自己的行程安排，并可以及时进行日程的更改以及删除和添加，添加时可以使统一事件在不同时间同时添加，即可以进行批量处理，方便用户使用。

2.1.2TD美景美图

以3D效果的形式展示铁大校园美景，同时，加上同学们参加学校摄影大赛的作品进行展示。以3D模拟的形式展现出来，给人以视觉冲击，通过多组图片的展示，向大家展示出一个美丽的铁大校园。

2.1.3TD生活手册

对铁道大学周边的衣、食、住、行等方面向同学们进行推荐，方便同学们的出行。同时，对学校的一些组织做一些广告，方便学校同学更好地了解并参与学校的社团活动，给大学生一个锻炼自己的平台。

2.1.4GPS导航

本功能主要面向大一新生，新生可以通过本导航更快地了解学校的各方面情况，更好地适应和规划大学生活。通过地图的形式，显示用户所处位置，并通过查询所到目的地，显示路径和最短路径，节省用户时间和精力。

2.2目标

由于本软件是针对本校学生开发的，最终希望通过本软件，大家能够更好地安排自己的大学生活，解决生活中的不便。0

3.对现有系统的分析

3.1数据处理流程和数据流程

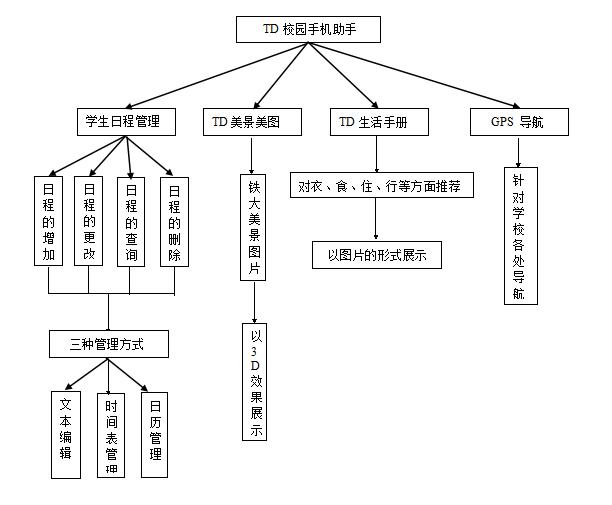
3.2局限性及改进方法

由于本软件还处于开发初期，时间的限制导致一些功能无法实现，在后续开发中我们会添加其他大学的课程等信息而不仅仅是局限在铁大一个校园里，方便同学查询和了解。