codeforces 569C C. Primes or Palindromes?(素数筛+dp)

题目链接：

C. Primes or Palindromes?

time limit per test

3 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Rikhail Mubinchik believes that the current definition of prime numbers is obsolete as they are too complex and unpredictable. A palindromic number is another matter. It is aesthetically pleasing, and it has a number of remarkable properties. Help Rikhail to convince the scientific community in this!

Let us remind you that a number is called prime if it is integer larger than one, and is not divisible by any positive integer other than itself and one.

Rikhail calls a number a palindromic if it is integer, positive, and its decimal representation without leading zeros is a palindrome, i.e. reads the same from left to right and right to left.

One problem with prime numbers is that there are too many of them. Let's introduce the following notation: π(n) — the number of primes no larger than n, rub(n) — the number of palindromic numbers no larger than n. Rikhail wants to prove that there are a lot more primes than palindromic ones.

He asked you to solve the following problem: for a given value of the coefficient A find the maximum n, such that π(n) ≤ A·rub(n).

Input

The input consists of two positive integers p, q, the numerator and denominator of the fraction that is the value of A (, ).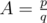

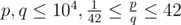Output

If such maximum number exists, then print it. Otherwise, print "Palindromic tree is better than splay tree" (without the quotes).

Examples

input

1 1

output

40

input

1 42

output

1

input

6 4

output

172

题意：

问满足pi[n]/rub[n]<=p/q的最大的n是多少;

思路：

pi[i]和rub[i]都随着i的增大而增大,且pi[i]/rub[i]的值也随着增大,(小于10的数特殊);p/q给有范围,可以算一下大约1200000时pi[i]/rub[i]已经大约42了;所以暴力找到那个最大的n;

AC代码：

/*2014300227    569C - 28    GNU C++11    Accepted    61 ms    14092 KB*/
#include <bits/stdc++.h>
using namespace std;
const int N=12e5+;
typedef long long ll;
const double PI=acos(-1.0);
int p,q,pi[N],vis[N],rub[N];
void get_pi()//素数筛+dp得到pi[i]
{
    memset(pi,,sizeof(pi));
    pi[]=;
    for(int i=;i<N;i++)
    {
        if(!pi[i])
        {
            for(int j=;j*i<N;j++)
            {
                pi[i*j]=;
            }
            pi[i]=pi[i-]+;
        }
        else pi[i]=pi[i-];
    }
}
int is_pal(int x)//判断一个数是不是回文数;
{
    int s=,y=x;
    while(y)
    {
        s*=;
        s+=y%;
        y/=;
    }
    if(s==x)return ;
    return ;
}
void get_rub()
{
    rub[]=;
    for(int i=;i<N;i++)
    {
        if(is_pal(i))rub[i]=rub[i-]+;
        else rub[i]=rub[i-];
    }
}
int check(int x)
{
    if(pi[x]*q<=p*rub[x])return ;
    return ;

}
int get_ans()
{
    int ans=;
    for(int i=;i<N;i++)
    {
        if(check(i))ans=i;
    }
    if(ans==)printf("Palindromic tree is better than splay tree\n");
    else printf("%d\n",ans);
}
int main()
{
    get_pi();
    get_rub();
    //cout<<pi[1200000]*1.0/(rub[1200000]*1.0);
    scanf("%d%d",&p,&q);
    get_ans();

    return ;
}