【HDU3802】【降幂大法+矩阵加速+特征方程】Ipad,IPhone

Problem Description

In ACM_DIY, there is one master called “Lost”. As we know he is a “-2Dai”, which means he has a lot of money.
  
Well, Lost use Ipad and IPhone to reward the ones who solve the following problem.
  
In this problem, we define F( n ) as :
  
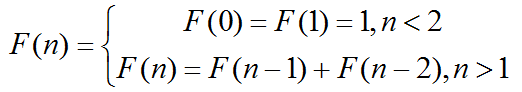
Then Lost denote a function G(a,b,n,p) as

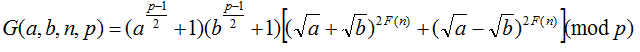
Here a, b, n, p are all positive integer!
If you could tell Lost the value of G(a,b,n,p) , then you will get one Ipad and one IPhone!

 

Input

The first line is one integer T indicates the number of the test cases. (T <= 100)
Then for every case, only one line containing 4 positive integers a, b, n and p.
(1 ≤a, b, n, p≤2*10⁹ , p is an odd prime number and a,b < p.)

 

Output

Output one line,the value of the G(a,b,n,p) .

 

Sample Input

4
2 3 1 10007
2 3 2 10007
2 3 3 10007
2 3 4 10007

 

Sample Output

40
392
3880
9941

 

Author

AekdyCoin

 

Source

ACM-DIY Group Contest 2011 Spring

 

Recommend

notonlysuccess   |   We have carefully selected several similar problems for you:  3805 3800 3801 3803 3804

【分析】

不知道怎么回事...跟网上的程序对拍了好像没错，怎么过不了...应该是有些比较坑的点....

不错的一道题目，前面的两项不说了，后面的那一项可以把二次方弄进去，然后变成一个用韦达定理做一个逆运算得到特征方程。

然后就有递推式了，然后就可以矩阵加速了。

然后因为幂实在是太大了，然后上降幂大法，然后没了。

其实还涉及到二次剩余的理论，如果前面没有那两个式子答案就错了....因为刚好是那两个式子，让不能用降幂大法的情况变成0...

 /*
 五代李煜
 《相见欢·林花谢了春红》
 林花谢了春红，太匆匆。无奈朝来寒雨晚来风。
 胭脂泪，相留醉，几时重。自是人生长恨水长东。
 */
 #include <iostream>
 #include <cstdio>
 #include <ctime>
 #include <cmath>
 #include <algorithm>
 #include <cstring>
 #include <string>
 #include <map>
 #include <set>
 #include <vector>
 #define LOCAL
 const int MAXN =  + ;
 const int INF = 0x7fffffff;
 using namespace std;
 typedef long long ll;
 ll mod;//代表取模的数字
 ll check, a, b, n, p;
 struct Matrix{
        ll num[][];
        //Matrix(){memset(num, 0, sizeof(num));}
 };
 //为了防止和第一种矩阵乘法搞混
 Matrix Mod(Matrix A, Matrix B, ll k){
      if (k == ){//代表两种不同的乘法
         Matrix c;
         memset(c.num, , sizeof (c.num));
         for (ll i = ; i <= ; i++)
         for (ll j = ; j <= ; j++)
         for (ll k = ; k <= ; k++){
             ll tmp = (A.num[i][k] * B.num[k][j]);
             if (check) tmp %= (p - );
             c.num[i][j] += tmp;
             if (check) c.num[i][j] %= (p - );
         }
         //一旦大于了p-1代表当前出现的斐波那契数列会大于phi(p)，可以使用降幂大法
         if ((c.num[][] + c.num[][]) > (p - )) check = ;
         return c;
      }else if (k == ){
            Matrix C;
            memset(C.num, , sizeof(C.num));
            for (ll i = ; i <= ; i++)
            for (ll j = ; j <= ; j++)
            for (ll k = ; k <= ; k++) {
                C.num[i][j] += (A.num[i][k] * B.num[k][j]) % p;
                C.num[i][j] = ((C.num[i][j] % p) + p) % p;
            }
            return C;
      }
 }
 //得到第x位的斐波那契数，也就是获得指数
 Matrix Matrix_pow(Matrix A, ll x, ll k){
        if (x == ) return A;
        Matrix tmp = Matrix_pow(A, x / , k);
        if (x %  == ) return Mod(tmp, tmp, k);
        else return Mod(Mod(tmp, tmp, k), A, k);
 }
 ll get(ll x){
      if (x == ) return ;
      else if (x == ) return ;
      Matrix A, B;
      A.num[][] = ; A.num[][] = ;
      A.num[][] = ; A.num[][] = ;
      x--;//为真实的需要乘的次数
      if (x == ) return ;
      B = Matrix_pow(A, x, );
      if (B.num[][] + B.num[][] > (p - )) check = ;
      if (check == ) return B.num[][] + B.num[][];
      else return (B.num[][] + B.num[][]) % (p - ) + p - ;
 }
 //有了a,b,pos就可进行矩阵加速了
 ll cal(ll a, ll b, ll pos){
     if (pos == ) return  % p;
     else if (pos == ) return  ( * (a + b)) % p;
     Matrix A;
     A.num[][] = ( * (a + b)) % p; A.num[][] = (((-(a - b) * (a - b)) % p) + p) % p;
     A.num[][] = ; A.num[][] = ;
     pos--;
     Matrix B;
     B = Matrix_pow(A, pos, );
     return (B.num[][] * A.num[][]) % p + (B.num[][] * ) % p;
 }
 ll pow(ll a, ll b){
     if (b == ) return  % p;
     if (b == ) return a % p;
     ll tmp = pow(a, b / );
     if (b %  == ) return (tmp * tmp) % p;
     else return (((tmp * tmp) % p) * a) % p;
 }

 int main(){
     int T;
     scanf("%d", &T);
     while (T--){
           //for (int i = 1; i ，=)
           scanf("%lld%lld%lld%lld", &a, &b, &n, &p);
           check = ;//判断f(n)是否大于p
           ll pos = get(n);
           ll Ans = cal(a, b, pos);
           ll f1, f2;
           f1 = (pow(a, (p - ) / ) + ) % p;
           f2 = (pow(b, (p - ) / ) + ) % p;
           Ans = (((f1 * f2) % p) * Ans) % p;
           printf("%lld\n", Ans);
     }
     //p = 0x7fffffff;
     //printf("%lld", get(5));
     //for (int i = 0; i <= 10; i++) printf("%lld\n", get(i));
     return ;
 }