BZOJ1001 BJOI2006 狼抓兔子

Description

---

现在小朋友们最喜欢的"喜羊羊与灰太狼",话说灰太狼抓羊不到，但抓兔子还是比较在行的，而且现在的兔子还比较笨，它们只有两个窝，现在你做为狼王，面对下面这样一个网格的地形：

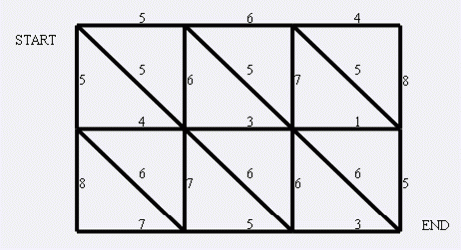
左上角点为(1,1),右下角点为(N,M)(上图中N=3,M=4).有以下三种类型的道路

1:(x,y)<==>(x+1,y)

2:(x,y)<==>(x,y+1)

3:(x,y)<==>(x+1,y+1)

道路上的权值表示这条路上最多能够通过的兔子数，道路是无向的. 左上角和右下角为兔子的两个窝，开始时所有的兔子都聚集在左上角(1,1)的窝里，现在它们要跑到右下角(N,M)的窝中去，狼王开始伏击这些兔子.当然为了保险起见，如果一条道路上最多通过的兔子数为K，狼王需要安排同样数量的K只狼，才能完全封锁这条道路，你需要帮助狼王安排一个伏击方案，使得在将兔子一网打尽的前提下，参与的狼的数量要最小。因为狼还要去找喜羊羊麻烦。

Input：

---

第一行为N,M.表示网格的大小，N,M均小于等于1000.

接下来分三部分

第一部分共N行，每行M-1个数，表示横向道路的权值.

第二部分共N-1行，每行M个数，表示纵向道路的权值.

第三部分共N-1行，每行M-1个数，表示斜向道路的权值.

Output：

---

输出一个整数，表示参与伏击的狼的最小数量.

Solution

---

转化为网络流，把每个有直接连边的点之间连一条权为X的边，然后跑一边最大流即可。

 //Writer : Hsz %WJMZBMR%tourist%hzwer
 #include<iostream>
 #include<cstring>
 #include<cstdio>
 #include<cmath>
 #include<queue>
 #include<map>
 #include<set>
 #include<stack>
 #include<vector>
 #include<cstdlib>
 #include<algorithm>
 #define LL long long
 using namespace std;
 const int S=,N=,M=,inf=0x3fffffff;
 int to[M],val[M],nxt[M],h[N],head[N],ecnt=,T;
 int n,m;
 void add(int bg,int ed,int v) {
     to[++ecnt]=ed;
     nxt[ecnt]=head[bg];
     val[ecnt]=v;
     head[bg]=ecnt;
 }
 void ins(int bg,int ed,int x) {
     add(bg,ed,x);
     add(ed,bg,x);
 }
 bool bfs() {
     memset(h,-,sizeof h);
     h[S]=;
     queue<int>q;
     q.push(S);
     while(!q.empty()) {
         int u=q.front();
         q.pop();
         for(int i=head[u]; i; i=nxt[i]) {
             if(val[i]&&h[to[i]]==-) {
                 h[to[i]]=h[u]+;
                 q.push(to[i]);
             }
         }
     }
     return h[T]!=-;
 }
 int dfs(int x,int f) {
     if(x==T) return f;
     int tp,used=;
     for(int i=head[x]; i; i=nxt[i]) {
         if(h[to[i]]==h[x]+&&val[i]) {
             tp=dfs(to[i],min(f-used,val[i]));
             val[i]-=tp;
             val[i^]+=tp;
             used+=tp;
             if(used==f) return f;
         }
     }
     if(!used ) h[x]=-;
     return used;
 }
 int maxflow;
 void dinic() {
     maxflow=;
     while(bfs()) {
         maxflow+=dfs(,inf);
     }
 }
 int main() {
     int x;
     cin>>n>>m;
     T=n*m;
     for(int i=; i<=n; i++) {
         for(int j=; j<m; j++) {
             scanf("%d",&x);
             ins(m*(i-)+j,m*(i-)+j+,x);//建图过程。加的反边也应权为x，因为反向也可能跑兔子。
         }
     }
     for(int i=; i<n; i++) {
         for(int j=; j<=m; j++) {
             scanf("%d",&x);
             ins(m*(i-)+j,m*(i)+j,x);
         }
     }
     for(int i=; i<n; i++) {
         for(int j=; j<m; j++) {
             scanf("%d",&x);
             ins(m*(i-)+j,m*(i)+j+,x);
         }
     }
     dinic();
     cout<<maxflow;
     return ;
 }