题解 洛谷 P4047 【[JSOI2010]部落划分】

我觉得几乎就是一道最小生成树模板啊...

题解里许多大佬都说选第n-k+1条边，可我觉得要这么讲比较容易理解

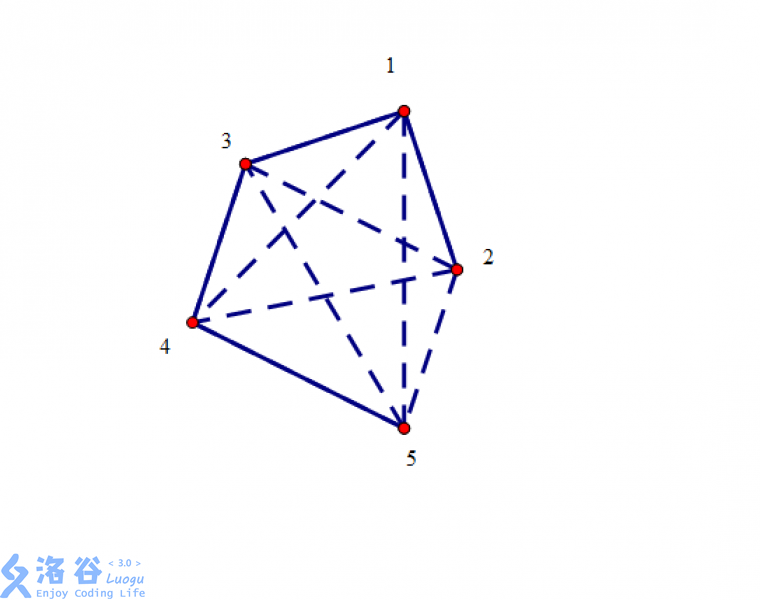
(虚边为能选的边，实边为最小生成树)

令n=5,k=2,(1,3)<(1,2)<(3,4)<(4,5)（PS:(4,5)<(2,5)，图画错了，见谅）

然后开始分部落（被同一个三角形套住的为一个部落的）：

(1)

这样肯定不为最优部落划分，因为他们的距离为(1,3)

(2)

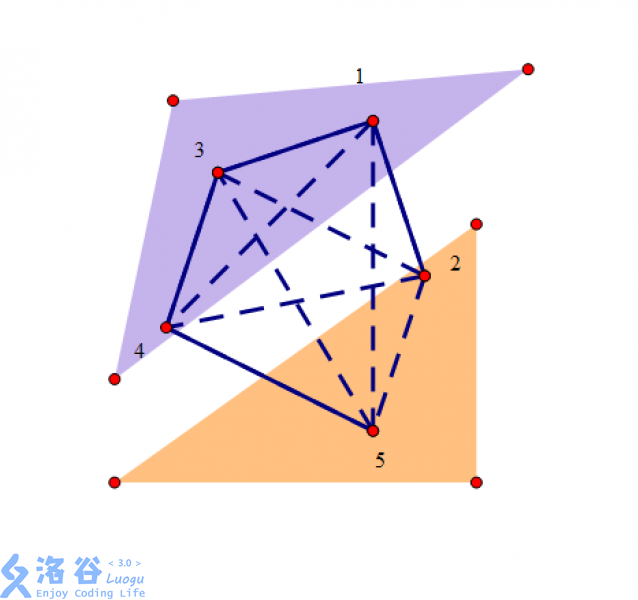
同理，这样也不行

(3)

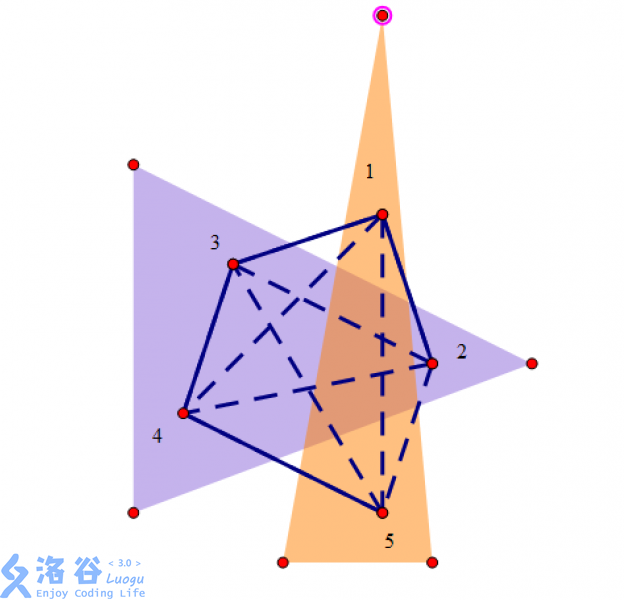
这样当然是不行的

所以，我们得出了这样一个结论：

要尽量选大边

所以小边要尽量在一个部落里，即下图：

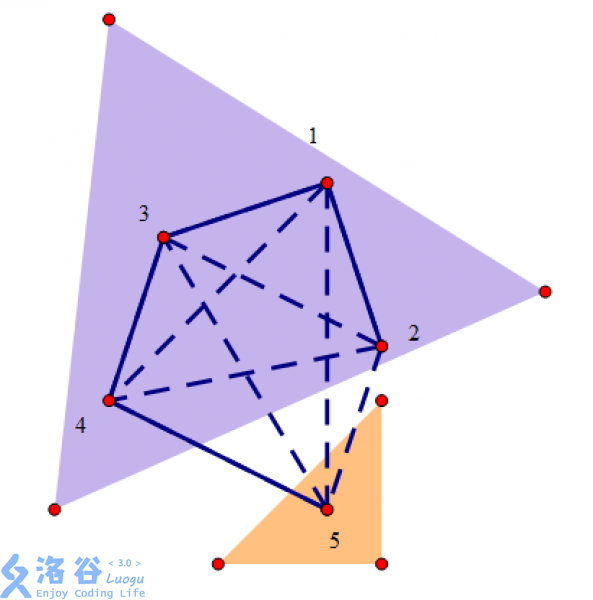
又因为有k个部落，所以可以消掉(n-1)-(k-1)条边，所以最小的为第n-k+1条边，所以就输出a[n-k+1]

代码如下：

#include<cstdio>
#include<algorithm>
#include<cmath>
using namespace std;
inline int read(){
    int r=,f=;
    char c=getchar();
    while(c<''||c>''){if(c=='-')f=-,c=getchar();}
    while(c>=''&&c<='')r=(r<<)+(r<<)+c-'',c=getchar();
    return r*f;
}
struct E{
    int u,v;
    double dis;//记得为double
}e[];
int f[],s_e,n,m;
int find(int x){
    if(f[x]!=x)f[x]=find(f[x]);
    return f[x];
}
inline bool cmp(E a,E b){
    return a.dis<b.dis;
}
double a[];//记得为double
int x[],y[];
int main(){
    n=read(),m=read();
    for(int i=;i<=n;i++)f[i]=i,x[i]=read(),y[i]=read();
    for(int i=;i<=n;i++)
        for(int j=;j<i;j++){
            s_e++;
            e[s_e].u=i;
            e[s_e].v=j;
            e[s_e].dis=(double)sqrt((x[i]-x[j])*(x[i]-x[j])+(y[i]-y[j])*(y[i]-y[j]));//计算sqrt((x1-x2)^2+(y1-y2)^2)，即距离
        }
    sort(e+,e++s_e,cmp);//最小生成树
    int i=;
    int j=;
    while(j<n-){
        int fu=find(e[i].u),fv=find(e[i].v);
        double dis=e[i].dis;//记得为double
        if(fu!=fv){
            f[fu]=fv;
            j++;
            a[j]=dis;//记得为double
        }
        i++;
    }
    printf("%.2lf",a[n-m+]);//记得是小数点后两位两位
    return ;
}